XiaoMi-AI文件搜索系统
World File Search System迪斯科舞厅:增强具有离散潜在潜在的连续扩散模型
扩散模型(DMS)已彻底改变了一般学习。他们利用扩散过程将数据编码为简单的高斯分布。但是,将复杂的,潜在的多模式数据分布编码为单个连续的高斯分布可以说是一个不必要的挑战性学习问题。我们建议通过引入互补的离散la-Tent变量来简化此任务,以简化此任务。我们使用可学习的离散潜在潜在的DMS增强DM,并用编码器推断出DM和DM和编码器端到端。Disco-Diff不依赖于预训练的网络,因此该框架普遍适用。离散的潜伏期可以通过降低DM生成ode的曲率来大大简化学习DM的复杂噪声到数据映射。加法自动回归变压器模型离散潜伏期的分配,这是一个简单的步骤,因为迪斯科舞厅只需要很少有带有小型代码的离散变量。我们在玩具数据,几个图像合成任务以及分子对接方面验证了DISCO-DIFF,并发现引入离散潜在潜伏期始终可以改善模型性能。例如,Disco-Diff在具有ODE Sampler的类调节Imagenet-64/128数据集上获得了最先进的FID分数。
可证明且实用的:通过Langevin Monte Carlo
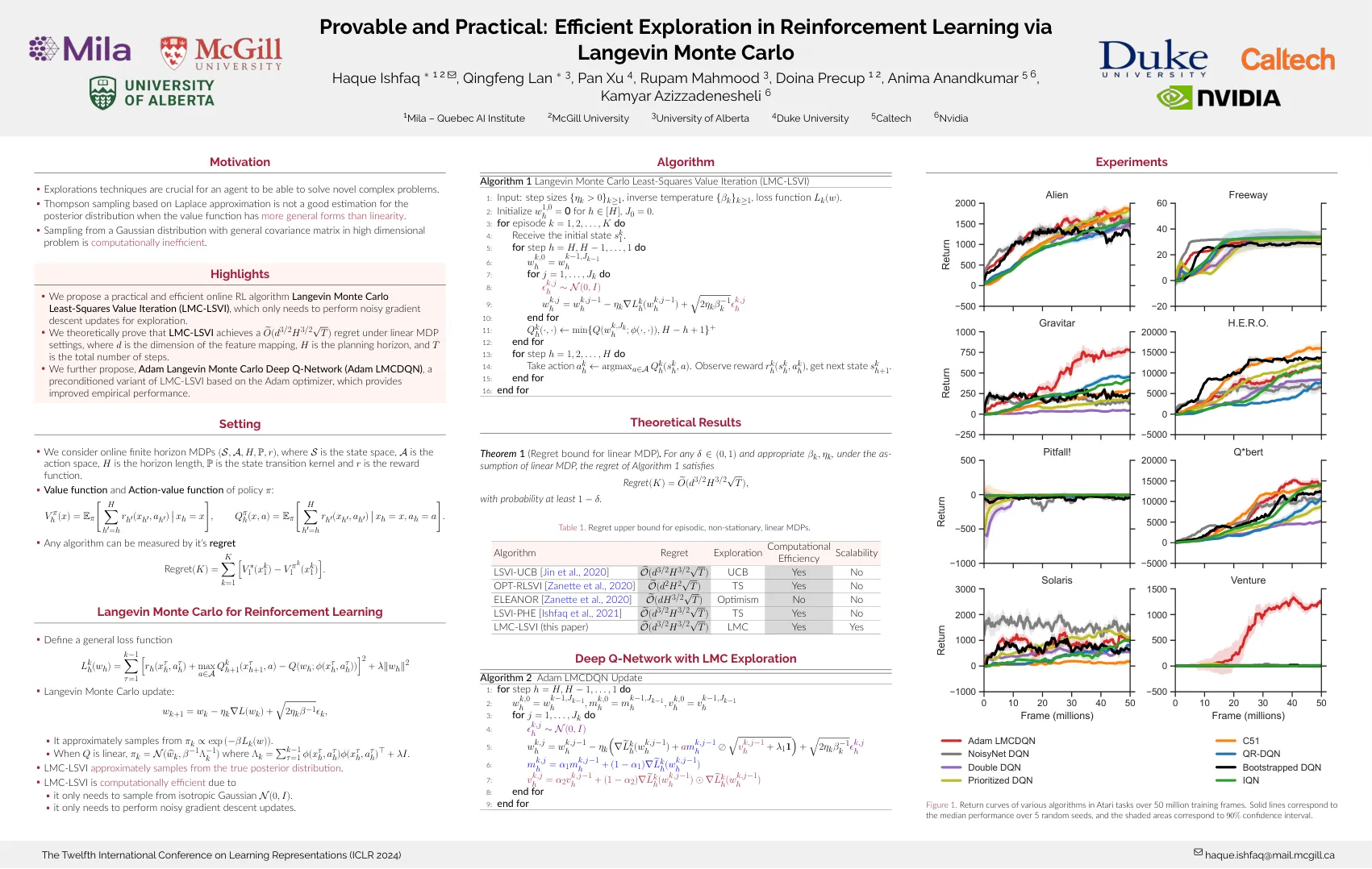
探索技术对于能够解决新的复杂问题的代理至关重要。基于拉普拉斯近似的汤普森采样是当值函数比线性更一般形式时,对后验分布不是一个很好的估计。在高维问题中具有一般协方差矩阵的高斯分布的采样在计算上效率低下。
SUS GAUSSIAN分布及其...
我们证明存在一个通用常数c> 0,因此对于每个d∈N,r d上的每个cen subgaussian分布d,每个偶数偶数p∈N,d variate polyenmial(cp)p/ 2·p/ 2·v v v∥p 2 - e x〜d -e x〜d〜d〜d v,x〜v,x〜v,x〜v,x〜v,x〜v,x〜是平方polynoms of Square polynoms of Square polynoms sum s sum s sum sarear polynoms s。这表明每个次高斯分布都是SOS信誉的次高斯 - 这种条件可为各种高维统计任务提供有效的学习算法。作为直接的推色,我们在计算上有效算法,并为以下任务提供几乎最佳的保证,当给定任意次高斯分布的样品时,我们可以遵守均值估计,可列表的均值均值估计,均值分离的均值混合模型,可靠的均值估计,可靠的估计量,强大的估计,可强大的估计,估算强大的估计,估算。我们的证明是对Talagrand的通用链接/主要措施定理的必要利用。
SIGE HBT晶体管选定参数的优化
过去几年已经看到了SIGE异质结双极晶体管(HBT)技术的显着进步。今天,Sige-Base HBTS的使用越来越多地在无线和高速数字通信中流行。在这些晶体管中,带隙分级产生了一个漂移场,这有助于少数载体通过基座运输。这一事实已被用来实现具有高切割频率F t(超过100 GHz)的设备。在文献[1-5]中广泛研究了SIGE HBTS中的基本运输时间的GE PROFE和BASE掺杂量的设计。三角形的ge profle在优化底座中的带隙分级有效,以最大程度地减少t b sige(基本运输时间 - f t中的主要因素)。由于已经检查了指数碱基的掺杂掺杂率和类似的基础[4,5],我们的目的是对底座中掺杂剂的高斯分布进行处理。在常规设备中,这种分布导致基本运输时间降低[6],因此估计其对SIGE HBT的影响是有用的。此外,在实际晶体管中,掺杂填充物比高斯分布更接近于指数。对SIGE HBT的两个重要参数进行了建模,即基本运输时间和当前增益。模型不仅是高掺杂效应的,而且还依赖于di usion系数的依赖性对漂移轨道和沿基数的可变GE浓度。基础中的两种类型的GE分布进行了检查:三角形的一个和框一[4,7]。
对激光束能曲线的模拟和实验分析,以提高线馈激光沉积的效率
抽象的激光覆层是一项公认的技术,大多数先前的数值建模工作都集中在基于粉末过程的过程中的交付和融化池行为。这项研究对优化的激光束成型进行了新的研究,以针对电线基的独特特性,其中直接底物加热以及电线和底物之间的热传递非常重要。与基于粉末的材料交付相比,该主题的值是通过基于电线的沉积过程来改善的沉积速率和致密的金属结构。线内温度分布(AISI 316不锈钢),底物的传热和直接加热(低碳钢)是通过传热模拟建模的,具有三个激光束辐照度分布。此分析确定了通常与标准高斯分布相关的局部高温区域的去除,以及均匀方形梁曲线可以提供的改进的底物加热。使用横截面光学显微镜分析了使用预位线和1.2 kW CO 2激光器的实验,以提供模型验证和改进的电线覆盖层润湿的证据,同时维持甲壳材料中有良好的抗甲基甲虫。这项工作的关键发现是从480 W/mm 2减少,在从高斯分布更改为均匀的平方分布时,需要辐照辐射,以进行有效的熔融池形成。这也可减少总能量50%。认可和讨论了能源效率,降低成本和可持续性改善的潜在提高。
通过 ACM 模型实现低功耗 CMOS 差分放大器
摘要 — 统计技术经常用于预测电子系统的性能。工艺变化考虑了制造时材料参数的不确定性,会对模拟集成电路的产量产生不利影响。对由于制造参数变化而导致的模拟电路关键输出参数变化进行统计分析,以预测产量,是模拟芯片制造中必不可少的步骤。在这项工作中,我们使用严格的统计方法来检查典型模拟电路的性能。我们设计了一个 65 nm 技术的两级 CMOS 差分放大器配置,使用 ACM 模型参数来检查工艺变化下的产量。我们采用三种不同的蒙特卡罗模型(均匀、高斯、最坏情况)来检查设计的 CMOS 差分放大器关键性能参数的统计变化。据报道,在典型工艺参数变化 10% 的情况下,关键差分放大器参数、最大增益、增益裕度和相位裕度都会发生变化。在最坏情况分布的情况下,变化最大,而在高斯分布的情况下,变化最小。结果表明,工艺变异对设计的CMOS差分放大器的成品率有显著影响。在高斯分布的情况下,增益裕度(dB)、相位裕度(度)和最大增益(dB)的标准差分别为11、25和24。
在 Bures-Wasserstein 流形上取平均值:维度——……
我们研究了用于计算高斯分布重心的关于最优传输度量的一阶优化算法。尽管目标是测地非凸的,但黎曼 GD 经验上收敛速度很快,实际上比欧几里德 GD 和 SDP 求解器等现成方法更快。这与黎曼 GD 最著名的理论结果形成了鲜明对比,后者与维度呈指数相关。在这项工作中,我们在辅助函数上证明了新的测地凸性结果;这为黎曼 GD 迭代提供了强大的控制,最终产生了无维度的收敛速度。我们的技术还可以分析两个相关的平均概念,即熵正则化的重心和几何中位数,为这些问题的黎曼 GD 提供了第一个收敛保证。
水和废水检验的标准方法
会随机分布在平均值 (算术平均值) 附近。如果累积无数次这样的测量,各个值将分布在类似于图 1010:1 所示的曲线中。左侧曲线表示高斯分布或正态分布,可以用平均值 µ 和标准差 σ 精确描述。分布的平均值或平均值就是所有值的总和除以求和的值的数量,即 µ = ( ∑ i x i )/ n 。因为没有测量会重复无限次,所以使用相同的求和程序,但 n 等于有限次重复测量 (10、20 或...),对平均值进行估算。µ 的这个估计值用 x 表示。正态分布的标准差定义为 σ = [ ∑ ( x −µ ) 2 / n ] 1/2 。同样,由于观测次数有限,分析师只能估计标准差;σ 的估计值用 s 表示,计算如下: