XiaoMi-AI文件搜索系统
World File Search SystemBrillouin
高速相干光子随机记忆在持久的声波中
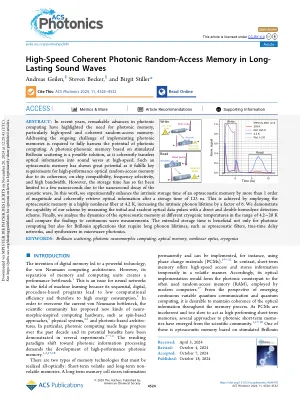
摘要：近年来，光子计算的显着进步突显了需要光子记忆，尤其是高速和连贯的随机记忆。应对实施光子记忆的持续挑战才能充分利用光子计算的潜力。基于刺激的布里鲁因散射的光子传声记忆是一种可能的解决方案，因为它一致地将光学信息传递到高速下的声波中。这样的光声内存具有巨大的潜力，因为它满足了高性能光随机记忆的关键要求，因为它的相干性，芯片兼容性，频率选择性和高带宽。但是，由于声波的纳秒衰减，到目前为止，迄今为止的存储时间仅限于几纳秒。在这项工作中，我们通过实验增强光声内存的固有存储时间超过1个数量级，并在存储时间为123 ns后连贯地检索光学信息。这是通过在4.2 K处高度非线性纤维中使用光声记忆来实现的，从而使内在的声子寿命增加了6倍。我们通过使用直接和双同性恋检测方案测量初始和读数光学数据脉冲来证明我们的方案能力。最后，我们分析了4.2 - 20 K范围内不同低温温度下光声记忆的动力学，并将发现与连续波测量值进行了比较。关键字：布里渊散射，光子神经形态计算，光学记忆，非线性光学，低温■简介延长的存储时间不仅对光子计算，而且对需要长声子寿命的Brillouin应用程序，例如光声过滤器，真实时延迟网络和微波光子学中的合成器。
抗铁磁体中的连贯的旋转动力学超越...
受控的具有最高频率和最短波长的相干旋转波是旋转和镁质的基石。在这里，使用Heisenberg Antiferromagnet RBMNF 3，我们证明激光诱导的Thz旋转动力学对应于对应于相互一致的反向传播波的成对，波向量到Brillouin区域的边缘，无法用磁性和抗模型（antiferromagnotic）旋转（nneellomagnetial）dictive（nneellomagnetial）。相反，我们建议使用自旋相关函数对这种自旋动力学进行建模。我们得出了后者的量子力学运动方程，并强调与磁化和抗磁磁性不同不同，抗铁磁体中的自旋相关性不表现出惯性。
二维柱状纳米粒子的密度泛函理论研究
图 1：单层结构，(ab) 碘化铅-PbI 2 ，(cd) 氧化铅 PbO ，(ef) 氧化锡 SnO ，(gh) 硫化铟-InS ，(ij) 硒化铟-InSe ，分别为顶视图和透视侧视图。(k) PbO 和 SnO ，(l) PbI 2 ，InS 和 InSe 的第一布里渊区路径。原子颜色代码：黑色=Pb，紫色=I，红色=O，浅蓝/灰色=Sn，浅粉色=In，黄色=S，绿色=Se
smtd.202001147.pdf
图 1. (a) 左图：具有 Pm3m 空间群的 MAPbI 3 立方晶体结构的 3D 视图。MA +（红球）位于立方体的中心，而 Pb 2+（灰球）被八面体中的 I -（紫球）包围。右图：显示 Pm3m 空间群的第一布里渊区 (BZ) 的 3D 视图。Γ 表示 BZ 的原点；X 是 BZ 边界处正方形面的中心；M 是立方体边缘的中心；Rs 是立方体的顶点。[8] (b) 电导率测量装置的示意图。大晶粒薄膜 (c)、小晶粒薄膜 (d) 和单晶 (e) 的温度相关电导率。[10]
量子力学和量子场中的 5 路径积分...
路径积分图景之所以重要，有两个原因。首先，它提供了量子力学的另一种补充图景，其中经典极限的作用显而易见。其次，它为研究微扰理论不充分或完全失效的领域提供了一条直接途径。在量子力学中，解决此类问题的标准方法是 Wentzel、Kramers 和 Brillouin 的 WKB 近似。然而，将 WKB 近似推广到量子场论是极其困难的（甚至是不可能的）。相反，费曼路径积分的非微扰处理（在量子力学中等同于 WKB）可以推广到量子场论中的非微扰问题。在本章中，我们将仅对玻色子系统（如标量场）使用路径积分。在后续章节中，我们还将对路径积分进行全面的讨论，包括它在费米子场、阿贝尔和非阿贝尔规范场、经典统计力学和非相对论多体系统中的应用。
在光子平带上的连续体中的超绑定状态
在这项工作中，我们从理论上提出并在实验上证明了在光子晶体平坦带上连续体（BIC）中的超结合状态的形成。这种独特的状态同时在布里渊区的扩展区域中表现出增强的质量因子和接近零组的速度。在拓扑转换时实现了对称性保护的BIC固定在K = 0与两个Friedrich-Wintgen Quasi-BICS合并，这是由相反对称性的有损光子模式之间的破坏性干扰引起的。作为概念验证，我们采用了Ultraflat Super BIC来证明单个颗粒的三维光学诱捕。我们的发现提出了一种新颖的方法，可以在次波长量表上为创新光电设备的次波长量表进行工程。
![arxiv：2501.18491v1 [cond-mat.mes-hall] 2025年1月30日](/simg/5\59e3d56f8650598cb67a5f8f2d30cac6f719b565.webp)
arxiv：2501.18491v1 [cond-mat.mes-hall] 2025年1月30日
在这里，我们提出了一种镜面对称魔术角扭曲三层石墨烯的理论。通过具有远距离隧道矩阵元素的哈伯德模型来描述电子特性。通过求解平均场哈伯德模型获得电子性能。我们获得具有特征性平坦带和狄拉克锥体的带结构。在电荷中立性时，打开电子电子相互作用会导致金属至抗磁相变，其Hubbard相互作用强度比其他石墨烯多层小得多。我们分析了抗铁磁状态的固定性对六角硼氮化物封装引起的对称破裂的性能，以及由将狄拉克锥与平面带混合的电场的应用引起的镜像破坏。此外，我们探索了系统的拓扑特性，揭示了隐藏的量子几何形状。尽管平坦的频带为零，但在MoiréBrillouin区域上的多型浆果曲率分布表现出非平凡的结构。最后，我们提出了一种调整此量子几何形状的机制，提供了控制系统拓扑特性的途径。
关于altermagnetism和超导性的注释
altermagnetism是最近发现的一种新型的共线磁铁，它与铁磁体共享某些特征（在Brillouin Zone的一般点上缺乏非同性化的Kramers退化性，有限的综合大厅的效果，有限的磁磁效应），另一种与Antiferromagagnets（net Magnetiza-tione symention sonefore效应）[1]。虽然已经探索了altermagnets的许多特性，这在很大程度上是从旋转的角度，超导二极管和altermagnetism之间的相互作用的角度，这是另一个方面，其中铁磁体和抗fiferromagnets主要不同的是，到目前为止尚未解决。毫不奇怪，Altermagnets可以在一种情况下表现出典型的铁磁体的属性，而在另一种情况下，抗fiferromagnets典型的属性。There are two issues that are typically considered in terms of interaction between magnetism and supercon- ductivity: (1) what kind of superconducting state may be consistent with a given magnetic order and (2) what kind of pairing can be generated by proximity to a mag- netic order (in other words, if we can gradually suppress the long range magnetic order by an external stimulus, such as pressure, what supperconducting symmetry may emerge on the量子的两侧？）。
PHYS3111 T2 2021 课程大纲
量子力学是现代物理学的基石，研究微观尺度上的物理现象。这是本科生量子力学的最高课程，将为学生提供广泛而全面的介绍和进一步学习的基础。涵盖的主题包括：三维量子力学。角动量。氢原子。朗道能级。自旋。全同粒子和自旋统计关系。克莱布希-戈登系数。时间无关的微扰理论及其应用：一维弱正弦势中的粒子动力学、能带结构、布洛赫定理、布里渊区、准动量、金属和能带绝缘体。时间相关微扰理论。费米黄金法则。绝热演化和贝里相。散射理论中的粒子波分析。玻恩近似散射振幅的色散关系。低能和共振散射。