XiaoMi-AI文件搜索系统
World File Search SystemKolmogorov
论量子失相过程的经典性
我们分析了纯失相系统相关的多时间统计数据，这些统计数据反复用尖锐测量探测，并寻找其统计数据满足 Kolmogorov 一致性条件（可能达到有限阶）的测量协议。我们发现了量子失相过程的丰富现象学，可以用经典术语来解释。特别是，如果底层失相过程是马尔可夫过程，我们会发现在每个阶上都可以找到经典性的充分条件：这可以通过选择完全兼容或完全不兼容的失相和测量基础（即相互无偏基 (MUB)）来实现。对于非马尔可夫过程，经典性只能在完全兼容的情况下证明，从而揭示了马尔可夫和非马尔可夫纯失相过程之间的一个关键区别。
迈向模拟模型复杂性测量 - AFIT Scholar
摘要：是否有可能开发出一种有意义的方法来衡量模拟模型的复杂性？算法信息论提供了已应用于其他研究领域的概念，用于实际测量对象复杂性。本文从多个角度概述了复杂性，并提供了有关模拟模型复杂性的知识体系。定义了模型细节、分辨率和范围等关键词。算法信息论中的一个重要概念——柯尔莫哥洛夫复杂性，以及该概念的一个应用——归一化压缩距离，用于表示测量模型细节变化的可能性。该领域的进一步研究可以推动建模和仿真知识体系向测量模拟模型复杂性的实际应用迈进。示例表明，模拟模型的 KC 和 NCD 测量可以检测到范围和细节的变化。
Kahoot! 在医学教育中的应用
世界各地都在努力将技术应用于医学教育，以提高大班学生的学习积极性。Kahoot! 就是其中之一。本研究旨在测量 FKIK UMY 医学院在实施 Kahoot! 后学生的学习积极性水平。本研究采用了准实验方法。数据是使用学习动机策略问卷 (MSLQ) 收集的。在使用 Kolmogorov Smirnov 方法进行正态性检验时，所有数据的 p 值均大于 0.05。因此，我们使用非参数分析和独立样本 T 检验以及单因素方差分析来找出学生成绩与学生学习积极性水平之间的关系。研究结果表明，2015 年级学生在实施 Kahoot! 后学习积极性水平较低，其他三个年级（2016、2017 和 2018）在实施 Kahoot! 后学习积极性水平较高。执行此操作的技术人员将在本次培训中获得相关动机。 Salah satunya adalah Kahoot！ Penelitian ini bertujuan untuk mengukur tingkat motivasi mahasiswa fakultas kedokteran FKIK UMY pasca Implementasi Kahoot!. Penelitian ini menggunakan metode eksperimen semu.学习动机策略问卷 (MSLQ) 的数据。宇治正常情况下，柯尔莫哥洛夫·斯米尔诺夫·斯米尔诺夫·斯米尔诺夫·斯米尔诺夫·斯米尔诺夫·斯米尔诺夫·斯米尔诺夫·斯米尔诺夫·斯米尔诺夫·斯穆阿·塞穆阿数据memiliki nilai p> 0,05。 Dengan demikian、analisis statistic menggunakan non-parametrik dengan 独立样本 T 检验和单向方差分析 untuk mengetahui hubungan nilai siswa dan tingkat motivasi siswa。 Hasil penelitian menunjukkan bahwa mahasiswa angkatan 2015 memiliki tingkat motivasi yang lebih rendah setelah penerapan Kahoot!, tiga kelas lainnya (2016, 2017, dan 2018) memiliki tingkat motivasi yang lebih tinggi setelah penerapan Kahoot!。
EEG信号处理 20世纪欧洲的经济历史 艾森豪威尔与冷战经济
2.6连贯性，多元自回归（MVAR）建模和定向转移功能（DTF）67 2.7混乱和动态分析71 2.7.1熵71 2.7.2 Kolmogorov熵71 2.7.7.3.7.3 Series 75 2.7.6 Approximate Entropy 11 2.7.7 Using the Prediction Order 78 2.8 Filtering and Denoising 79 2.9 Principal Component Analysis 83 2.9.1 Singular-Value Decomposition 84 2.10 Independent Component Analysis 86 2.10.1 Instantaneous BSS 90 2.10.2 Convolutive BSS 95 2.10.3 Sparse Component Analysis 98 2.10.4 Nonlinear BSS 99 2.10.5 Constrained BSS 100 2.11受约束BSS的应用：示例102 2.12信号参数估计104 2.13分类算法105 2.13.1支持向量机106 2.13.2 K-Means算法114 2.14匹配匹配追踪117 2.15摘要和结论118参考119 119 119
识别马耳他患糖尿病前期和糖尿病风险较高的年轻人：一项横断面调查
本研究的目的是量化年轻人中糖尿病前期的风险和相关风险因素。我们还试图评估所用风险评估工具的有效性和可靠性。还收集了空腹血糖以进一步评估风险。进行了一项横断面相关性研究。采用便利抽样，目标样本量为 374。在总共 14,483 名符合条件的参与者中，176 名（回复率 = 1.22%）就读于两所高等教育机构的 18-35 岁年轻人的数据收集时间为 2020 年 12 月 22 日至 2021 年 4 月 30 日。使用在线问卷，包括对 57 名参与者进行空腹血糖测试。分析使用 IBM® SPSS® Statistics Version 27。Kolmogorov–Smirnov 和 Shapiro–Wilk 检验、Mann–Whitney U 检验、Pearson 和 Spearman 相关性、Fisher 精确检验、单变量一般线性模型和受试者工作特征分析均用于分析数据。5.3% (n=3) 的参与者，他们
熵经济：人工智能时代的碳减排和能源效率新范式
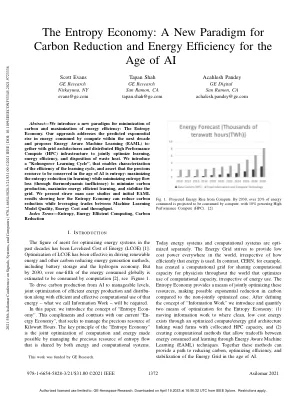
摘要 — 我们引入了一种最小化碳排放和最大化能源效率的新范式：熵经济。我们的方法解决了未来十年内计算消耗的能源预计呈指数增长的问题，并提出了能源感知机器学习 (EAML) 与网格架构和分布式高性能计算 (HPC) 基础设施，以共同优化学习、能源效率和废热处理。我们引入了一个“Kolmogorov 学习循环”，可以表征学习循环的效率，并断言人工智能时代要节约的宝贵资源是熵：最大化熵减少（在学习中）同时最小化熵流损失（通过热力学效率低下）以最大限度地减少碳排放，最大限度地提高节能学习，并稳定电网。我们提出了稻草人案例研究和初步的 EAML 结果，展示了熵经济如何在利用机器学习模型质量、能源成本和吞吐量之间的权衡的同时减少碳排放。索引术语 — 熵、节能计算、碳减排
稳定驱动的McKean-Vlasov Sdes
摘要。我们考虑了一般的McKean-Vlasov随机分化方程，该方程是由旋转变体α-稳定过程驱动的，α∈（1，2）。我们假设分支系数是身份矩阵，并且漂移是有界的，并且在某种意义上，相对于空间和测量变量，Hölder是连续的。这项工作的主要目标是证明相关均值相互作用粒子系统的混乱估计值的新弱传播。我们还对一个粒子的密度与限制麦基恩 - 维拉索夫SDE的密度之间的差异建立了一个重点控制。我们的研究依赖于与麦凯恩·维拉索夫（McKean-Vlasov）随机差异方程相关的正规化支持和半群的动力学，该方程的作用于在pβ（r d）上定义的函数，概率的空间在r d上具有r d的概率测量空间。更准确地说，半群的动力学是由在条[0，t]×pβ（r d）上定义的向后的kolmogorov偏差方程来描述的。
mepsi：一种基于MDL的合奏修剪方法，具有结构信息
合奏修剪结合了并行制作预测产生的个体学习者的子集是整体学习中的重要话题。过去几十年来开发了许多修剪算法，这些算法的重点是学习者对样本的外部行为，这可能会导致过度拟合。在本文中，我们猜测合奏的概括性能不仅与样本上的外部行为有关，而且还取决于分裂学习者的内部结构。我们提出了基于kolmogorov复杂性和最小描述长度（MDL）原理的一般MEPSI方法，该原理制定了综合修剪任务，作为构成两种目标的优化问题，这些问题包括个人学习者之间的经验误差和结构信息。我们还提供了对决策树的MEPSI的具体实现。理论结果为一般的MEPSI方法和基于树的实现提供了概括。在多个现实世界数据集上进行的合规实验证明了我们提出的方法的有效性。
![arxiv：2408.05121v1 [Math.lo] 2024年8月9日](/simg/g:\will\search\icon\source\b\b469870291268fde986c2ee4fcc0d09b86159734.webp)
arxiv：2408.05121v1 [Math.lo] 2024年8月9日
从Ryabko [41，41]和Staiger [47，48，49]的作品开始，在过去的30年中，研究人员研究了分类维度与算法信息理论之间的密切关系。在此关系的中心是hausdor效率的点版本（由于lutz [29，30]），也就是说，一个维度的概念是为空间中的单个点而不是子集中的单个点定义的概念。这是通过影响度量的概念（从Martin-Löf[33]的意义上）来实现的，该概念限制了无数零食的收集到一个可数家族，从而使Singleton集合不可以null。在此框架中，此类单例被认为是随机的。随机性与kolmogorov复杂性的各种瞬态（算法随机性理论的基石）之间的对应关系，然后以渐近信息密度的形式重新出现，与平稳过程的熵非常相似。有效的维度使许多作者发掘了熵和分形维度之间的连接（可以说是从Billingsley [2]和
算法信息理论的统计机械解释
算法信息理论是将信息理论和概率思想应用于递归功能理论的框架。算法信息理论的主要概念之一是有限的二进制字符串s的程序大小复杂性（或kolmogorov复杂性）h（s），它定义为通用自我自我阐述的杜松疲劳的最短二进制程序的长度。根据定义，可以将h（s）视为单个有限二进制字符串s的信息内容。实际上，算法信息理论正是经典信息理论的形式特性（参见Chaitin [3]）。程序大小复杂性的概念在表征有限或有限的二进制字符串的随机性方面起着至关重要的作用。在[3]中，Chaitin引入了停止概率ω，作为有限二进制字符串的随机示例。他的ω被定义为通用自我启动的图灵机U停止的概率，并且在算法 - MIC信息理论的当数学发展中起着核心作用。ω的基础两个膨胀的第一位解决方案，解决了一个不大于n的程序的停止问题。通过此属性，ω的基础两张扩展显示为有限的二进制字符串。在[7，8]中，我们通过