XiaoMi-AI文件搜索系统
World File Search System纳西拉巴德 (RAJ) 陆军公立学校
4.有意向且符合条件的候选人可通过学校网站 www.apsnasirabad.in 提供的申请表申请,同时附上所有证书的自认证副本和 250 卢比的手续费(不可退还),以汇票形式支付给 Nasirabad 陆军公立学校校长。申请应于 2025 年 1 月 25 日或之前送达 Nasirabad (Rajasthan) 陆军公立学校校长,P-191 The Mall,PIN – 305601。不接受通过电子邮件提交的申请。仅接受纸质申请表,可亲自/邮寄。本机构不对任何邮件延误负责。学校保留填补上述任何职位或不填补任何职位的权利。学校管理部门的决定将具有最终决定权。
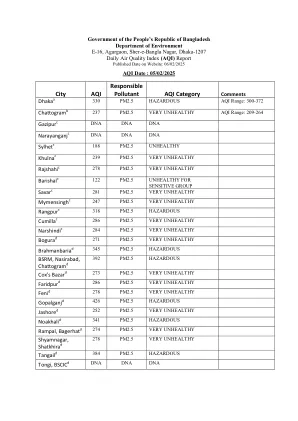
城市AQI负责任的污染物AQI类别
Barishal C 122 PM2.5 Sensew不健康Narshindi C 284 PM2.5非常不健康的Bogura D 271 PM2.5非常不健康的Brahmanbaria D 345 PM2.5危险BSRM,Nasirabad,Chattogram D
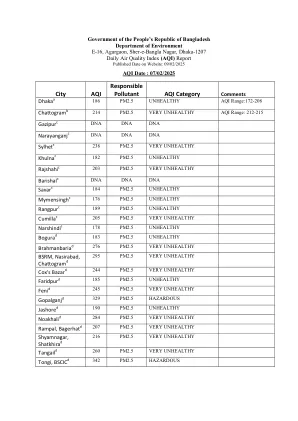
城市 AQI 主要污染物 AQI 等级
Barishal c DNA DNA DNA Savar c 184 PM2.5 不健康 Mymensingh c 176 PM2.5 不健康 Rangpur c 189 PM2.5 不健康 Cumilla c 205 PM2.5 非常不健康 Narshindi c 178 PM2.5 不健康 Bogura d 183 PM2.5 不健康 Brahmanbaria d 276 PM2.5 非常不健康 BSRM, Nasirabad, Chattogram d
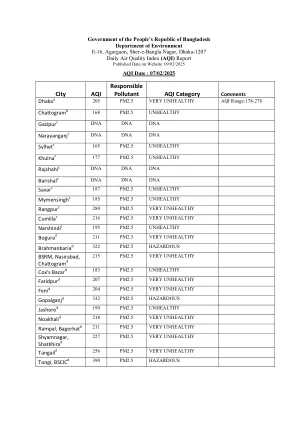
城市AQI负责任的污染物AQI类别
Barishal C DNA DNA SAVAR C 187 PM2.5不健康的Mymensingh C 185 PM2.5不健康的Rangpur C 280 PM2.5非常不健康的Cumilla C 216 PM2.5非常不健康的Narshindi C 195 PM2.5 PM2.5 PM2.5 Bogura
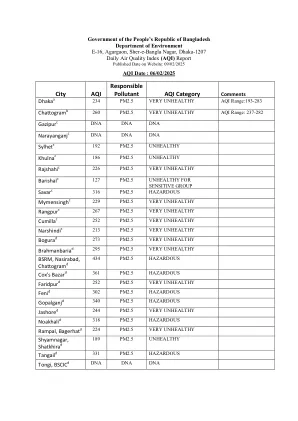
城市 AQI 主要污染物 AQI 等级
Barishal c 127 PM2.5 对敏感人群不健康 Savar c 316 PM2.5 有害 Mymensingh c 229 PM2.5 非常不健康 Rangpur c 267 PM2.5 非常不健康 Cumilla c 252 PM2.5 非常不健康 Narshindi c 213 PM2.5 非常不健康 Bogura d 273 PM2.5 非常不健康 Brahmanbaria d 295 PM2.5 非常不健康 BSRM, Nasirabad, Chattogram d
吠陀数学在计算机科学中的应用
Ravi Prakash Mathur博士数学系,S。G。S. G.政府学院,纳西拉巴德(印度)摘要:古代智慧与现代计算的融合是本研究论文中探讨的有趣的边界,该论文研究了吠陀数学在计算机科学领域的潜在应用。吠陀数学源自古老的印度文本,称为吠陀经,为数学问题提供了独特的方法 - 解决强调心理敏捷性,模式识别和优雅算法的方法。本文深入研究了吠陀数学的历史背景,追踪其起源和关键原则,并强调了其在当代计算机科学中的相关性。吠陀数学和计算机科学的交集通过识别共同原则(例如模式识别和优化)来照亮。本文探讨了具有提高计算效率的特定吠陀数学技术,包括减法的“ Nikhilam”方法以及用于乘法的“垂直和横向和横向”方法。案例研究以证明吠陀数学技术在计算机科学中的实际应用,跨越了数据处理,算法优化以及错误检测和校正等领域。但是,这种整合并非没有其挑战和道德考虑。本文解决了对准确性和可靠性的担忧,尤其是在将非常规数学技术整合到现代计算范式中时。文化敏感性和对吠陀数学起源的适当认可至关重要,需要确保多元化受众可以使用这些技术。还探索了交叉知识交流的道德意义,强调了协作和尊重的重要性。展望未来,本文概述了计算机科学教育的潜在研究方向和影响。吠陀数学的整合为开发新算法,增强问题的技能和培养跨文化理解提供了机会。数学家与计算机科学家之间的合作被强调为算法设计创新的有前途的途径。总而言之,吠陀数学和计算机科学的融合代表了古代传统和现代进步的动态相互作用。当我们浏览集成的复杂性时,我们踏上了超越学科界限,促进文化欣赏的旅程,并具有在数字时代重塑计算方法的潜力。关键字:吠陀数学,计算机科学,算法优化,模式识别,文化敏感性,交叉 - 学科整合1.简介吠陀数学是一种源自印度次大陆的古代数学技术系统,它引起了人们的关注,因为其出色的计算效率和优雅的问题 - 解决方法 - 解决方法。我们都非常了解教育方法的不断发展以及各种教学方法的重要性。在计算机科学领域,数学原理的整合是必不可少的,因为它是算法,数据结构和计算建模的基础。本文探讨了吠陀数学与计算机科学之间的引人入胜的交集,阐明了通过使这些看似不同的学科合并而产生的潜在应用和收益。对吠陀数学的研究将其根源追溯到吠陀经,这是古老的印度文本,这些文本封装了知识的各个方面,包括数学。这些数学技术被保留并传递到世代相传,促进了与常规方法不同的独特系统,但通常会产生相同的结果,尽管更有效。计算机科学是基于逻辑,算法和数学原理的现代领域,它共同为我们所居住的数字时代提供了掌控。这两个领域之间的相互作用是吠陀数学提高计算效率的有趣潜力,问题 - 解决速度,