XiaoMi-AI文件搜索系统
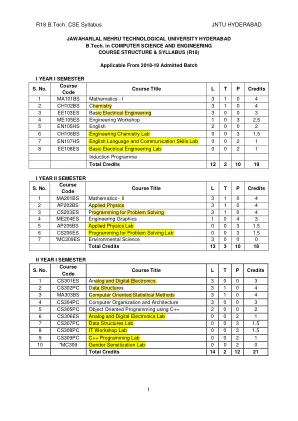
World File Search SystemR18 B.Tech。 CSE教学大纲Jntu Hyderabad 1R18 B.Tech。 CSE教学大纲Jntu Hyderabad 1
S.课程代码课程标题1专业选举 - V 3 0 0 3 2专业选举 - vi 3 0 3 3 3开放选修课-III 3 0 3 4 0 3 4 EC801PC项目阶段 - II 0 0 14 7总数9 0 14 16 *MC-环境科学应仅由横向入学学生注册。*MC - 令人满意/不令人满意的注意:以工业为导向的迷你项目/暑期实习应在暑假第六和第七学期之间进行。学生应提交面向工业的迷你项目/暑期实习的报告进行评估。专业选修课 - i
查看报告 - 为什么che@iith -iit hyderabad
1有关矿物质关键评估的更详细讨论,请参见Whittle,D.,M。Yellishetty,S。D。Walsh,G。Mudd和Z. Weng(2020)。矿物质批判性评估。Alta 2020铀和REE会议。 A. Taylor。 珀斯。Alta 2020铀和REE会议。A. Taylor。 珀斯。A. Taylor。珀斯。
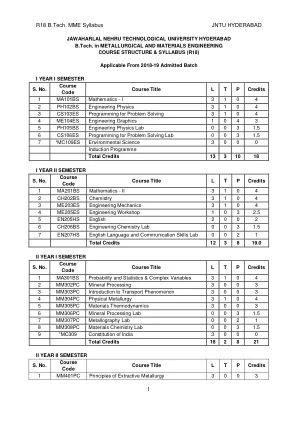
R18 B.Tech。 MME教学大纲Jntu Hyderabad 1
编写一组线性方程的矩阵表示,并分析方程系统的解决方案查找特征值和特征向量使用正交转换将二次形式减少到规范形式。在平均值定理上求解应用程序。使用beta和伽马函数评估不正确的积分找到两个具有/没有约束的变量的功能的极端值。评估多个积分,并将概念应用到查找区域,量ITUME-I:矩阵10 L矩阵的矩阵等级和正常形式的矩阵等级,正常形式,与juss-jordan方法的非单明性矩阵相反,高斯 - jordan方法,线性方程系统:均匀和非同性方程式的求解系统和非良好方程式的求解方法。UNIT-II: Eigen values and Eigen vectors 10 L Linear Transformation and Orthogonal Transformation: Eigenvalues, Eigenvectors and their properties, Diagonalization of a matrix, Cayley-Hamilton Theorem (without proof), finding inverse and power of a matrix by Cayley-Hamilton Theorem, Quadratic forms and Nature of the Quadratic Forms, Reduction of正交转换通过正交转换到规格形式的二次形式。单位-III:微积分10 L平均值定理:Rolle的定理,Lagrange的平均值定理,其几何解释和应用,Cauchy的平均值定理,Taylor的序列。确定积分的应用在评估曲线旋转的表面区域和体积(仅在笛卡尔坐标中),不当积分的定义:beta和伽马功能及其应用。单元IV:多变量演算(部分分化和应用)10 L极限和连续性的定义。部分分化:Euler的定理,总导数,Jacobian,功能依赖性和独立性。应用程序:使用拉格朗日乘数方法的两个变量和三个变量的功能的最大值和最小值。
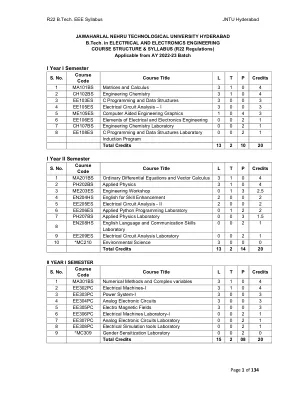
M.Tech控制工程 /控制系统< / div>
编写一组线性方程的矩阵表示,并分析方程系统的解决方案查找特征值和本征媒介使用正交转换将二次形式减少到规范形式。分析序列和序列的性质。在平均值定理上求解应用程序。使用beta和伽马函数评估不正确的积分找到两个具有/没有约束的变量的功能的极端值。单元I:矩阵矩阵:矩阵的类型,对称;隐士偏度对称;偏斜;正交矩阵;单一矩阵;按梯形形式和正常形式的矩阵等级,高斯 - 约旦方法的非单个矩阵倒数;线性方程系统;解决同质和非均匀方程的求解系统。高斯消除方法;高斯Seidel迭代方法。单元-II:特征值和本征载体线性变换和正交转换:特征值和特征向量及其特性:矩阵的对角线化; Cayley-Hamilton定理(没有证据);查找矩阵的逆向和力量由Cayley-Hamilton定理进行;二次形式的二次形式和性质;通过正交转换单位-III将二次形式的形式降低至规范形式:序列与串联序列:序列的定义,极限;收敛,发散和振荡序列。系列:收敛,发散和振荡系列;一系列积极术语;比较测试,p检验,D-Alembert的比率测试; Raabe的测试;库奇的整体测试;库奇的根测试;对数测试。泰勒的系列。交替系列:Leibnitz测试;交替收敛序列:绝对和有条件收敛。单元-IV:微积分平均值定理:Rolle的定理,Lagrange的平均值定理,其几何解释和应用,Cauchy的平均值定理。
野生动植物取证中的DNA技术(动物) - 海得拉巴
-Rakesh Mishra董事,CSIR -CCMB非法野生动植物贸易是全球威胁。在发展中国家,有标志性物种,例如老虎,亚洲大象,单角犀牛。定期将一些新的野生动植物物品包括在非法野生动植物贸易中。穿衣尺度,红色沙纸上,巨型盖克和监测蜥蜴正在偷猎以灭绝其身体部位。这些项目是无法识别的,并且从这种材料中涉及的物种的鉴定极具挑战性。此处概述的协议是十年来测试,标准化和成功应用基于DNA的技术在野生动植物法医学诊断中的结果。如果此SOP之后是感兴趣的各方,则可以及时解决一些野生动植物犯罪。
在国家法律法庭海得拉巴替补席上 - 1
在19.04.2023列出此问题。先生vvsn raju先生提出,并指出,根据IA.no.281/2023中的命令,清算人的立场被排出。因此,SBI代表利益相关者委员会将继续进行此申请,并已指示他向SBI提交Vakalat。允许根据过程提交vakalat。在19.04.2023列出此事。SD/-SD/ - 成员(T)成员(J)
AL WARQA - 海得拉巴全站仪测量
AA ll WW aarrqqaa SSUURRVVEEYYEENNGGIIN NEEEERRIINNGG iissoonneeoofftthheel leeaaddiinggaannddmm oossttaaddvvaanncceed dssuurrvveeyyiinnggcc oommppaanniieessiinn UU nniitteedd AA rraabb EE mmiirraatteess。 。 WW iitthhiittssoorrggaan niizzaattiioonnooffpp rrooffeessssiioonnaal lppeerrssoonnnneell , , uupp - - ttoo - - ddaatteeaannddssttaat teeoofftthheeaarrttee qquuiippmmeennttssaan nddaapppplliiccaattii oonnssaannddpprreecci isseemmeethhooddooll ooggiiess,, wweeddeeddiiccaatteet tooddeelliivveerrqquu aalliittyysseerrvviic ceettoooouurrcclliiee nnttss。 。 AA ll WW aarrqqaa SS uurrvveeyyhhaassggoot taapprroovveennttrraa cckkrreeccoorrddooffu unnddeerrttaakkiinngg aannddeexxeeccuuttiin nggsseevveerraallllaa rrggeepprroojjeecctts stthhrroouugghhiittss ccoommmmiitttteeddaan nddeexxppeerriieenncc eeddtteeaamm . . MM oottiivvaatteedd / / DD rriivveennwwiitthhaar roobbuussttppeerrssuu aassiioonnttoossuuccc ceeeeddaannddaaccccoo mmpplliisshhbbeetttte err . . WW eehhaavveeddeeddiicca atteeddaannddsskkiill lleeddtteeaammccaappa abblleeooffpprroovvii ddiinggqquaaalliitty ywwoorrkkaannddmmeeee ttiinggtthheessttrri innggeennttaaiimmooff tthheecclliieennttss。 。 EE ssttaabblliisshheeddi 旅馆 MM aayy 2 2 0 0 0 0 1 1 , ,AA ll WW aarrqaahhaassbbeeeen nwwoorrkkiinggiinntt hheeffiieellddooffssu urrvveeyywwiitthhtthh eemmoossttrreeppuutta abblleeccoonnssuulltt aannttssiinncclluuddi innggggoovveerrnnmmee nnttaaggeenncciieessa并很快就开始了 UUAAEE 的建设。 。 WW iitthhoovveerr 1 1 5 5 yyeeaarrssiinntthheef fiieellddooffssuurrvv eeyy , , oouurrcoommppaannyyh haasscceemmeennttedd iittssrreeppuuttaatti ioonnooffqquaalliitt yywwoorrkkwwiitthhccl liieennttsstthhrroouu gghhoouurroonn - - ttiimmeeaannddaaccccu urraatteeddeelliivvee rraabblleessuussiinng goouurrmmoossttaaddvv aanncceeddaannddssoop phhiissttiiccaatteedd ssooffttwwaarreeaannd deeqquuiippmmeennttss 。 。我们的愿景
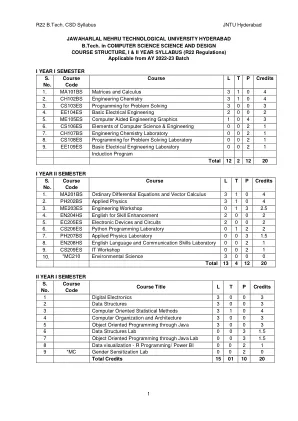
R22 B.Tech. CSD 教学大纲 JNTU 海得拉巴 1 ...
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 评估多重积分并应用概念来寻找面积和体积 UNIT - I:矩阵 10 L 通过梯形和标准形式对矩阵进行秩,通过高斯-乔丹方法对非奇异矩阵进行逆运算,线性方程组:用高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元:特征值和特征向量 10 L 线性变换和正交变换:特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理(无证明)、用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、用正交变换将二次型简化为标准形式。 第三单元:微积分 10 L 均值定理:罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积(仅限于笛卡尔坐标系)、不当积分的定义:Beta 函数和 Gamma 函数及其应用。第四单元:多元微积分(偏微分和应用)10 L 极限和连续性的定义。偏微分:欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用:使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
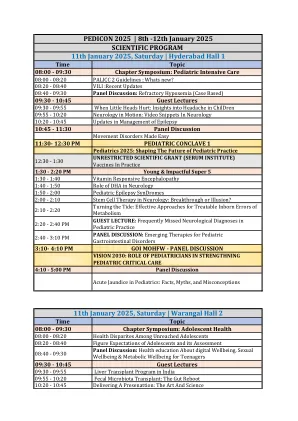
2025年1月11日,星期六|海得拉巴大厅1
Time Topic 08:00 - 09:30 Chapter Symposium: Infant & Young Child Feeding 08:00 - 08:20 New Insights into the Mastitis Spectrum 08:20 - 08:40 Colostrum: The White Gold 08:40 - 09:30 Panel Discussion: Human Milk Banking--Scopes and Horizons 09:30 - 10:45 Guest Lectures 09:30 - 09:55 Syncope Decoded 09:55 - 10:20 Approach to Pediatric hypertension 10:20 - 10:45 Rising to the Challenge: AdDressing Polio Resurgence 10:45 - 11:30 Panel Discussion Tele Echo: Bringing Cardiac Diagnostics to Your Doorstep 11:30- 12:30 PM Guest Lectures 11:30 - 12:00 Intriguing Case Scenarios In Pediatric Nephrology 12:00 - 12:30 The Fragile Filter: Preserving Kidney Function In Pediatric Patients 12:30 - 1:30 PM AWARD PAPERS 1:30 - 2:20 PM Young & Impactful Super 5 1:30 - 1:40 Echogenic Focus in Antenatal scan 1:40 - 1:50 Keeping the PDA open 1:50 - 2:00 Rhythm Rescue: Approach to SVT 2:00 - 2:10 Timing Matters: Surgical management of congenital heart disease 2:10 - 2:20风湿热复活2:20-3:10 pm来宾讲座2:20-2:45 pm心肌疾病:从心肌病到炎症2:45-3:10 pm卫生保健未来2.0 3:10-4:00