XiaoMi-AI文件搜索系统
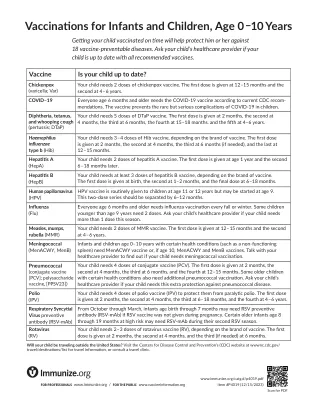
World File Search System婴儿和儿童的疫苗接种,年龄为0-10岁
您的孩子需要4剂共轭疫苗(PCV)。第一个剂量在2个月时给予,第二剂在4个月,第三剂在6个月,第四剂在12-15个月的第四剂。一些患有某些健康状况的大儿童也需要额外的肺炎球菌疫苗接种。询问您的孩子的医疗保健提供者是否需要对肺炎球菌病的额外保护。
亲爱的学龄学生的父母/监护人:
1剂量ACWY脑膜炎球菌共轭1剂量TDAP以下资源是获得所需疫苗接种的选择:•医师办公室:与您的医生办公室联系。•Macomb县卫生部门免疫诊所:与小时和约会的位置联系。首选任命。散步被接受为时间允许。有关更多信息,请访问:https://www.macombgov.org/departments/health-department/family-health-services/mmunization-clinic。
材料视野 - 英国皇家化学学会
脂肪族侧链影响固态填充并使聚合物可溶,这对于从溶液中加工聚合物至关重要,以及——可选—— (3) 额外的功能团,用于微调光学和电子特性,吸电子基团 (EWG) 或电子给体基团 (EDG),其电子给体特性比脂肪族侧链强。11-13 侧链和额外的功能团通常组合成连接到 p 共轭主链的相同取代基(图 1c)。这三个部分中的每一个都需要仔细选择,因为它们决定了聚合物的性质,最重要的是前线分子轨道(HOMO 和 LUMO)能级,从而决定带隙。带隙很重要,因为它决定了 OLED 应用中发射的光的波长,也决定了 OPV/OPD 应用中吸收的太阳光谱的比例。然而,除了带隙要求外,还需要仔细控制共轭聚合物的前线分子轨道能级,以便与电极的功函数进行适当的匹配,或促进组分材料之间所需的电荷分离或转移过程。14
氮化碳及其磁性特征中的光诱导的自由基
g-cn是一个非特异性的术语,它包括一个相当广泛的材料家族,由石墨层和/或富含N型芳族环的聚合物链组成。单体单元由1,3,5-三嗪[2]或三嗪(也称为己嗪)部分由SP 3杂交N原子连接起来。[3]氮的原子C/N比有很大的变化,例如,对于理想的石墨结构,其对应于0.75,而对于更现实的(和讨论)的三嗪单元结构,理论C/N原子比为0.67,而C/H ATOMIC比率为2.0。cn仅包含地球丰富的元素碳,氮和氢,可以从廉价且易于获得的前体合成,并且具有较高的化学和热稳定性,这是由于共轭层结构中成分之间的强相价键。由于广泛的共轭,CN在电磁频谱的可见区域吸收,带隙为2.7 eV(= 460 nm),并且已成功地用于催化广泛的反应。由于所有这些原因,G-CN迅速成为当前光催化研究的主要参与者。[4]
hello@acoerela.com - 铼生物
1. Zhou, C., Chia, GWN, Ho, JS, Moreland, AS, Seviour, T., Liedberg, B., Parikh, AN, Kjelleberg, S., Hinks, J., & Bazan, GC (2019). 链延长的寡苯乙烯电解质可提高微生物膜稳定性。Advanced Materials, 31(18)。https://doi.org/10.1002/adma.201808021 2. Zhou, C., Ho, JS, Chia, GWN, Moreland, AS, Ruan, L., Liedberg, B., Kjelleberg, S., Hinks, J., & Bazan, GC (2020)。使用共轭寡电解质进行革兰氏分型。Advanced Functional Materials, 30(42)。 https://doi.org/10.1002/adfm.202004068 3. Zhou, C.、Li, Z.、Zhu, Z.、Chia, GWN、Mikhailovsky, A.、Vázquez, RJ、Chan、SJW、Li, K.、Liu, B. 和 Bazan, GC (2022)。用于通过增量 NIR-II 发射进行长期肿瘤追踪的共轭寡电解质。先进材料,34(20).https://doi.org/10.1002/adma.202201989 4. Zhou, C.、Cox-Vázquez、SJ、Chia、GWN、Vázquez、RJ、Lai、HY、Chan、SJW、Limwongyut, J. 和 Bazan, GC (2023)。基于共轭寡电解质的水溶性细胞外囊泡探针。Science Advances,9(2)。https://doi.org/10.1126/sciadv.ade2996 5. Pham, TT、Le, AH、Dang, CP、Chong, SY、Vinh, D.、Peng, B.、Jayasinghe, MK、Ong, HB、Hoang, DP、Louise, RA、Loh, Y.、Hou, HW、Wang, J. 和 Le, MT (2023)。巨噬细胞对红细胞细胞外囊泡的内吞作用导致细胞质血红素释放并防止动脉粥样硬化中的泡沫细胞形成。Journal of Extracellular Vesicles,12(8)。https://doi.org/10.1002/jev2.12354
量子计算
1 向量和矩阵基础 3 1.1 向量空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.4.3 Gram-Schmidt 正交化 . . . . . . . 10 1.5 线性算子和矩阵 . . . . . . . . . . 11 1.5.1 Hermitian 共轭矩阵、Hermitian 矩阵和酉矩阵 . . . . . . . . . . . . 12 1.6 特征值问题 . . . . . . . . . . . . . 13 1.6.1 埃尔米特矩阵和正规矩阵的特征值问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 1.10 张量积(克罗内克积)。 。 。 。 。 。 。 。 。 。 。 。 。 。 26
论量子信道的混合酉秩
在量子信息理论中,对于任何维度为 n 的正整数,混合酉量子信道是那些可以用 n × n 复酉矩阵的共轭凸组合表示的线性映射。我们考虑任何此类信道的混合酉秩,它是这种形式表达所需的最少不同酉共轭个数。我们确定了混合酉信道的混合酉秩 N 和 Choi 秩 r 之间的几种新关系,Choi 秩等于该信道的 Kraus 表示所需的最少非零项个数。最值得注意的是,我们证明了对每个混合酉信道都有不等式 N ≤ r 2 − r + 1 满足(当 r = 2 时,等式 N = 2 也是如此),并且我们展示了已知的第一个满足 N > r 的混合酉信道的例子。具体来说,我们证明对于无穷多个正整数 d (包括每个素数幂 d ),存在 Choi 秩为 d + 1 和混合酉秩为 2 d 的混合酉信道。我们还研究了混合酉 Werner-Holevo 信道的混合酉秩。
使用镍(II)Allyl系统对丁二烯的协调链转移聚合:直接径丁二烯的直接途径
摘要:镍烯丙基复合物是丁二烯(BD)1,4-会员聚合物的催化剂。协调链转移聚合(CCTP)尚未使用这些系统评估。我们在这项工作中报告了丁二烯在存在π-甲基镍(II)三氟乙酸(TFA)和MG N BUET或ALET 3作为链转移剂(CTA)案例研究的情况下的聚合。反应遵循一阶动力学与单体相比。在CTA存在的情况下证明了链的转移,并形成带有共轭二烯部分的多丁二烯。这允许通过重新插入链条一锅访问分支多丁二烯。多丁二烯氢化后,通过13 c NMR定量分析分支,并评估了其对氢化样品的热性能的影响,特别是对于无法定量确定的低度分支。暂时提供了催化循环的完整描述。如果在乙烯聚合过程中在文献中描述了类似的串联过程,据我们所知,这是迄今为止报道的唯一用于共轭二烯的系统,导致分支多丁二烯,从而扩展了CCTP过程的应用范围。■简介
2024年11月20日至22日研究所查尔斯·萨德隆(Charles Sadron) - 斯特拉斯堡
Martin Brinkmann博士,ICS培训2:结构和形态对掺杂聚合物半导体共轭聚合物(CPS)的热电特性的影响在塑料电子中以半导体和导电聚合物的形式无处不在,这些聚合物是诸如诸如太阳能电池,现场效应型和热型晶体管和热型晶体和热型的诸如诸如太阳能电池中的集中的。利用这种共轭材料的各向异性特性要求采用先进有效的生长和方向方法。首先,此贡献回顾了塑料电子中使用的共轭聚合物的不同比对方法。第二,我们介绍了高温摩擦方法的艺术状态,该方法广泛用于制造排列的聚合物半导体(PSC)和导电聚合物(CP)膜。示例用于说明这种大规模取向的多功能方法如何用于设计具有各向异性光学特性的设备。Finally, we emphasize the recent progress made in the fabrication of highly ordered and oriented CPs by controlled doping of well-crystallized PSCs such as regioregular poly(3- hexylthiophene-2,5-diyl) and poly[2,5-bis(3-dodecylthiophen-2-yl)thieno[3,2- b ]thiophene].将掺杂分子引入并修改这些PSC的晶体晶格的方式。讨论了聚合物的半晶结构对定向薄膜的掺杂和产生的热电性能的影响。伊夫琳·马丁(Evelyne Martin)博士,ICUBE培训3:热瞬变的原子尺度建模:应用于纳米结构,无定形和聚合物材料。在本演示文稿中,我将使用从头算分子动力学(将召回的原理)模拟在原子量表上描述的材料中的热瞬变。i将显示如何用于提取导热率及其由于微型化而引起的变化。我将介绍不同材料,晶体,无定形和有机材料的情况,并讨论观察到的行为的基础。
量子计算:从线性代数到物理实现
1 向量和矩阵基础 3 1.1 向量空间 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.4.3 Gram-Schmidt 正交化 . . . . . . . 10 1.5 线性算子和矩阵 . . . . . . . . . . 11 1.5.1 Hermitian 共轭矩阵、Hermitian 矩阵和酉矩阵 . . . . . . . . . . . . 12 1.6 特征值问题 . . . . . . . . . . . . . 13 1.6.1 埃尔米特矩阵和正规矩阵的特征值问题 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23 1.10 张量积(克罗内克积)。 。 。 。 。 。 。 。 。 。 。 。 。 。 26