XiaoMi-AI文件搜索系统
World File Search System三聚氰胺 - 异氨酸Tris schiff碱是一种有效的碳钢抑制剂:体重减轻,电化学和表面研究
但是,许多有机腐蚀抑制剂对人类健康和环境有害。在酸性环境中,含有杂环和芳族杂环环的有机分子表现出更大的腐蚀抑制作用。5,13 - 18有机分子的吸附在化学和物理键合中。有机抑制剂的效果可以归因于它们的低电力和极高的极化性,从而使它们覆盖了巨大的金属表面并将电子迅速传递到空置原子轨道。19,三嗪环的化合物称为三聚氰胺具有三个氮原子,因此它是富含氮的分子。20,21这些氮原子很容易质子化,从而增加了三聚氰胺在极性溶剂中的溶解度。最近,在三聚氰胺衍生物为一系列目标(包括预防腐蚀)的应用中采取了实质性进展。三聚氰胺衍生物的显着抑制效率归因于
先进的 DFT-NEGF 传输技术,用于新型 2D-...
摘要 — 我们在此介绍我们在原子模型求解器 ATOMOS 中实现的先进 DFT-NEGF 技术,以探索新型材料和器件(特别是范德华异质结晶体管)中的传输。我们描述了使用平面波 DFT、随后进行 Wannierization 步骤和原子轨道 DFT 的线性组合的方法,分别导致正交和非正交 NEGF 模型。然后,我们详细描述了我们的非正交 NEGF 实现,包括非正交框架内的 Sancho-Rubio 和电子-声子散射。我们还介绍了从第一原理中提取电子-声子耦合并将其纳入传输模拟的方法。最后,我们将我们的方法应用于新型 2D 材料和器件的探索。这包括2D材料选择和动态掺杂FET,以实现最终的小型化MOSFET,vdW TFET的探索,特别是可以实现高导通电流水平的HfS 2 /WSe 2 TFET,以及通过金属半导体WTe 2 /WS 2 VDW结型晶体管的肖特基势垒高度和传输的研究。
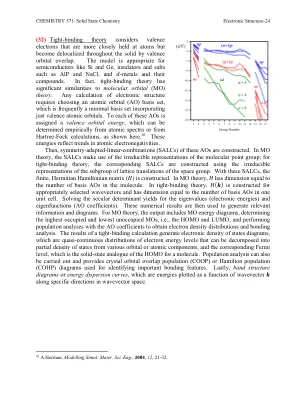
(32)紧密结合理论认为价电子更紧密地保持原子,但在整个固体中被视价轨道
(32)紧密结合理论认为价电子更紧密地保持原子,但在整个固体中被视价轨道重叠进行了离域。该模型适用于SI和GE等半导体,ALP和NACL等绝缘体和盐,以及𝑑金属及其化合物。实际上,紧密结合理论与分子轨道(MO)理论具有显着相似之处。电子结构的任何计算都需要选择原子轨道(AO)基集,该集通常是最小的基础集,仅包含价原子轨道。对这些AOS中的每一个都分配了价值轨道能,可以从原子光谱或Hartree-fock计算中进行经验确定,如下所示。10这些能量反映了原子电负性的趋势。然后,构建了这些AOS的对称适应性线性组合(SALC)。在MO理论中,salcs利用分子点群的不可约表示。对于紧密结合理论,使用空间群的晶格翻译亚组的不可约表示构建相应的salcs。 使用这些salcs,构建了有限的Hermitian Hamiltonian Matrix(𝐻)。 在MO理论中,𝐻具有等于分子中基本AO的数量。 在紧密结合理论中,为适当选择的波形构建,其尺寸等于一个单位细胞中的基础AOS数量。 求解特征值(电子能)和本征函数(AO系数)的世俗决定因素产率。在MO理论中,salcs利用分子点群的不可约表示。对于紧密结合理论,使用空间群的晶格翻译亚组的不可约表示构建相应的salcs。使用这些salcs,构建了有限的Hermitian Hamiltonian Matrix(𝐻)。在MO理论中,𝐻具有等于分子中基本AO的数量。在紧密结合理论中,为适当选择的波形构建,其尺寸等于一个单位细胞中的基础AOS数量。求解特征值(电子能)和本征函数(AO系数)的世俗决定因素产率。这些数值结果然后用于生成相关信息和图表。对于MO理论,输出包括MO能量图,确定最高占用和最低的无置置的MOS,即HOMO和LUMO,以及使用AO系数进行电子密度分布和键合分析的人群分析。紧密结合计算的结果产生了状态图的电子密度,这是电子能级的准连续分布,可以分解为来自各种轨道或原子成分的态密度,以及相应的FERMI水平,这是Homo的固态类似物的固态类似物。种群分析也可以进行,并提供用于识别重要键合特征的晶体轨道重叠种群(COOP)或汉密尔顿人群(COHP)图。最后,带结构图或能量分散曲线,这些曲线是沿波向量空间中特定方向的波形绘制的能量。
量子化学和光谱学
1. 微观物质的波粒二象性。经典力学无法描述原子和分子的结构。光和能量的量子。波粒二象性。德布罗意波及其实验观测。2. 薛定谔方程。微分方程。微观粒子的薛定谔方程。复数和复函数。概率和概率密度。波函数及其物理解释。算符、特征函数和特征值。汉密尔顿量。3. 自由和受限电子的平移运动。自由粒子。一维、二维和三维势箱中的粒子。盒中粒子模型的化学应用。化学键的矩形盒模型。穿过势垒的量子隧穿。4. 量子化学的数学形式。物理可观测量的算符。量子力学的假设。波函数的叠加。个体测量和期望值。交换和非交换算子。海森堡不确定性原理。跃迁偶极矩。光谱跃迁的强度。选择规则。5. 振动运动的量子力学描述。谐振子。谐振子的薛定谔方程。谐振子和双原子分子振动之间的联系。振动跃迁的选择规则。6. 旋转运动的量子力学描述。环中粒子的薛定谔方程。二维和三维旋转。角动量及其量化。球谐函数。双原子分子的刚性转子和旋转光谱。7. 氢原子的结构和光谱。单电子原子和离子的薛定谔方程。氢原子的能级、电子波函数和概率密度。原子轨道和量子数。自旋。8. 多电子原子。多电子波函数的轨道近似。自洽场。泡利不相容原理。构造原理和元素周期表。
化学粘合决定了两个看似相同的超导体的急剧临界温度差
尽管YB 6和实验室6具有相同的晶体结构,原子价电子的形象和声子模式,但它们表现出截然不同的声子介导的超导性。yb 6低于8.4 K的超导导,使其成为已知硼化物的第二个最高临界温度,仅次于MGB 2。实验室6直到接近 - 绝对零温度(低于0.45 K)才能超导。尽管以前的研究已经量化了Yb 6的更高费米 - 水平(E F)状态和较高的电子 - Phonon耦合(EPC)的规范超导性描述(EF),但尚未全面评估该差异的根源。通过化学键合,我们确定灯笼中的低谎言,未占用的4F原子轨道是这些超导体之间的关键区别。这些轨道在YB 6中无法访问,与πB– B键杂交,并使能量的能量低于σB-B键,否则在E f时。这种频段的反转至关重要:我们显示的光学声子模式负责超导性,导致Yb 6的σ-轨道在重叠中发生巨大变化,但彼此弱于实验室6的π轨道。yb 6中的这些声子甚至访问电子状态的交叉,表明EPC强。在实验室6中未观察到这种交叉。最后,显示了一个超级电池(m k-点)会发生PEIERL-喜欢YB 6中的效果,从柔软的声音子和相同的电子 - 耦合的光学模式中引入了其他EPC。总体而言,我们发现实验室6和YB 6具有从根本上不同的超导性机制,尽管它们差不多 - 身份差。
1年大学的课程要求...
生物医学工程学院的本科课程的详细概述1 - 学期I PHY 123:波浪和振荡,光学和热物理学3个学分,3个小时/周的波浪和振荡:简单的谐波振荡器,总能量,总能量,总能量,平均和谐型系统的差异方程两个身体振荡,质量减少,振荡,强迫振荡,共振;渐进波,固定波,组和相速度的波浪,功率和强度。光学:图像缺陷:球形像差,散光,昏迷,失真,曲率,色差。光理论;光线的干扰:Young的双缝实验,边缘的位移及其用途,菲涅尔双晶池,干扰薄膜的干扰,牛顿的环,干涉仪;光的衍射:菲涅尔和弗劳恩霍夫衍射,单缝衍射,圆形光圈的衍射,光学仪器的分辨能力,双裂和N裂缝的衍射,衍射,衍射光栅;极化:极化光的生产和分析,Brewster定律,MALUS定律,双重折射,Nicol Prism,光活性,偏光仪。Chem 125:有机和无机化学3个学分,3小时的原子结构:光,光和其他形式的电磁辐射的粒子和波质性质,原子光谱,原子光谱,BOHR模型,量子数,原子轨道;周期表:元素周期表,原子半径,电离能,电子亲和力,电负性。氧化和还原反应的基本概念。热物理学:温度测量原理:铂电温度计,热电温度计,高温计; Kinetic theory of gases, Maxwell's distribution of molecular speeds, Mean free path, Equipartition of energy, Brownian motion, van der Waal's equation of state, First Law of Thermodynamics and its application, Reversible and irreversible processes, Second Law of thermodynamics, Carnot cycle, Efficiency of heat engines, Carnot's theorem, Entropy and disorder, Thermodynamic functions, Maxwell relations, Clausius- Clapeyron方程,吉布斯相规,热力学第三定律。化学键合:不同类型的键合,共价键的细节,价键理论(VBT),分子几何形状,价壳电子对抑制(VSEPR)理论,轨道,分子轨道理论(MOT)的杂交。
用数值原子轨道的周期系统的Laplace实施MP2
二阶Møller-Plesset扰动理论(MP2)是一种后期的后期方法,用于考虑电子相关性效应。尽管形式非常简单,但它可以捕获约90%的相关能量(Bartlett和Stanton,2007年);因此,MP2方法仍然对量子化学感兴趣(Schütz等,1999; Kobayashi和Nakai,2006; Bartlett and Stanton,2007)和固态物理界(Suhai,1983,1983,1992; Sun and Bartlett; Sun and Bartlett,1996; Pisani et; Pisani et。但是,原始(典型)MP2方法的O(n 5)计算缩放限制了MP2方法在大系统中的应用。A series of algorithms have been proposed to speed up the calculations, such as local MP2 method ( Saebø and Pulay, 1993; Pisani et al., 2005, 2008; Maschio, 2011 ), Lapace-transformed MP2 method ( Häser and Almlöf, 1992; Häser, 1993; Ayala and Scuseria, 1999; Ayala et al., 2001;The local MP2 method proposed by Pulay ( 1983 ) and Saebø and Pulay ( 1993 ) has been efficiently implemented ( Schütz et al., 1999 ) in the MOLPRO code for molecules, then the periodic version of the local MP2 method has been implemented ( Pisani et al., 2005, 2008; Maschio, 2011 ) in the CRYSCOR code and in the CP2K code ( Usvyat等人,2018年)用于扩展系统。由于采用了空间局部的轨道或Wannier功能,因此局部MP2方法的计算缩放为O(n)。已经采用了局部原子轨道,计算缩放也为O(n)。最初由Häser和Almlöf(1992)和Häser(1993)提出了Laplace转化的MP2方法,并已针对分子(Ayala and Scuseria,1999)和扩展系统(Ayala等,2001,2001)实施了程序。拉普拉斯转换的MP2方法已与身份(RI)技术的分辨率相结合,以进一步改善