XiaoMi-AI文件搜索系统
World File Search System测量噪声
心血管系统的混合神经普通微分方程模型
在人类心血管系统（CVS）中，心脏的左侧和右心室之间的相互作用受隔膜和果皮的影响。CVS的计算模型可以捕获这种相互作用，但这通常涉及将解决方案近似于复杂的非线性方程。结果，已经提出了许多模型，其中这些非线性方程是简化的，或者忽略了心室相互作用。在这项工作中，我们提出了一种使用混合神经普通微分方程（ODE）结构来建模心室相互作用的替代方法。首先，模拟了CVS的总参数ode模型（包括牛顿 - 拉夫森程序作为数值求解器），以生成合成时间序列数据。接下来，构建了基于同一模型的混合神经极，而室性相互作用则由神经网络设置为政府。我们使用短范围的合成数据（带有不同量的测量噪声）来训练混合神经ode模型。符号回归用于将神经网络转换为分析表达式，从而导致部分学习的机械模型。这种方法能够以良好的预测能力恢复简约的功能，并且对测量噪声非常有力。
GPS 简介
3 GPS 误差和偏差 ...................27 3.1 GPS 星历表误差 .....................28 3.2 选择性可用性 ......................29 3.3 卫星和接收机时钟误差 ..............31 3.4 多路径误差。...................32 3.5 天线相位中心变化。..............34 3.6 接收机测量噪声。................35 3.7 电离层延迟 ....................36 3.8 对流层延迟 ..................38 3.9 卫星几何测量 .................39 3.10 GPS 任务规划 ..................42 3.11 用户等效范围误差 ..............44 参考文献 · · · · · · · · · · · · · · · · · · · · · · · 44
一种有效的带测量噪声的时变量子态在线估计算法
受在线交替方向乘法器方法 (OADM) 的启发，本文提出了一种高效的在线量子态估计 (QSE) 算法 (QSE-OADM) 用于恢复时变量子态。具体而言，在 QSE-OADM 中，密度矩阵恢复子问题和测量噪声最小化子问题被分开并分别求解，而无需迭代运行算法，这使得所提出的方法比所有先前的工作都更高效。在数值实验中，对于 4 量子比特系统，所提出的算法在 71 个样本后可以达到超过 97.57% (保真度) 的估计准确率，每次估计的平均运行时间为 (4.19±0.41)×10-4 秒，与现有的在线处理算法相比，其性能更为优越。
![arXiv:2006.13644v1 [quant-ph] 2020 年 6 月 24 日](/simg/g:\will\search\icon\source\0\07b3531d436e8a9fb02eec1e77f04882fa1c3acf.webp)
arXiv:2006.13644v1 [quant-ph] 2020 年 6 月 24 日
我们制定了一种算法，仅从部分信息（例如少体可观测量可获得的信息）来确定量子多体态之间保真度的下限。我们的方法特别适用于置换不变态，但在所有对称性仅为部分对称性的情况下，它都会给出非平凡的结果。此属性使其特别适用于原子集合实验，其中相关的多体态可通过集体测量来认证。例如，我们表明，仅通过测量 N = 100 个粒子的 ξ2 ≈− 6 dB 自旋压缩态，即可以高达 F = 0.999 的保真度认证其极化和压缩正交。此外，我们还展示了如何定量考虑状态中的测量噪声和部分对称性，这使得我们的方法在实际的实验情况下很有用。
NYC噪声代码和电池储能系统（BESS）
●由于关键的噪声代码考虑因素存在很大的不确定性，因此从EOR获得认证非常具有挑战性。首先，DEP尚未发布有关如何将噪声代码应用于BES的任何指导，如下面的第二节中所述。噪声顾问和EORS几乎没有确定合规性的基础。第二，建模的噪声水平并不总是反映运行数据；事先证明项目将符合噪声代码，需要开发复杂的声学建模，该建模考虑系统将如何与特定于网站的条件相互作用。构建系统后，这种建模将永远不会像测量噪声条件一样准确，引入了一种不确定性的水平，这使得很难先发出证明合规性。
STC31-C 设计指南
• 低交叉敏感性：（推荐的标准测量模式）在此测量模式下，湿度、温度、压力和氧气对 CO 2 测量的影响显著降低。因此，在大多数情况下建议使用低交叉敏感性模式。它提供高达 7Hz 的采样频率，对气体变化的物理响应时间与低噪声模式相同。• 低噪声：低噪声测量模式的优势在于采样率稍快（10Hz）且测量噪声较低，但对湿度、温度、压力和氧气表现出明显的交叉敏感性，因此不推荐用于大多数用例。此模式的通信接口与前代传感器 STC31（NRND Mai 2024）保持相同，以实现向后兼容。无论测量模式如何，都需要将压力、湿度（和温度）作为输入提供给 STC31-C，以实现指定的浓度测量精度。
主动感测以改进模型学习的数据质量
摘要 - 在机器人技术的机器学习中，培训数据质量具有至关重要的作用。许多方法都使用利用算法来选择模型最有用的数据点，通常会忽略测量噪声对数据的影响。本文介绍了一种增强模型学习数据集质量的方法，优化了探索和主动传感指标的组合。我们介绍了一种基于高斯工艺的新型探索格拉米亚度量，预测协方差矩阵，优化以探索有关未知模型的知识最大的状态空间区域。这些与主动传感度量（gramian）集成在一起，以减轻测量噪声效应。通过在独轮车和四倍的机器人上进行模拟来证明这种方法的有效性，证实了组合主动感应和探索可以显着提高模型学习中的性能。
Zachary R. Madin
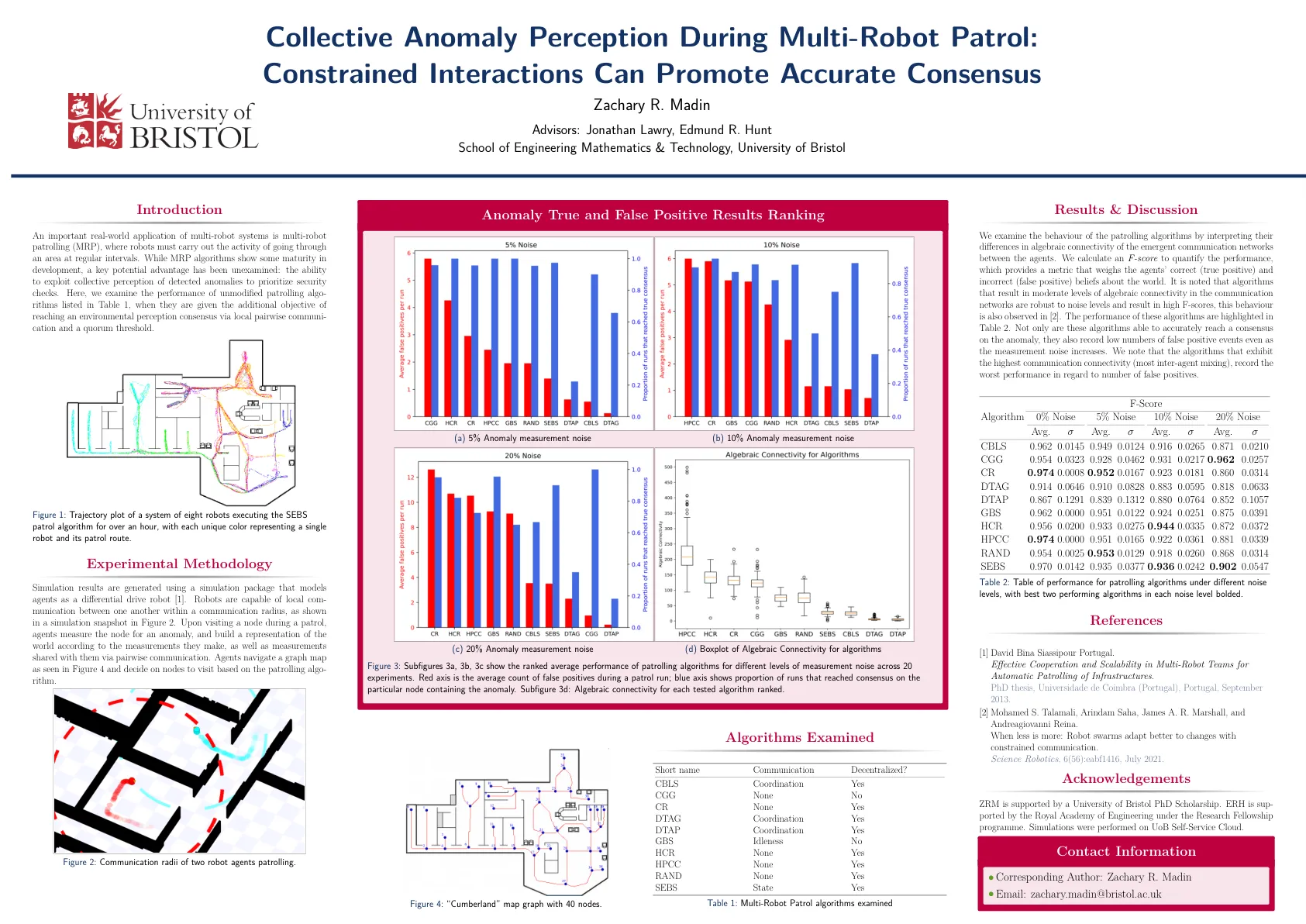
我们通过解释巡逻算法的行为来解释其在代理之间紧急通信网络的代数连通性中的差异。我们计算一个F得分来量化性能，该表现提供了一个权衡代理商正确（真正的积极）和不正确（误报）对世界的指标。注意到，通信网络中导致代数连接中等水平的算法对噪声水平有牢固的态度，并导致较高的F分数，在[2]中也观察到了此行为。这些算法的性能在表2中突出显示。这些算法不仅能够准确达成异常共识，而且还记录了较少的假阳性事件，即使测量噪声增加。我们注意到，表现出最高通信连接性的算法（最间隔的混合），记录了关于误报数量的最差性能。
pos（lattice2024）212-科学论文集
푍（2）晶格量规理论在研究量子代码的量子误差校正阈值概率（QEC）的研究中起着重要作用。对于某些QEC代码，例如众所周知的Kitaev的复曲面/表面代码，可以将QEC解码问题映射到给定噪声模型的统计力学模型上。对阈值概率的研究对应于映射统计力学模型的相图。这可以通过统计力学模型的蒙特卡洛模拟来研究。在[11]中，我们研究了在二维上与综合征测量噪声一起在旋转/表面代码上的逼真噪声模型的影响，并引入了随机耦合 - 平面仪表模型，三维푍（2）×푍（2）×푍（2）lattice Gauge理论。这个新的Z（2）量规理论模型捕获了在去极化和综合征噪声下的紫杉/表面代码的主要方面。在这些程序中，我们主要关注Mont Carlo模拟的各个方面，并讨论了Monte Carlo模拟Z（2）晶格理论的初步结果。