XiaoMi-AI文件搜索系统
World File Search System物理(物理)
物理1201q。一般物理I.(4个学分)一个基于非库的课程,介绍了应用于机械现象的力和运动定律。概念,例如工作,机械能,线性和角动量以及能量保护。 实验室提供了精确测量的基本培训。 Ca 3-LAB。 注册要求:数学1060Q或相当于数学放置评估预估算的资格分数(plopement.uconn.edu/mathematics-placement)。 不向已通过Phys 1401Q,1501Q或1601Q的学生开放。 通过Phys 1202Q后,可能不会从序列中取出。 技能代码:comp:量化能力内容领域:CA3LAB:科学与技术实验室询问主题:TOI6L:Science EMP INQ(实验室)查看类(https://catalog.uconn.edu/course-search/? 详细信息和代码= Phys%201201Q)概念,例如工作,机械能,线性和角动量以及能量保护。实验室提供了精确测量的基本培训。Ca 3-LAB。 注册要求:数学1060Q或相当于数学放置评估预估算的资格分数(plopement.uconn.edu/mathematics-placement)。 不向已通过Phys 1401Q,1501Q或1601Q的学生开放。 通过Phys 1202Q后,可能不会从序列中取出。 技能代码:comp:量化能力内容领域:CA3LAB:科学与技术实验室询问主题:TOI6L:Science EMP INQ(实验室)查看类(https://catalog.uconn.edu/course-search/? 详细信息和代码= Phys%201201Q)Ca 3-LAB。注册要求:数学1060Q或相当于数学放置评估预估算的资格分数(plopement.uconn.edu/mathematics-placement)。不向已通过Phys 1401Q,1501Q或1601Q的学生开放。可能不会从序列中取出。技能代码:comp:量化能力内容领域:CA3LAB:科学与技术实验室询问主题:TOI6L:Science EMP INQ(实验室)查看类(https://catalog.uconn.edu/course-search/?详细信息和代码= Phys%201201Q)
物理(物理)
物理5350。计算物理学简介。(3个学分)计算物理学简介,包括C,C ++和Python中的编程。主题包括普通微分方程,有限的差异和稳定性分析,在超过一个维度中的部分微分方程(例如Schroedinger和扩散方程)的数值解决方案,Krylov空间方法(例如,特征系统溶解器和Matrix Inversion)和Monte Carlo集成。可以涵盖介绍性机器学习和高性能计算方法。编写代码以解决物理和天体物理学选定领域的当前问题。注册要求:建议准备:Python,C,C ++,UNIX。查看类(https://catalog.uconn.edu/course-search/?详细信息和代码= Phys%205350)
sc tokai应用物理学会学术演讲(JSAP SCTS 2014)
简介:在过去的几十年中,碳纳米材料(例如碳纳米纤维(CNF)和石墨烯)由于其宏伟的特性而引起了强烈的科学兴趣[1,2]。关于石墨烯的大部分研究都是针对合成高质量和大面积石墨烯方法的探索。有希望的方法是脉搏激光沉积和化学蒸气沉积。虽然在理解石墨烯合成方面已经取得了重要成就,但它们的形成机制尚不清楚。现场技术的最新进展现在为研究原子水平研究固相相互作用的新可能性提供了新的可能性。在这里,我们报告了通过原位透射电子显微镜(TEM)直接观察到铜含有铜纳米纤维(CU-CNFS)的结构转化。实验:使用kaufmann型离子枪制造Cu-CNF(iontech。Inc. Ltd.,模型3-1500-100FC)。所使用的样品是尺寸为5x10x100 µm的市售石墨箔。通过在CNFS生长过程中连续供应Cu,在室温下用1 keV ar +离子辐射石墨箔的边缘。在其他地方详细描述了离子诱导的CNF生长机理的细节[3]。然后将Cu-CNF安装在200 kV的TEM(JEM2010,JEOL CO.,JEOL CO.)的阴极微探针上,并研究了Cu-CNFS向石墨烯的结构转化,在电流 - 电压(I-V)测量过程中进行了研究。结果和讨论:在I-V测量过程中,高温是通过Cu-CNF结构中的Joule加热获得的。焦耳CNF的加热导致其表面石墨化,最后在转化为严重扭曲的石墨烯中。tem图像表明,最初,CNF在本质上是无定形的,而I-V过程中的电流流动引起了CNF的晶体结构的急剧变化,形成了石墨烯的薄层(1-3层)。作为结果,在产生的电流大大增加的情况下,改进了结构的电性能,比初始值高1000倍(从10 -8到10 -5 a)。该过程采用三个步骤进行:Cu纳米颗粒的聚集,无定形碳扩散到Cu中,以及在进一步加热下的Cu纳米颗粒的电迁移。
XIV年轻科学家会议“理论物理问题” /科学计划< / div>
早上会议_________ 10-05塔拉斯·帕特萨汉(Taras Patsahan)讲座“无序多孔媒体中离子液体的阶段行为”,乌克兰NAS的凝结物理学研究所,lviv ____________ 10-50 oleg gerasymov,liudmyla sidletska“朝着公平的环境中的媒体迁移, Ukraine ___________ 11-10 Oleg Gerasymov, Heorhiy Kudashkin "Towards the influence of compaction on the compressibility of a model bi-component mixture” Odesa State Environmental University, Odessa, Ukraine __________ 11-30 Yulian Honchar, Bertrand Berche, Yurij Holovach, Ralph Kenna “How partition function zeros help find out the finite-size scaling上方的上面临界维度”乌克兰NAS的凝结物理学研究所,lviv ____________ 11-50休息______________ 12-10 Oleh Yermakov“光线内纤维耦合理论及其在增强光收集中的应用”
物理理论的自我测试,或者量子理论对于某些信息处理任务来说是否最佳?
自测试通常是指采取一组给定的观察到的相关性,这些相关性被认为是通过量子理论准确描述的过程产生的,并试图推断量子态和测量值。换句话说,它关心的是我们是否可以通过仅查看量子黑盒设备的输入输出行为来判断它们在做什么,并且已知在几种情况下是可能的。在这里,我们提出一个更普遍的问题:是否有可能对一个理论,特别是量子理论进行自测试?更准确地说,我们问在特定的因果结构中是否存在只能在任何情况下具有与量子力学相同相关性的理论中执行的任务。我们提出了这种相关性自测试的候选任务,并在一系列广义概率理论 (GPT) 中对其进行了分析,结果表明这些理论都没有比量子理论表现更好。我们的研究结果概括起来就是,对于这项任务来说,所有非量子 GPT 都严格劣于量子力学,这将为公理化量子理论提供一种新方法,并能够通过实验测试同时排除此类 GPT。
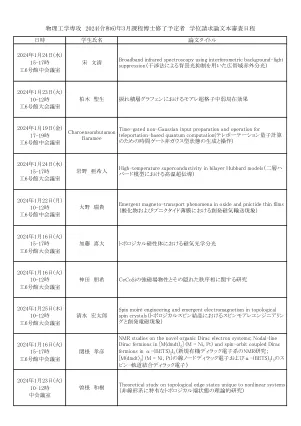
物理工学専攻 2024(令和6)年3月课程博士修了予定者 学位 ...
nmr对[M(DMDT)2](M = Ni,PT)中的Nodal-line Dirac Fermions进行 NMR研究; DMDT)2 I 3)NMR研究; DMDT)2 I 3)
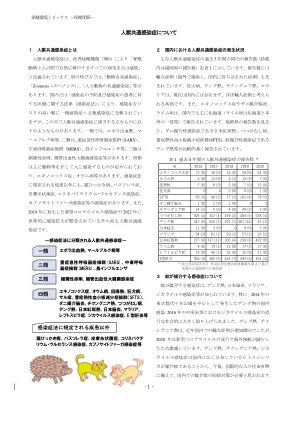
关于人畜共患疾病 - 福生县卫生与环境研究所
gengorobuna * carassius cuvieri○□○□□□□carassius sp○□●■做○□○□○□●■□丢失的鱼 *疑虑的anguillicaudatus○○○□cat鱼Rhinogobius sp○□○□●○□●○□○□□□■
Petz 恢复通道的量子算法和非常好的测量
1 加州理工学院量子信息与物质研究所,美国加利福尼亚州帕萨迪纳 91125 2 西蒙斯计算理论研究所,美国加利福尼亚州伯克利 94720 3 麻省理工学院机械工程系和电子研究实验室,美国马萨诸塞州剑桥 02139 4 杜克大学物理系和电气与计算机工程系,美国北卡罗来纳州达勒姆 27708 5 斯坦福大学信息系统实验室,美国加利福尼亚州斯坦福 94305 6 路易斯安那州立大学赫恩理论物理研究所、物理与天文系和计算与技术中心,美国路易斯安那州巴吞鲁日 70803 7 斯坦福大学斯坦福理论物理研究所,美国加利福尼亚州斯坦福 94305