XiaoMi-AI文件搜索系统
World File Search System相关曲线
局部场电位以特异性和频率依赖性方式反映了皮质种群动力学
皮质神经元种群的尖峰活性通过少数人口范围的协方差模式（“潜在动力学”）很好地描述。这些潜在动力学在很大程度上是由确定局部场电位（LFP）产生的相同相关的突触电流驱动的。然而，潜在动力学和LFP之间的关系仍然在很大程度上尚未探索。在这里，我们为灵长类动物感觉运动皮层的三个不同区域表征了这种关系。潜在动力学和LFP之间的相关性是频率依赖性的，并且在各个区域之间有所不同。但是，对于任何给定的区域，这种关系在各个行为之间保持稳定：在主电动机和前皮层中，LFP-LANTENT动力学相关曲线在运动计划和执行之间非常相似。LFP与神经群体潜在动力学之间的这些强大关联有助于弥合使用两种记录的行为神经相关性的研究丰富的研究。
脑电图中与性别相关的模式及其在机器学习分类器中的相关性
图1用迷你尖端卷积神经网络和相关归因方法进行性检测。首先，xðÞ节X段是交叉相关的吗？ðÞ，有16个学识渊博的时空内核（K I）的维度与脑电图的短窗口相似（图2中描述的实际核）。由于内核具有与数据相同数量的通道，因此它们仅沿时间轴而不是跨通道滑动。16个相关曲线被整流（Relu激活），并分为40个重叠的窗口。接下来，平均将窗户的最大值（M ij）进行。在最后一层中，从这16个平均值中预测了性别yðÞ。事后，网络参数用于归因于每个eeg通道和录音中的时间点的相关性r（紫色中指示的路径）。最终分类器层的重量（W I）的符号表示与第一层（ /emale /Red and + / + /男性 /蓝色）的每个内核相对应的性别。
利用纠缠光子违反 CHSH 不等式
2022 年诺贝尔物理学奖授予了阿斯派克特 (Aspect)、克劳泽 (Clauser) 和蔡林格 (Zeilinger)，以表彰他们“对纠缠光子的实验，证明了贝尔不等式的违反并开创了量子信息科学” [1]。在本文中，我们描述了我们自己使用纠缠光子违反 CHSH 不等式（一种贝尔不等式）的实验。我们使用 qutools quED 纠缠演示器仪器通过自发参量下转换产生纠缠偏振光子。我们测量了旋转基底中的光子偏振，并计算出纠缠光子的 CHSH 相关值 | S | = 2.123±0.030>2 和非纠缠光子的 | S | <2。我们还生成了非经典相关曲线，描述了纠缠和非纠缠光子在连续偏振器角度范围内的偏振测量巧合。我们的结果证明了纠缠的非局域性，并阐明了对光子对极化测量的非经典相关性的更好的理解。
从定量磁共振>
半导体单壁碳纳米管（S-SWCNT）是一类重要的P-偶联有机半导体（OSC），可以启用新兴的光电应用。了解S-SWCNT中的电荷传输机制（通常是OSC）对于材料和设备设计至关重要。诸如光电，传感器，发光二极管，现场效应晶体管和热电设备等应用都需要良好的电导率和载体迁移率。测量OSC中电导率的常见方法不允许独立测量托管载体密度或移动性，因此很难回答重要的基本和应用问题并阻碍性能优化。为了解决这一知识差距，我们使用光吸收和核磁共振光谱开发了一种组合方法，以直接测量掺杂的S-SWCNT中的托管载体密度。我们证明了载体密度会影响电荷离域化，从而导致载体密度依赖性迁移率，这与被电离杂质散射限制的迁移率相反。将模拟与我们的实验数据结合起来会产生相关曲线，该曲线可以通过快速且随时可用的吸收光谱测量来确定掺杂的S-SWCNT中的载体密度。结果为OSC社区提供了一个有价值的路线图，用于调整，量化和优化载流子密度，以供广泛的能源收集和光电应用。
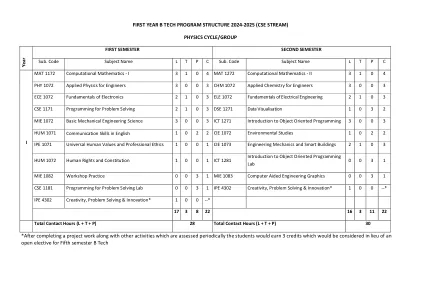
第一年 B TECH 课程结构 2024- ...
用数值方法求解方程。• CO5：应用插值概念求解数值微分和积分问题。教学大纲：矩阵代数：基本列变换和行变换、通过基本行运算求逆矩阵、矩阵的梯形和秩、线性方程组：一致性、高斯消元法、高斯-乔丹法、雅可比法和高斯-赛德尔法求解、特征值和特征向量：基本性质、谱矩阵分解、对角化、矩阵的幂。向量空间：向量概念向高维的推广、广义向量运算、向量空间和子空间、线性独立性和跨度、基。内积空间和 Gram-Schmidt 正交化过程。线性变换。微分方程及应用：一阶和高阶线性微分方程。用逆微分算子、参数变分法和待定系数法求解齐次和非齐次线性方程。代数和超越方程的解：参数曲线的追踪：摆线和相关曲线。二分法、试位法、牛顿-拉夫森法。用牛顿-拉夫森法求解非线性方程组。插值：有限差分和除差分。牛顿-格雷戈里和拉格朗日插值公式。牛顿除差插值公式。离散数值微分、数值积分：梯形法则、辛普森 1/3 法则和辛普森 3/8 法则。常微分方程的数值解：泰勒级数法、修正欧拉法、龙格-库塔法。参考书：