XiaoMi-AI文件搜索系统
World File Search System梅德斯通 - 博顿蒙奇尔西 - 帕森纳奇 2020 年 2 月.ai
出于任何目的依赖该信息的人必须通过检查或其他方式确保每条声明的正确性。这些细节是善意提供的,但不构成合同的一部分。任何声明都不应被视为事实陈述,有意向的各方 Core Commercial Limited, Unit 11 Offices, Dana Estate Transfesa Road, Paddock Wood, Kent TN12 6UT
舍伍德西概念规划
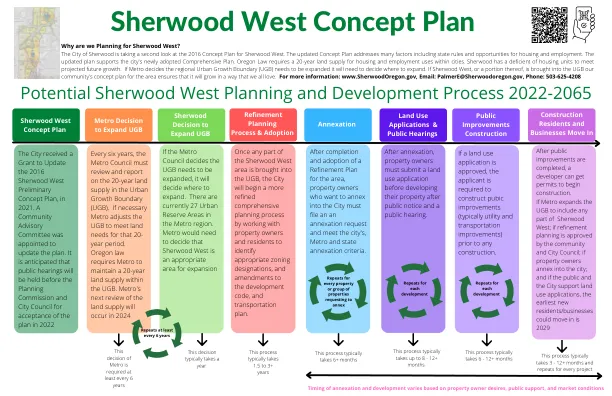
我们为什么要规划 Sherwood West?Sherwood 市正在重新审视 2016 年 Sherwood West 概念规划。更新后的概念规划解决了许多因素,包括州法规以及住房和就业机会。更新后的规划支持该市新通过的综合规划。俄勒冈州法律要求在城市内为住房和就业用途提供 20 年的土地供应。Sherwood 的住房单元不足以满足预计的未来增长。如果大都会决定需要扩大区域城市增长边界 (UGB),则需要决定在哪里扩展。如果 Sherwood West 或其中的一部分被纳入 UGB,我们社区对该地区的概念规划将确保它以我们都喜欢的方式发展。更多信息:www.SherwoodOregon.gov,电子邮件:PalmerE@Sherwoodoregon.gov,电话:503-625-4208
西迪布济德案例研究
昆虫种群在农业生态系统中发挥着至关重要的作用,影响着作物的生产力和整个生态系统的健康。这项研究在突尼斯西迪布济德省的 El-Mzara 1、El-Mzara 2 和 Zaafriya 三个地点进行,旨在通过水陷阱评估与番茄作物相关的昆虫的多样性和丰富度,时间为 2021 年 3 月下旬至 6 月初。捕获的昆虫被收集起来,并采用 RBA 方法进行鉴定。共捕获了 603 只昆虫。这种生物多样性属于九个目,共包含 108 个形态物种,分布在 46 个科中。结果显示,鞘翅目和膜翅目是最丰富的目,而膜翅目表现出最高的多样性,有 34 个形态物种。香农指数和辛普森指数表明 Mzara 1 的昆虫物种多样性高,分布均匀。Margalef 指数表明该地点的物种丰富度相对较高。昆虫生物多样性的时间分析表明,在整个番茄种植季节,不同目的昆虫的丰度存在差异。膜翅目昆虫在开花期达到顶峰,这与它们作为传粉媒介的作用相吻合。半翅目昆虫在结果和生长阶段最为丰富,这与它们对番茄叶片和果实的有害影响相对应。鳞翅目昆虫在结果和生长阶段也显示出丰度增加。这些首次发现有助于我们了解番茄作物中的昆虫群落结构。通过识别和监测主要昆虫种类及其辅助昆虫,所获得的数据为进一步研究提供了宝贵的基础。
德西特时空来自全息平面......
全息原理认为,体空间的自由度 (DoF) 被编码为边界量子场系统的信息 [1, 2, 3]。该原理的已知例子有黑洞熵 [4, 5, 6, 7] 和 d + 2 维反德西特时空/d + 1 维共形场论 (AdS d +2 /CFT d +1 ) 对应关系 [8, 9, 10, 11]。在发现 AdS d +2 /CFT d +1 对应关系中的全息纠缠熵的 Ryu–Takayanagi 公式 [12, 13, 14, 15] 后,多尺度纠缠重正化假设 (MERA) [16, 17] 被提出作为该公式背后的体量子纠缠的全息张量网络 (HTN),其中 d = 1 为零温度 [18, 19]。这里,MERA 是通过解纠缠器层(对我们而言是二分量子比特门)和粗粒化器层(等距)的半无限交替组合对量子比特中边界 CFT 2 的量子基态进行实空间重正化群变换 [16, 17]。MERA 是一个尺度不变的张量网络。基于对 HTN 的初步研究 [18, 20, 21],本文作者对 HTN 进行了经典化 [22, 23, 24, 25]。其中,HTN 的经典化是指在 HTN 中采用单量子比特的第三 Pauli 矩阵作为超选择规则算子 [25]。即,作用于 HTN 的希尔伯特空间的量子力学可观测量需要与第三 Pauli 矩阵交换,并根据这种交换性进行选择。HTN 经典化后,经典化全息张量网络 (cHTN) 的量子态对于所选可观测量在第三 Pauli 矩阵的特征基上没有量子干涉,因此等价于经典混合态,即第三 Pauli 矩阵乘积特征态的统计混合,
量子德西特宇宙有多圆?
摘要 我们研究了量子里奇曲率,它是在早期工作中引入的,在完整的四维量子引力中,以因果动力学三角剖分 (CDT) 的形式非微扰地表述。CDT 方法的一个关键发现是德西特型宇宙的出现,证据是蒙特卡罗对全局尺度因子量子动力学的测量与半经典迷你超空间模型的成功匹配。一个重要的问题是量子宇宙是否也在其更局部的几何性质方面表现出半经典性。利用新的量子曲率可观测量,我们检查量子几何的 (准) 局部性质是否类似于恒定弯曲空间的性质。我们发现证据表明,在足够大的尺度上,曲率行为与四维球面的曲率行为兼容,从而加强了用德西特空间来解释动态生成的量子宇宙。
塞缪尔·哈蒙德(Samuel Hammond)的书面证词-SST 2-5-25
16另请参见:Leif Rasmussen,“科学资金中的政治化和同质性的增加:NSF赠款的分析,1990 - 2020年”,《党派研究与意识形态研究中心》,2021年11月16日。 https://www.cspicenter.com/p/increasing-politicization-and-homogenity-in-scientific-funding-nsfunding-nsf-grants-nsf-grants-1 990-2020。
伊万·蒙日·康塞普西翁 (EIT)
Monge-Concepcion, I. 、Siroka, S.、Berdanier, R.、Barringer, M.、Thole, K. 和 Robak, C.,“非稳定涡轮边缘密封和叶片后缘流动效应”,ASME Turbo Expo 2021 论文集:涡轮机械技术会议和博览会,美国宾夕法尼亚州匹兹堡,GT2021-59273,2021 年。(已接受)。 Siroka, S.、Monge-Concepcion, I.、Berdanier, R.、Barringer, M.、Thole, K.、Robak, C.,“在叶片后缘流存在下将腔体密封效果与时间分辨的边缘密封事件关联起来”,ASME Turbo Expo 2021 论文集:涡轮机械技术会议和博览会,美国宾夕法尼亚州匹兹堡,GT2021-59285,2021 年。(已接受)。Monge-Concepcion, I.、Berdanier, R.、Barringer, M.、Thole, K.、Robak, C.,“评估叶片后缘流对涡轮边缘密封的影响”,ASME。涡轮机械杂志。2020;142(8):081001-081001-12。 doi:10.1115/1.4047611 Berdanier, R.、Monge-Concepcion, I.、Knisely, B.、Barringer, M.、Thole, K. 和 Robak, C.,“不同叶片跨度下定子-转子腔内的密封效果缩放”,ASME。《涡轮机械杂志》。2019 年;141(5): 051007-051007-10。doi:10.115/1.4042423
陆军军需品服务中央局
- CUESTA 皮埃尔-爱德华 ; - 戴斯勒 汤姆; - 达朗古尔·马蒂厄; - DARTENCET Sixte-Arnaud; - 德金妮·阿利克斯; - 德拉加德·劳伦; - 德梅高中; - 丹尼斯·雨果; - 德肖特·戈德弗罗伊: - 德肖蒙·朱迪思; - 亲爱的艾米琳; - 杜伊洛·克莱门斯; - PONTAVICE 路易斯; - 杜雅丁·维尼; - 埃利萨尔德·亚历山大; - 埃斯纳德·皮埃尔; - 莎拉·福佩尔; - 费利克斯·罗吉尔·米凯拉; - 弗朗克维尔·于格斯; - 加西亚·吉恩; - 德·吉弗里·艾蒂安; -格利帕·维克多; - 古尔梅伦·马蒂厄; - 吉勒敏在克洛希尔; - 游戏艾瑞尔; - 乔尔迪埃·伊索雷; - 不要阿尔法; - KERGOAT-PERRINET Océane ; - LA GORCE Thibault; - LABORDA Téva; - 拉布里特贾斯汀; - LABRUNE 利奥波德; - 英语恩佐; - 拉皮·罗曼; - LE BLEVENNEC Anaëlle; - 加洛本尼迪克特; - 十五个维克多; - 勒库克·塞泽尔; - 莱夫勒凡妮莎; - 苏菲传奇; - 莱昂·艾尔莎; - 路易斯·莱斯尤; -洛尔劳伦; - 光贾丝汀; - 马尔杰特·霍滕斯; - MARCILLET 西莉亚; - 马克·盖尔; - 马丁·威廉; - MONNERON 文森特; - 蒙伦·路易斯; - 蒙托亚·罗曼;