XiaoMi-AI文件搜索系统
World File Search SystemKansai医科大学概述2024Kansai医科大学概述2024
成立于1928年,Kansai医科大学(KMU)的历史悠久,并庆祝今年成立96周年。kmu基于其Jijinshinkyo的创始精神,即“仁慈,同情和同情心”,培养了具有丰富人性意识的优秀医生。随着与医疗保健相关的条件的迅速变化,社会越来越期望大学对大学的期望更多。kmu正在回应社会作为一所综合医科大学的期望,包括三个学院:医学学院和广阔的吉拉卡塔校园的护理学院,该校园充满了绿色植物,位于Yodogawa和Amanogawa Rivers,Amanogawa Rivers,以及Makino Campus of Hirtplace of Hirteplace kmu的Hablialitation。最近在KMU举行的活动是2022年2月的KMU塔的完成。塔楼是全球参与中心,KMU的全球化基地,国际学生的住房和医院酒店。这座塔楼是广场市中心最高的建筑结构之一,是KMU的象征和城市地标的象征。此外,2022年4月开设了近红外照片免疫疗法研究所的KMU。这是日本唯一的摄影疗法研究所,它具有第五次主要的癌症疗法。我们希望这将进一步推进KMU的教育,研究和医疗服务。KMU医院是一家指定的高级治疗医院,保持创新并且能力很高。其他后设施的设施是KMU医疗中心,第一家KMU分支机构,设有医院花园,
lai_cv.pdf - lucy lai 赖璐西
邀请会谈新加坡国立大学认知科学,心理学和AI研讨会系列系列2025年2月2025年赖斯大学,欧米茄PSI荣誉学会,2024年10月5日,《神经科学数学国际公约和AI国际公约》 2024年5月,5月5日1223年6月2023年6月2023年6月2022年2022年11月222日在增强地图上学习的RLDM研讨会,2022年6月2022年6月,斯坦福大学,心理学系,2022年5月,弗里塞姆弗里斯姆,哈佛大学,认知,大脑,大脑和行为SEMINAR,脑和行为SEMINAR,2022年2022年2月202日,麦克格尔大学,玛丽·麦克格尔大学。 Shenhav实验室2021年10月
动态卡西米尔效应的视角
今年,我们庆祝 Gerald T. Moore [1] 发表开创性论文 50 周年。这项工作让我们首次了解到一个令人费解的量子场现象——它预测当我们改变空电磁腔的边界条件(例如移动其中一个镜子)时会发生什么。从经典角度来看,什么都不应该发生——从某种意义上说,我们作用于一个不存在的物体。在量子物理学中,有一个时间-能量不确定性关系 ∆E∆t ≥ ℏ /2,这表明如果我们考虑小的时间间隔 ∆t,我们还需要考虑至少 ∆E ≥ ℏ /2∆t 的能量不确定性。因此,即使真空的能量为零,我们也需要考虑能量为 ∆E/2 的粒子及其反粒子自发出现,然后在时间 ∆t 内再次相互湮灭的可能性。我们无法从真空中提取这种所谓的零点能量,那么我们如何验证这种非常不平凡的虚无描述呢?1970 年,摩尔告诉我们,如果我们以足够快的速度移动镜子,我们就可以阻止湮灭,粒子就会被迫存在。这个过程被称为动态卡西米尔效应 (DCE)。能量来自镜子的运动,粒子通常成对产生。这种效应可以通过实验观察到吗?
排斥卡西米尔力和范德华力
材料表面之间电磁场的约束会导致后者之间产生力,这是由于前者的量子涨落造成的,这种力有许多有趣的特点。首先,这种力代表了真空量子性质的宏观表现,可以用当前的实验技术测量。其次,对自然界中的几种现象进行仔细研究后,有强有力的证据表明,粘附、摩擦、润湿和粘滞从根本上说是这些量子涨落的结果。第三,随着设备不断向纳米级小型化,设计物体间真空涨落的能力可能为改进设备架构、组装方法或功能铺平道路。在本文中,我们将简要讨论最近对长距离和短距离排斥力的测量、未来实验的测量方案,以及利用修改真空涨落约束产生的这些力的能力的技术机会。
Cirrus Aircraft Limited 西锐飞机有限公司
香港交易及结算所有限公司、香港联合交易所有限公司及香港中央结算有限公司对本文件的内容概不负责,亦不对其准确性或完整性作出任何陈述,并明确表示,对于因本文件全部或部分内容而产生或因依赖该等内容而引致的任何损失,概不负责。本文件的副本连同“附录五 — 交付公司注册处处长并可供展示的文件”所列文件,已根据《公司(清盘及杂项条文)条例》(香港法例第 32 章)第 342C 条的规定,由香港公司注册处处长登记。证券及期货事务监察委员会及香港公司注册处处长对本文件或上述任何其他文件的内容概不负责。
Cirrus Aircraft Limited 西锐飞机有限公司
香港交易及结算所有限公司、香港联合交易所有限公司及香港中央结算有限公司对本文件的内容概不负责,对其准确性或完整性不作任何陈述,并明确表示,对于因本文件全部或部分内容而产生或因依赖该等内容而引致的任何损失,概不负责。本文件的副本连同“附录五 — 交付公司注册处处长并可供展示的文件”所载文件,已根据《公司(清盘及杂项条文)条例》(香港法例第 32 章)第 342C 条的规定,由香港公司注册处处长登记。证券及期货事务监察委员会及香港公司注册处处长对本文件或上述任何其他文件的内容概不负责。
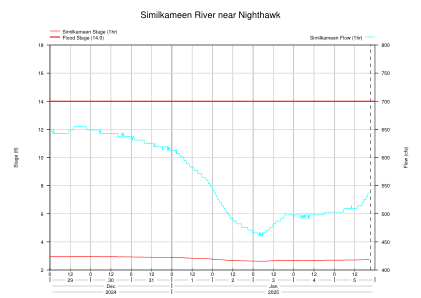
夜鹰附近的西米尔卡米恩河
2024 2025 十二月 一月 29 30 31 1 2 3 4 5 0 12 0 12 0 12 0 12 0 12 0 12 0 12 0 12 0 12