机构名称：
¥ 1.0
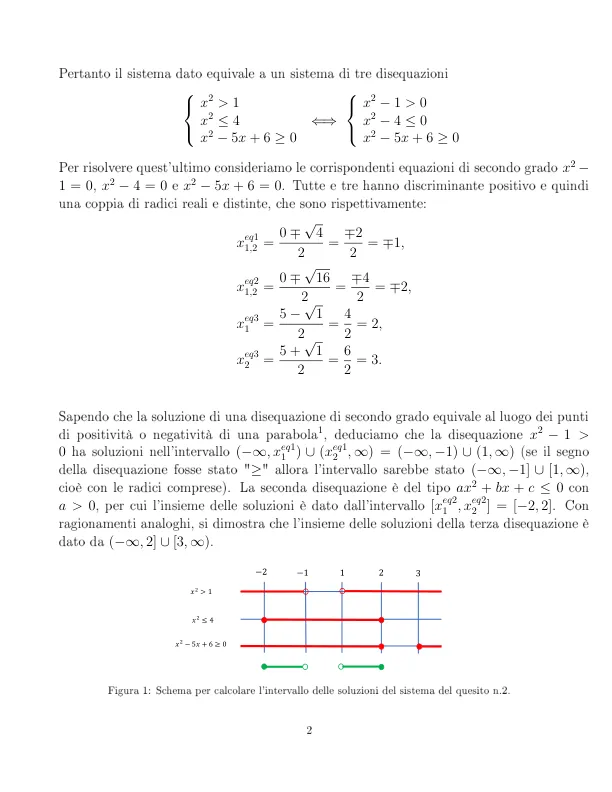
已知二次不等式的解等价于抛物线 1 的正点或负点的轨迹，我们推断不等式 x 2 − 1 > 0 在区间 ( −∞ , x eq 1 1 ) ∪ ( x eq 1 2 , ∞ ) = ( −∞ , − 1) ∪ (1 , ∞ ) 内有解（如果不等式的符号为 " ≥ "，则区间为 ( −∞ , − 1] ∪ [1 , ∞ ) ，即包含根）。第二个不等式属于 ax 2 + bx + c ≤ 0 类型，其中 a > 0 ，因此解集由区间 [ x eq 2 1 , x eq 2 2 ] = [ − 2 , 2] 给出。类似推理，可知第三个不等式的解集由 ( −∞ , 2] ∪ [3 , ∞ ) 给出。
不等式问题 1 的解答 - unipr
主要关键词
相关文件推荐
