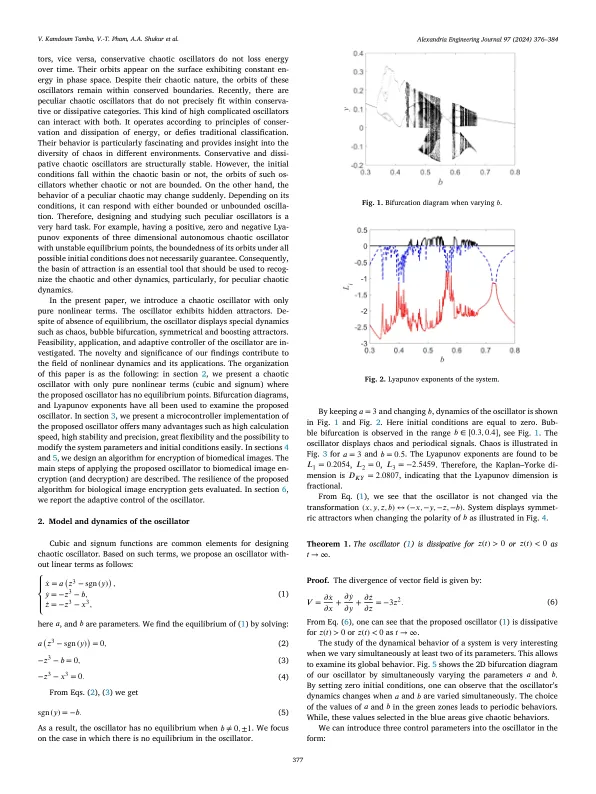
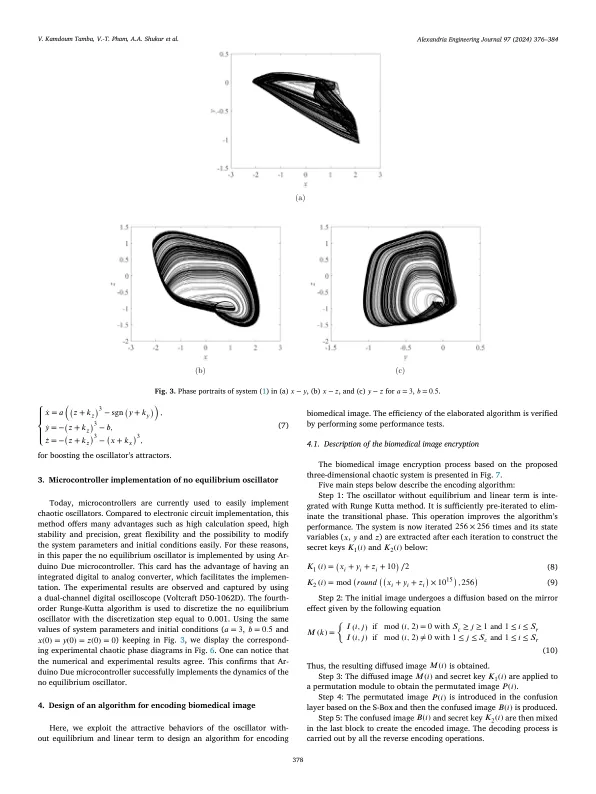
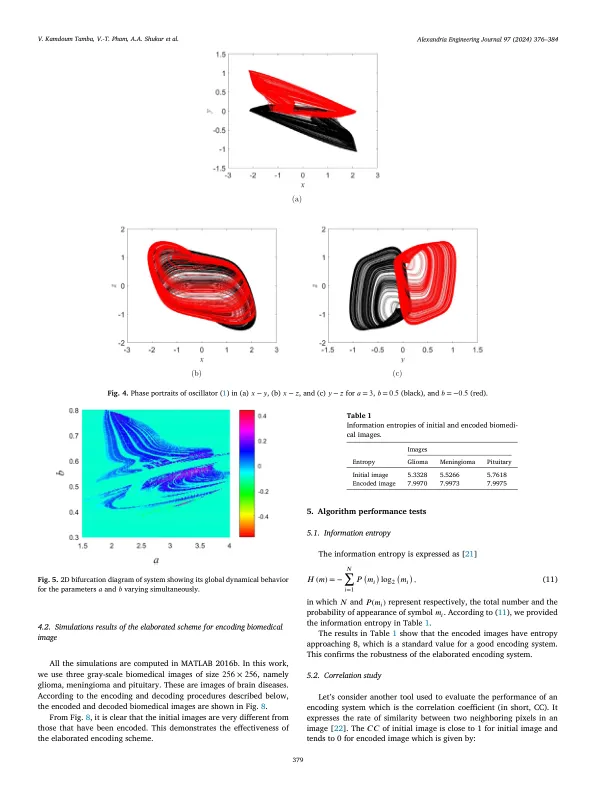
tors, vice versa, conservative chaotic oscillators do not loss energy over time. Their orbits appear on the surface exhibiting constant en- ergy in phase space. Despite their chaotic nature, the orbits of these oscillators remain within conserved boundaries. Recently, there are peculiar chaotic oscillators that do not precisely fit within conserva- tive or dissipative categories. This kind of high complicated oscillators can interact with both. It operates according to principles of conser- vation and dissipation of energy, or defies traditional classification. Their behavior is particularly fascinating and provides insight into the diversity of chaos in different environments. Conservative and dissi- pative chaotic oscillators are structurally stable. However, the initial conditions fall within the chaotic basin or not, the orbits of such os- cillators whether chaotic or not are bounded. On the other hand, the behavior of a peculiar chaotic may change suddenly. Depending on its conditions, it can respond with either bounded or unbounded oscilla- tion. Therefore, designing and studying such peculiar oscillators is a very hard task. For example, having a positive, zero and negative Lya- punov exponents of three dimensional autonomous chaotic oscillator with unstable equilibrium points, the boundedness of its orbits under all possible initial conditions does not necessarily guarantee. Consequently, the basin of attraction is an essential tool that should be used to recog- nize the chaotic and other dynamics, particularly, for peculiar chaotic dynamics.
Oscillator without equilibrium and linear terms - IRIS