XiaoMi-AI文件搜索系统
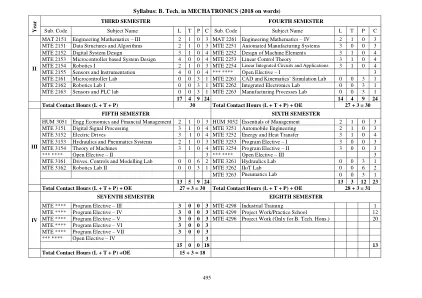
World File Search System教学大纲:机电一体化技术学士学位(2018 字)
向量微积分:梯度、散度和旋度,它们的物理意义和恒等式。线、表面和体积积分。格林定理、散度陈述和斯托克斯定理、应用。傅里叶级数:周期函数的傅里叶级数、欧拉公式。奇函数、偶函数和任意周期函数的傅里叶级数。半程展开。傅里叶积分。正弦和余弦积分、傅里叶变换、正弦和余弦变换。谐波分析。偏微分方程:基本概念、仅涉及一个变量的导数的方程解。通过指示变换和变量分离求解。用分离变量法推导一维波动方程(振动弦)并求其解。达朗贝尔波动方程解。用高斯散度定理推导一维热方程并求一维热方程解。用分离变量法求解。数值方法:一阶和二阶导数(常导数和偏导数)的有限差分表达式。边界值问题的解,二阶偏微分方程的分类。用标准五点公式求拉普拉斯和泊松方程的数值解,用显式方法求热和波动方程的数值解。参考文献: 1.Kreyszig, Erwin,《高级工程数学》,John Wiley & Sons,(第 5 版),2010 年。2.3.S. S. Sastry,《数值分析入门方法》(第 2 版),1990 年,Prentice Hall。B. S. Grewal,《高等工程数学》,1989 年,Khanna Publishers 4。Murray R. Spiegel,《矢量分析》,1959 年,Schaum Publishing Co.
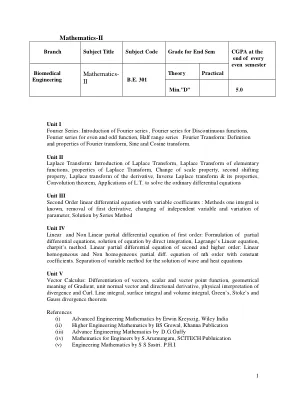
数学-II - 分支学科名称学科代码年级...
第一单元 傅里叶级数:傅里叶级数简介、不连续函数的傅里叶级数、偶函数和奇函数的傅里叶级数、半程级数 傅里叶变换:傅里叶变换的定义和性质、正弦和余弦变换。 第二单元 拉普拉斯变换:拉普拉斯变换简介、初等函数的拉普拉斯变换、拉普拉斯变换的性质、尺度变化性质、二阶平移性质、导数的拉普拉斯变换、逆拉普拉斯变换及其性质、卷积定理、应用 LT 解常微分方程 第三单元 变系数二阶线性微分方程:方法 已知一个积分、去除一阶导数、改变独立变量和改变参数、用级数法求解 第四单元 一阶线性和非线性偏微分方程:偏微分方程的公式、直接积分解方程、拉格朗日线性方程、查皮特方法。 二阶及高阶线性偏微分方程:具有常系数的 n 阶线性齐次和非齐次偏微分方程。分离变量法解波动和热方程 第五单元 向量微积分:向量的微分、标量和向量点函数、梯度的几何意义、单位法向量和方向导数、散度和旋度的物理解释。线积分、面积积分和体积积分、格林散度定理、斯托克斯散度定理和高斯散度定理 参考文献
2024-2025 年学习课程
APL101 工程应用中的应用数学 3 学分 (3-0-0) 常微分方程:二阶 ODE、待定系数法、参数变异、Strum-Liouville 特征值问题、差分方程。偏微分方程:PDE 的分类、热、波和拉普拉斯方程、分离变量以解决 PDE。傅里叶变换:傅里叶正弦变换、傅里叶余弦变换、解决 ODE 和 PDE 的技术。概率论:概率公理、条件概率、随机变量、工程系统中的不确定性、离散和连续分布、分布函数、联合概率分布、矩、协方差、相关系数。随机过程:随机过程的定义、随机 FE 模型、平稳过程、马尔可夫链、泊松过程。
Microsoft PowerPoint - 2020 年超材料大会网页版
“在局部傅里叶变换的维格纳表示中……可以有正值和负值,这会导致整个函数的傅里叶积分出现细微的抵消”
科学人工智能的“黑匣子”无法与 200 年历史的方法相提并论
训练尖端的深度神经网络需要大量数据,而使用当前方法进行重新训练的负担仍然很大。在对深度学习网络进行训练和重新训练以执行涉及复杂物理的不同任务后,莱斯大学的研究人员使用傅里叶分析比较了两次迭代中的所有 40,000 个内核,发现超过 99% 是相似的。此图显示了重新训练前(左)和重新训练后(右)差异最大的四个内核的傅里叶光谱。研究结果表明,该方法有可能找到更有效的重新训练路径,并且需要的数据要少得多。图片来源:P. Hassanzadeh/莱斯大学
有向图上的谐波分析及应用
我们针对定义在强连通有向图(有向图)顶点上的函数引入了一种新颖的谐波分析,其中随机游走算子是其基石。首先,我们将随机游走算子的特征向量集视为有向图上函数的非正交傅里叶型基。我们通过将从其狄利克雷能量获得的随机游走算子的特征向量变化与其相关特征值的实部联系起来,找到了一种频率解释。从这个傅里叶基开始,我们可以进一步进行并建立有向图的多尺度分析。我们提出了一种冗余小波变换和抽取小波变换,分别作为有向图的谱图小波和扩散小波框架的扩展。因此,我们对有向图的谐波分析的发展使我们考虑应用于有向图的半监督学习问题和图上的信号建模问题,突出了我们框架的效率。
有向图的对角化移位和过滤器
有大量数据是(或可以看作)由图的顶点索引的。例子包括生物网络、社交网络或互联网等通信网络 [1, 2]。为了将信号处理 (SP) 工具应用于此类图数据,包括移位、滤波器、傅里叶变换和频率响应在内的基本 SP 概念已被推广到图域 [3, 4],并构建了图信号处理 (GSP) 的基础。GSP 有两种基本变体。[4] 中的框架建立在代数信号处理 (ASP) [5] 的基础上,从邻接矩阵给出的移位定义中推导出这些概念。相比之下,[3] 将图拉普拉斯算子的特征基定义为图傅里叶基。用 ASP 术语来说,它选择拉普拉斯矩阵作为移位算子。无向图。这两种方法都为无向图提供了令人满意的 GSP 框架。也就是说,由于移位算子是对称的,因此存在一个酉傅里叶基。因此,移位以及所有滤波器(多项式
具有量子相位噪声的傅里叶变换量子相位估计
对于估计任意量子过程相位的基本任务,设计了一种基于傅里叶的量子相位估计变体,它使用多个纠缠量子比特的探测信号。对于简单的实际实现,每个探测量子比特都可以单独应用和测量。当量子比特最佳纠缠时,可以获得海森堡增强的估计效率缩放。相位估计协议可以在存在量子相位噪声的情况下同样应用。这使我们能够研究一般量子相位噪声对基于傅里叶的相位估计性能的影响。特别是,它揭示了在没有噪声的情况下发现的最佳策略随着噪声的增加逐渐失去其最优性。此外,与无噪声情况相比,在有噪声的情况下,纠缠的存在不再一致有利于估计;存在一个最佳纠缠量来最大化效率,超过该纠缠量就会变得有害。该结果有助于更好地了解量子噪声和纠缠,从而实现量子信号和信息处理。
傅立叶完全有界多项式的影响...
摘要:我们对 Arunachalam、Briët 和 Palazuelos (SICOMP'19) 的主要结果进行了新的介绍,并表明量子查询算法由一类新的多项式来表征,我们称之为傅里叶完全有界多项式。我们推测所有这样的多项式都有一个影响变量。这个猜想比著名的 Aaronson-Ambainis (AA) 猜想(计算理论'14)要弱,但对量子查询算法的经典模拟具有相同的含义。我们通过证明它适用于齐次傅里叶完全有界多项式来证明 AA 猜想的一个新案例。这意味着如果 d 查询量子算法的输出是 2 次 d 的齐次多项式 p,那么它有一个影响变量至少为 Var [ p ] 2。此外,我们给出了 Bansal、Sinha 和 de Wolf (CCC'22 和 QIP'23) 的结果的另一种证明,表明块多线性完全有界多项式具有影响变量。我们的证明更简单,获得更好的常数,并且不使用随机性。
费米子和玻色子的多体物理学简介 硕士 2 ICFP
2 平衡单粒子格林函数 9 2.1 格林函数的定义.....................................................................................................................................................................................................................................9 2.2 松原格林函数的性质....................................................................................................................................................................................................................................10 2.2.1 周期性和傅里叶级数....................................................................................................................................................................................................................10 . ... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ................................................................................................................................................................................................. 17 2.4.1 莱曼表示.................................................................................................................................................................................................... 17 2.4.2 希尔伯特变换....................................................................................................................................................................................... 17 2.4.2 希尔伯特变换....................................................................................................................................................................................................... 17 20 2.4.3 松原频率求和....................................................................................................................................................................................................................20 2.5 2 粒子相关函数....................................................................................................................................................................................................................................................................21