XiaoMi-AI文件搜索系统
World File Search SystemDMR 法规合规矩阵
以下是合规矩阵表,用于证明符合 DSA02 DMR 法规 2024 版。此合规矩阵旨在供需要遵守 DSA02 DMR 法规的组织使用。鼓励希望使用此合规矩阵的人下载并添加合规声明并保存为合规证据。无需将此合规矩阵返回给 DMR,它纯粹是作为一种辅助手段,方便组织轻松保持其合规性与最新法规保持一致。旨在根据法规新版本的发布每年更新和发布此矩阵。
WFM 技术价值矩阵™ 2024
由于控制成本仍然是组织的首要任务,劳动力管理为拥有大量一线和小时工的组织提供了减少因人员过剩、人员不足和人员流动而造成的损失的机会。在过去的一年里,领导者继续在人工智能和机器学习方面进行投资,特别是在预测能力和引入生成式人工智能虚拟助手方面。一线工人的生活质量改善也是一个重点,通信能力、轮班市场和表达轮班偏好的能力迅速成为首要任务。Nucleus 预计,随着客户重新评估当前解决方案所提供的价值,尤其是针对行业特定需求的价值,WFM 市场将在未来 18 个月内变得越来越具有竞争力。
带有图表符号的矩阵分化
矩阵差异(或矩阵演算)被广泛接受为各种领域的必不可少的工具,包括估计理论,信号处理和机器学习。这也用于量子信息理论的许多领域(例如,量子断层扫描[1],[2],量子系统的最佳控制[3]以及对纠缠否定性[4])的最佳控制。矩阵差异提供了一种方便的方法,可以相对于独立变量的每个组件,收集因变量的每个组件的衍生物,在这种情况下,因变量和自变量可以是标量,矢量或矩阵。然而,通常的矩阵(或索引)符号通常会避免繁琐的计算和困难的最直观解释。已知可以在线性代数中成功应用使用字符串图的图表表示(请参见[5]及其中的参考文献)。在本文中,我们提供了一种简单的图解方法,用于得出有用的矩阵差异公式。请注意,可以分别代表量子状态和量子过程的半半数矩阵和完全正面的图被视为Hermitian矩阵的真实希尔伯特空间中的载体和矩阵。在这里我们提到了一些相关的工作。参考。[6],呈现图形表示DEL操作员(即∇)的方式,其中计算仅限于三维欧几里得空间的情况。参考文献[7]提出了一个图表,用于操纵张量导数相对于一个参数。我们采用了与这些参考文献中给出的相似的表示法。
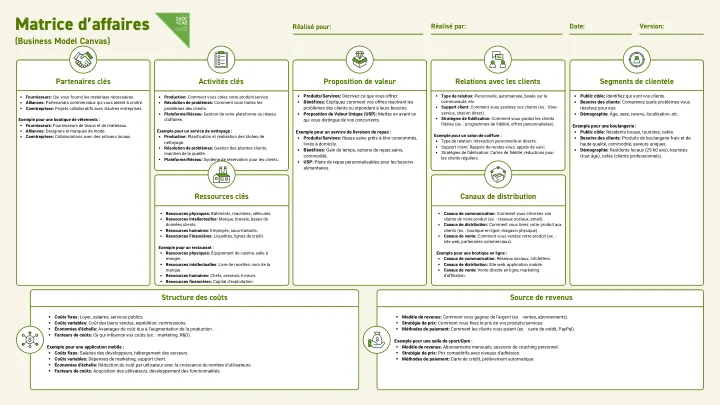
业务矩阵 - (商业模型画布)
忠诚度策略:忠诚度卡,定期客户减少。可变成本:出售商品的成本,运输,佣金。规模经济:由于生产的增加而带来的成本优势。通信渠道:如何告知客户产品(例如:社交网络,电子邮件)。
标准 ARM 计划矩阵内容
2. 房利美统一票据票据/附加条款表格参考 – 每份 ARM 必须使用在票据执行时有效的房利美统一票据/附加条款表格版本进行记录,或使用不包含任何与房利美统一票据/附加条款表格中规定的条款有重大差异的抵押贷款票据表格进行记录。如果未使用列中所示的房利美统一票据/附加条款表格或贷方使用任何其他非标准文件,则贷方须遵守销售指南的声明和保证条款和条件,包括但不限于 A2-2-03 中的文件保证条款。在不限制上述条款的情况下,抵押贷款票据必须规定按月分期付款,每笔付款的利息部分以 360 天为一年,并计算截至预定分期付款到期日的抵押贷款未偿还本金余额的 30 天利息。
改善来自微小培训的协方差矩阵...
大脑计算机界面域中使用的抽象脑电图数据通常具有低于标准的信噪比,并且数据采集很昂贵。有效且常用的分类器来区分事件相关电位是线性判别分析,但是,它需要对特征分布进行估计。虽然功能协方差矩阵提供了此信息,但其大量的免费参数要求使用正规化方法,例如Ledoit -Wolf收缩。假设与事件相关的潜在记录的噪声没有时间锁定,我们建议将与事件相关潜在数据的协方差矩阵分离,以进一步改善线性歧视分析的协方差矩阵的估计值。我们比较了三种正则变体和基于黎曼几何形状的特征表示,与我们提出的新型线性判别分析与时间耦合的协方差估计值进行了比较。对14个脑电图数据集的广泛评估表明,新颖的方法可将分类性能提高到小型训练数据集的最高四个百分点,并优雅地收敛于标准收缩率调查的LDA对大型培训数据集的性能。鉴于这些结果,该领域的从业人员应考虑使用线性判别分析来对事件相关的电位进行分类时,应考虑使用我们提出的时间耦合协方差估计,尤其是在很少有培训数据点可用时。
带扩展内存的小矩阵路径积分
最近,人们投入了大量精力来开发用于模拟凝聚相环境中量子力学过程动态的精确方法。这种兴趣主要受到量子信息理论的进步、1,2 对高效太阳能收集和传输的追求、3 以及对具有目标功能的纳米级设备进行优化设计的需求的推动。4 量子相干性在与多原子或凝聚相环境接触的系统动力学中的作用至关重要。由于量子力学相的微妙性质,评估干涉效应及其破坏需要有高精度、完全量子力学的模拟工具。在涉及孤立分子组装体或晶体介质中的自旋、电荷或能量传输的过程中,以及在高斯响应占主导地位的其他情况下,5 与可观测系统耦合的环境可以通过二次自由度很好地近似,从而产生系统浴哈密顿量 6
统计力学讲座集5:密度矩阵
Feynman代表Schrodinger量子力学的时间类似物,| ψ(t)⟩= ˆ u(t)| ψ(0)⟩用进化运算符ˆ u(t)= - i ˆ ht/ 1用路径 - 编写。