XiaoMi-AI文件搜索系统
World File Search System几乎
“逆转 CFIUS” 几乎终于
该行政命令实际上宣布了国家紧急状态，以应对“受关注国家”（在行政命令中定义为该行政命令附件中列出的国家，目前为中国、香港和澳门，但总统可能会在未来修改附件并更新受关注国家名单）构成的威胁，并规定设立由财政部管理的国家安全计划，以规范美国对这些国家从事“涉及对国家安全至关重要的三个领域的敏感技术的活动”的实体的某些投资：半导体和微电子、量子信息技术和人工智能（请参阅此处的白宫新闻稿）。具体而言，该行政命令要求财政部实施法规，以 1）要求美国个人提供与“受关注国家”上述行业某些交易相关的信息通知；2）禁止美国个人直接或间接参与“受关注国家”的某些其他交易，如本文详细讨论的那样。至于通知要求，目前似乎仅被视为一项通知，这与美国外国投资委员会管理的外国投资法规下针对具体案件的审查审批程序有很大区别。
（几乎）没有不良药物：药品几乎完全免于产品责任的解释
Sales of Bad Products，《纽约时报》（2010 年 10 月 26 日），https://perma.cc/6HFS-RKFH（上次访问时间为 2019 年 11 月 2 日）（报道制药巨头葛兰素史克在波多黎各经营的一家工厂生产受污染的抗抑郁药、糖尿病药物和胃酸反流药物）（存档于《华盛顿与李法律评论》）。5. 例如，参见 John LaMattina，《制药公司的声誉持续受损——可以做些什么来修复它？》 , F ORBES (2013 年 1 月 18 日，上午 8:27)，https://perma.cc/X4PY-YLB8（最后访问时间为 2019 年 11 月 2 日）（将制药行业声誉不佳的原因归咎于公司活动缺乏透明度以及优先考虑利润而非公平定价行为）（存档于《华盛顿与李法律评论》）。6. 例如，请参阅 Clifton Leaf 的《药物研发中的创新有多陈旧？想想：五年前的酸奶》，《财富》（2018 年 3 月 6 日），https://perma.cc/Y9A6-NDDN（最后访问时间为 2019 年 11 月 2 日）（指出，平均而言，30 家大大小小的生物科技公司 2017 年的收入中只有 11% 来自过去五年内开发的药物）（存档于《华盛顿与李法律评论》）；另见下文第 IV.D.1 部分（讨论投资者对新抗生素开发创新有限的失望）。 7. 这场危机尚未体现出该行业的责任感。参见 B ARRY M EIER，P AIN K ILLER：欺骗帝国与美国类固醇流行病的起源，第 155–72 页 (2018 年第 2 版)（证实了这一主张）；另见 Rebecca L. Haffajee 和 Michelle M. Mello，Drug Companies' Liability for the Opioid Epidemic，377 NEW E NG. J. M ED。 2301, 2305 (2017)（观察到“阿片类药物诉讼尚未对每年 130 亿美元的阿片类药物行业造成经济损失”，且阿片类药物诉讼“胜利均以和解的形式达成”）。另请参阅 Richard C. Ausness, 《阿片类药物诉讼的现状》，70 SCL R EV . 565 (2019)（对“阿片类药物诉讼”类案件进行了全面、最新的回顾，完全忽略了人身伤害诉讼，仅涉及政府发起的诉讼）；Anita Bernstein, 《沙利度胺的形成：大规模侵权行为作为毒性暴露的虚假治疗方法》，97 C OLUM . L. R EV . 2153 (1997)（得出结论，政府部门比人类原告更安全，他们的审慎和收钱权利不会受到攻击）；Jef Feeley，制药商不愿为解决阿片类药物泛滥提供资金；指望法庭胜诉，I NS . J.（2018 年 5 月 4 日），https://perma.cc/4AUP-YJST（上次访问时间为 2019 年 10 月 12 日）（解释说“制药公司并不急于为解决阿片类药物泛滥提供资金”，宁愿“在法庭上碰运气，也不愿支付数十亿美元来和解指责他们上瘾的诉讼”）（存档于《华盛顿与李法律评论》）。8. 参见 Alison Kodjak，民意调查：美国人支持政府采取行动抑制处方药价格，NPR（2019 年 3 月 1 日），https://perma.cc/K6EN-8SC8（上次访问时间为 2019 年 11 月 2 日）（讨论一项无党派民意调查，该调查的结论是“
几乎 α-F-收缩、不动点及其应用
不动点。借鉴 Berinde [3, 4]、Wardowski [23] 和 Samet 等人 [19] 的工作，我们熟悉了偏度量空间框架中的几乎 α - F 收缩和几乎 α - F 弱收缩，然后建立了单个不动点存在的充分假设。此外，受到分数阶非线性微分方程在众多科学和工程领域中具有重要意义的启发，我们应用我们的结果建立了满足周期性边界条件的分数阶微分方程的解。此外，受到聚光太阳能大量发电是最适合以合理方式缓解气候变化以及减少化石燃料消耗的技术之一的现实启发，我们解决了将太阳能转化为电能时出现的边界值问题。
从几乎光滑的空间到RCD空间
RCD条件，或更精确的两个参数K和N的RCD（K，N）条件是RICCI曲率下的下限的合成概念，并且是公制测量空间的尺寸上的上限。Special examples of metric measure spaces verifying the RCD( K, N ) condition, called RCD( K, N ) spaces , include Ricci limit spaces , which are by definition pointed Gromov-Hausdorfflimit spaces of complete Riemannian manifolds with Ricci curvature bounded below by K and dimension bounded above by N .The structure theory of Ricci limit spaces has been extensively studied in the frame- work of the Cheeger-Colding theory [ CC96 , CC97 , ChC00a , ChC00b ] (see also, for in- stance, [ CN15 , CJN21 ] for the more recent update), which establishes a regular-singular decomposition in terms of tangent cone analysis via splitting techniques.该理论不仅使我们在Riemannian几何形状中做出了巨大的决议（例如，在Anderson-Cheeger，Fukaya，Fukaya-Yamaguchi和Gromov的猜想中），而且在数量非碰撞环境中也尤其是在各个角色中都有明显的应用。值得注意的是，他们的理论在Fano歧管上的Kähler-Einstein指标的Yau-Tian-Donaldson Contecter证明中发挥了至关重要的作用[CDS15]，以及在可平稳的K-Moduli k-Moduli空间的k-Moduli k-Stable fano品种的k-Moduli空间[DS14，LWX19，LWX19，O15，SSY16]。RCD空间的理论可以被视为RICCI极限空间的最佳合成处理，并以两种方式开发了。另一个是使用基于dirichlet形式理论的γ-钙库来使用bakry-émery条件。第一个是使用曲率维度条件[LV09，ST06A，ST06B]来自最佳运输理论，以及Riemannian假设，称为In-Mally Hilbertianity，由[AGS14A，G15]提出的Hilbertianity。从[AGS15，AMS19，EKS15]中知道两种方法都是相同的，即可以通过完全不同的方式来表征/研究RCD空间。值得一提的是，RCD理论的显着应用已经在其他几何形状上找到了[BMS22]，即[KLP21]，关于Alexandrov几何形状中存在许多无限期的大地测量学。请注意，Cheeger-Colding理论纯粹是局部特征，但是根据定义，RCD理论需要全球信息。因此，给出RCD空间的局部表征是一个有趣的问题。在许多感兴趣的情况下，在示例中，人们处理的空间几乎是平稳的，即，大粗略的空间是通过在下面界定的ricci的光滑的riemannian歧管给出的空间，其奇异集的奇异集具有很高的hausdorsimensimension。精确的定义将在第1.3小节中解释（对于更一般的加权空间，定义为4.13）。该问题然后减少到在单数集中施加适当的条件（另请参见[BKMR21]）。在许多几何环境中，几乎光滑的空间起着重要的作用，例如，汉密尔顿 - 蒂恩猜想的证明[CW17，BA16]，以及Kähler-Einstein关于奇异品种的指标的研究（例如，参见[CCHSTT25，SO14，SZ24，SZ24，GS25]）。在下一个小节中，让我们解释我们将采用的统一地方条件是什么。在本文中，我们将为RCD空间提供几乎光滑的空间（包括加权空间）的特征。我们的标准将以统一的局部条件为例，并且允许空间是非紧凑的。
相互作用的电子几乎紧密的TROTTERTION
我们考虑在数字量子计算机上模拟量子系统。我们表明，通过同时利用目标汉密尔顿的交换性，相互作用的稀疏以及初始状态的先验知识，可以通过利用量子模拟的性能来提高量子模拟的性能。我们实现了涵盖各种物理系统的一类相互作用的电子（包括平面波 - 巴西电子结构和费米 - 哈伯德模型）的动力化。我们通过在η-电子歧管中嵌套术语的嵌套换向器来估计模拟误差。我们开发了多种技术来界定一般费米子操作员的转移幅度和期望，这可能是独立的。我们表明，它可以使用N 5/3η2 / 3 + N 4/3η2 / 3 N O（1）< / div>
平行和（几乎）工作有效的动态编程
Bellman在1950年代提出的动态编程（DP）的思想是最重要的算法技术之一。并行，许多基本和顺序简单的问题变得更具挑战性，并且对（几乎）工作有效的解决方案开放（即，与最佳顺序解决方案相比，最多是polygarogarithmic因子的工作）。实际上，顺序的DP al-gorithms采用许多高级优化，例如决策单调性或特殊数据结构，并且比直接解决方案获得更好的工作。许多这样的优化是不依次的，这为并行算法带来了额外的挑战，以实现相同的工作。本文的目的是通过平行经典，高度优化和实用的顺序算法来实现（几乎）（几乎）工作效率的ALLEL DP算法。我们显示了一个名为“ Cordon算法”的通用框架，用于并行DP算法，并使用它来解决一些经典问题。我们选择的问题包括最长增加的子序列（LIS），最长的常见子序列（LCS），凸/凹面最小重量亚序列（LWS），最佳字母树（OAT）等。我们展示了如何使用Cordon算法来实现与顺序算法相同的优化水平，并获得良好的并行性。我们的许多算法在概念上都很简单，我们将一些实验结果作为概念证明。
重大失误：AI 将取代几乎所有东西
AI 将以惊人的速度取代白领工作。1 关于 AI 将如何影响“边缘”就业的承诺具有误导性。这将是一次直接打击，尽管所有炸弹爆炸需要几年时间。事实上，关于 AI 将产生的影响，唯一不确定的是影响何时到来。毫无疑问，它将消灭越来越多的工作。专业人士小心翼翼地向他们保证他们的工作和职业不会受到 AI 的威胁，这是欺骗性的。在最坏的情况下，它们是危险的，因为每个人都需要利用尽可能多的信息来规划他们的职业未来，而公司需要制定战略，以优化这一代人中最强大技术的应用。确信 AI 不会抢走他们的工作或商业模式，这是错误的。AI 会抢走他们所有人的饭碗。
儿童死亡和几乎死亡评估生效日期
J＆B医疗是由知识渊博的行业专业人士组成的全国认证的妇女企业。J＆B医疗的热情团队成员有动力在每次互动时提供出色的服务。我们的目标很简单：提高生活质量，改善临床结果并降低医疗保健成本。J＆B医疗无非是最具创新性的行业实践和最高水平的完整性。
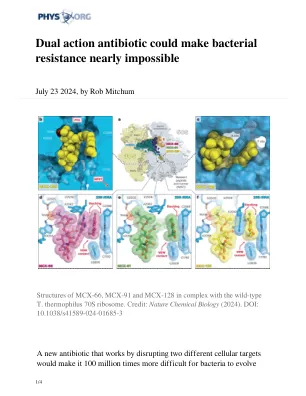
双重作用抗生素可以使细菌抗性几乎不可能
“这种抗生素的美在于它通过细菌中的两个不同靶标杀死，” UIC的杰出药物科学教授亚历山大·曼金（Alexander Mankin）说。“如果抗生素以相同的浓度击中两个靶标，则细菌通过在两个靶标中的任何一个中的随机突变获得抗药能力而失去了抗性的能力。”