XiaoMi-AI文件搜索系统
World File Search System印度理工学院鲁尔基分校
印度理工学院鲁尔基分校 系别:应用数学与科学计算系 科目代码:AMC-501 课程名称:应用优化技术 LTP:3-0-0 学分:3 学科领域:PCC 课程大纲:优化简介、凸集、凸函数、数学建模、线性规划:图解法、单纯形法、线性规划中的对偶性、灵敏度分析、对偶单纯形法、整数规划问题、混合整数规划问题、无约束优化 - 牛顿-拉夫逊法、拟牛顿法、共轭梯度法、最速下降法、约束优化 - 拉格朗日法、广义递减梯度法、罚函数法、多目标优化 - 多目标优化问题、帕累托前沿、支配和非支配解、经典多目标优化方法(如加权和方法、e-约束方法)。
控制与仪表工程
16MA607 数值方法与优化 4 - 0 - 0 - 4 方程和特征值问题的解:线性插值法、假位置法、牛顿法、不动点定理陈述、不动点迭代、高斯消元法解线性系统、高斯-约登法和迭代法、高斯-约登法求矩阵逆、幂法求矩阵特征值。常微分方程的初值问题:单步法、泰勒级数法、欧拉法和修正欧拉法、用于解一阶和二阶方程的四阶龙格-库塔法。多步法:Milne 和 Adam 的预测器和校正器方法。线性规划:公式化、图形和单纯形法、大 M 方法、两相法、对偶单纯形法、原始对偶问题。无约束一维优化技术:必要和充分条件。无限制搜索方法:斐波那契和黄金分割法、二次插值法、三次插值和直接根法。无约束 n 维优化技术:直接搜索法、随机搜索、模式搜索和 Rosen Brooch 的山丘声称法、下降法、最速下降法、共轭梯度法、拟牛顿法。约束优化技术:必要和充分条件、等式和不等式约束、Kuhn-Tucker 条件、梯度投影法、割平面法、罚函数法。动态规划、最优化原理、递归方程方法、最短路线应用、货物装载、分配和生产计划问题。教科书/参考文献:1.S. S. Rao,“能源优化理论与实践”,John Wiley and Sons,2009 年。2.Taha H. A.,“运筹学——导论”,第八版,Prentice Hall
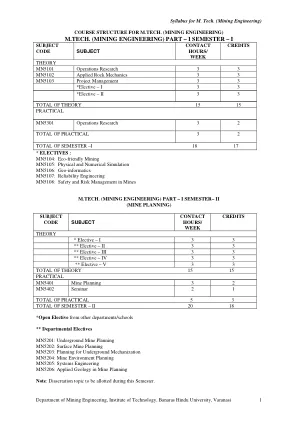
M.TECH.(采矿工程)部分 - 瓦拉纳西
M.TECH.(采矿工程)第一部分第一学期 MN5101:运筹学(3 个学分)运筹学简介基本概念。线性规划单纯形法、对偶问题和后最优性分析。动态规划概念、递归方程方法、计算程序、正向和反向计算以及维数问题。网络分析网络表示、关键路径计算、项目调度中的概率和成本考虑、时间表的构建和资源平衡。库存模型定义、确定性和概率模型。排队论基本概念、到达和离开的公理推导、泊松队列的分布、泊松排队模型、非泊松排队模型、具有服务优先级的排队模型。非线性规划无约束外部问题、约束外部问题、规划 - 可分离、二次、随机和几何。 MN5102:应用岩石力学(3 学分)地应力地壳中的地应力。地应力测定方法。矿井开口周围的应力各种形状的矿井开口周围的应力分布。矿井开口和矿柱的设计支架设计岩石锚杆、锚索、顶板封堵、喷射混凝土、房柱支撑和长壁工作面。采空区支撑崩落和填充力学。岩爆和冲击机制、预测和控制。沉降机制、预测和控制。竖井柱设计。
ENCS 课程描述
ENCS 课程描述 ENCS 5300. 纳米材料基础 (3):本课程重点介绍描述和解释纳米级物质特性的化学、物理和数学概念。它将强调理解自组装过程背后的分子驱动力以及用于表征所得纳米材料的方法所需的基本化学、物理和数学。它还将介绍纳米材料的应用。 ENCS 6010. 高级应用数学 (3):本课程涵盖高级数学主题,包括线性代数、数值方法、傅里叶分析、离散数学、概率和统计以及代数结构,特别强调在工程和计算科学中的应用。 ENCS 6020. 高级计算 (3):本课程提供在高端计算机、计算机网络或个人计算机上进行计算的基本知识、技能和工具。主题包括:编程和编程语言;数据结构、算法和计算复杂性;高性能计算;分布式计算;优化;统计数据分析;计算误差分析。还将介绍先进计算技术的选定工程应用。 ENCS 6030. 网络物理系统的建模与仿真 (3):研究建模、仿真和设计的原理,包括制定规范和对由彼此通信并通过传感器和执行器与物理世界交互的设备组成的网络物理系统进行分析。主题包括同步和异步模型以及定时模型、安全性和活跃性要求以及实时调度。还研究了动态系统和混合系统的建模和仿真的一些方面。 ENCS 6110. 先进机器人系统 (3):本课程主要介绍机器人变换、运动学、动力学、差分运动、运动和路径规划、操纵和移动控制。高级主题包括:多机器人系统合作和协作任务规划和执行、机器人传感器接口和集成、被动和主动感知、处理和推理。学生将有机会通过实验室动手项目了解机器人软件、传感器和硬件。ENCS 6120。机电一体化系统设计 (3):本课程旨在涵盖从机电一体化理论的初步知识到基于项目的机电一体化系统设计。本课程的多学科内容包括:机制、电子、传感器、控制策略以及控制环路中的软件、固件和硬件。本课程还讨论了将机电一体化系统与传感器、机器人系统、可编程逻辑控制器 (PLC) 和人机界面集成的技术和技能。成功完成本课程的学生应能够解决需要紧密集成机电一体化组件和子组件以支持嵌入式机电机构和控制系统的多学科工程设计项目。ENCS 6200。工程设计优化 (3):优化技术的计算机化设计方法。使用设计变量和约束制定优化问题。使用数学模型解决问题,运筹学中的确定性优化方法,线性规划模型,单纯形法,线性规划中的对偶性和灵敏度。非线性优化和多目标函数优化,约束和无约束问题。
空间高效的内点法,应用于线性规划和最大权重二分匹配
是计算机科学和运筹学中最基本的问题之一。在过去的半个世纪里,人们致力于开发时间高效的线性规划求解器,例如单纯形法 [23]、椭球法 [44] 和内点法 [41]。近几年,利用内点法 (IPM) 加速线性规划求解得到了深入研究 [20, 55, 13, 35, 65, 25, 71]。当 m ≈ n 时,最先进的 IPM 运行时间为 O(m2+1/18+mω),当 m≫n 时,运行时间为 O(mn+n3)。为了实现这些令人印象深刻的改进,大多数此类算法利用随机和动态数据结构来同时维护原始解和对偶解。虽然这些算法在时间上是高效的,但它们不太可能以空间高效的方式实现:维护原始对偶公式需要 Ω(m + n2) 空间,当 m ≫ n 时尤其不能令人满意。在本文中,我们研究了在流式模型中求解线性规划的问题:在每一遍中,我们可以查询 A 的第 i 行和 b 的对应行。目标是设计一个既节省空间又节省遍历次数的 LP 求解器。所谓高效,我们的目标是获得一种不依赖于 m 的多项式的算法,或者更具体地说,我们提出一个健壮的 IPM 框架,该框架仅使用 e O(n2) 空间和 e O(√n log(1/ϵ)) 次遍历。1据我们所知,这是实现与 m 无关的空间和遍历最高效的流式 LP 算法。目前最好的 LP 流式算法要么需要 Ω(n) 次传递,要么需要 Ω(n2+m2) 空间来进行 O(√n) 次传递。对于高密集 LP(m≫n)的情况,我们的算法实现了最佳空间和传递。获得这些 LP 算法的关键因素是从时间高效的原始对偶 IPM 转变为时间效率较低的仅对偶 IPM [64]。从时间角度来看,仅对偶 IPM 需要 e O(√nlog(1/ϵ)) 次迭代,每次迭代可以在 e O(mn+poly(n)) 的时间内计算完成。然而,它比原始对偶方法更节省空间。具体而言,我们表明每次迭代,只需维护一个 n×n 的 Hessian 矩阵即可。为了获得 e O ( √ n log (1 /ϵ )) 次传递,我们证明了诸如 Lewis 权重 [ 56 , 21 ] 等非平凡量可以以仅使用 e O ( n 2 ) 空间的就地方式递归计算。既然我们有了用于流式模型中一般 LP 的空间和传递效率高的 IPM,我们将使用半流式模型中的图问题应用程序对其进行实例化。在半流式模型中,每条边及其权重都以在线方式显示,并且可能受到对抗顺序的影响,并且算法可以在 e O ( n ) 空间中对流进行多次传递。2我们特别关注最大权重二分匹配问题,其中带有权重的边以流式传输给我们,目标是找到一个匹配,使其中的总权重最大化。虽然对这个问题的研究已经很多([ 2 , 36 , 24 , 3 , 9 ] 等),但大多数算法只能计算近似匹配,这意味着权重至少是最大权重的 (1 − ϵ )。对于精确匹配的情况,最近的一项研究 [ 6 ] 提供了一种算法,它取 n 4 / 3 + o (1)