机构名称:
¥ 2.0
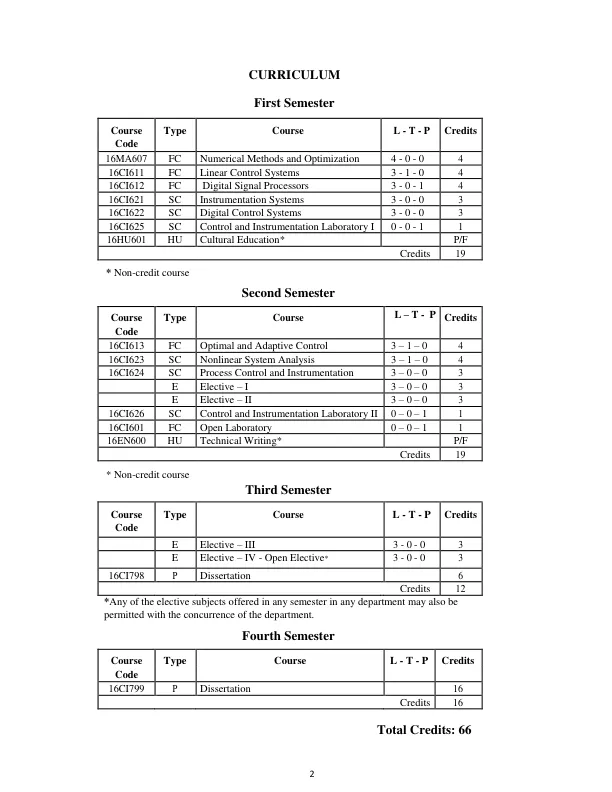
16MA607 数值方法与优化 4 - 0 - 0 - 4 方程和特征值问题的解:线性插值法、假位置法、牛顿法、不动点定理陈述、不动点迭代、高斯消元法解线性系统、高斯-约登法和迭代法、高斯-约登法求矩阵逆、幂法求矩阵特征值。常微分方程的初值问题:单步法、泰勒级数法、欧拉法和修正欧拉法、用于解一阶和二阶方程的四阶龙格-库塔法。多步法:Milne 和 Adam 的预测器和校正器方法。线性规划:公式化、图形和单纯形法、大 M 方法、两相法、对偶单纯形法、原始对偶问题。无约束一维优化技术:必要和充分条件。无限制搜索方法:斐波那契和黄金分割法、二次插值法、三次插值和直接根法。无约束 n 维优化技术:直接搜索法、随机搜索、模式搜索和 Rosen Brooch 的山丘声称法、下降法、最速下降法、共轭梯度法、拟牛顿法。约束优化技术:必要和充分条件、等式和不等式约束、Kuhn-Tucker 条件、梯度投影法、割平面法、罚函数法。动态规划、最优化原理、递归方程方法、最短路线应用、货物装载、分配和生产计划问题。教科书/参考文献:1.S. S. Rao,“能源优化理论与实践”,John Wiley and Sons,2009 年。2.Taha H. A.,“运筹学——导论”,第八版,Prentice Hall
控制与仪表工程
主要关键词