XiaoMi-AI文件搜索系统
World File Search System参数空间
SAM-PARSER：通过参数空间重构高效微调 SAM
任意分割模型 (SAM) 因提供强大且通用的图像对象分割解决方案而备受关注。然而，在不同场景下对 SAM 进行微调以用于下游分割任务仍然是一个挑战，因为不同场景的不同特征自然需要不同的模型参数空间。大多数现有的微调方法试图通过引入一组新参数来修改 SAM 的原始参数空间，以弥合不同场景之间的差距。与这些工作不同，在本文中，我们提出通过参数空间重构（SAM-PARSER）来有效地对 SAM 进行微调，其在微调过程中引入几乎为零的可训练参数。在 SAM-PARSER 中，我们假设 SAM 的原始参数空间相对完整，因此它的基能够重建新场景的参数空间。我们通过矩阵分解获得基，并通过基的最佳线性组合对系数进行微调以重建适合新场景的参数空间。实验结果表明，SAM-PARSER 在各种场景中表现出卓越的分割性能，同时与当前参数高效的微调方法相比，可训练参数的数量减少了约 290 倍。
空间的多维参数空间划分...
数值模拟通常用于理解给定时空现象的参数依赖性。对多维参数空间进行采样并运行相应的模拟将产生大量时空模拟运行的集合。分析集合的主要目的是将多维参数空间划分（或分割）为具有相似行为的模拟运行的连通区域。为了促进这种分析，我们提出了一种用于多维参数空间分区的新型可视化方法。我们的可视化基于超切片器的概念，它允许不失真地查看参数空间段的范围和转换。对于参数空间内的导航，支持与参数空间样本的 2D 嵌入（包括它们的段成员资格）的交互。通过分析集合模拟运行的相似性空间，以半自动方式生成参数空间分区。相似模拟运行的集群会诱导参数空间分区的段。我们将参数空间分区可视化与集成模拟运行的相似空间可视化相链接，并将它们嵌入到交互式可视化分析工具中，该工具支持对时空模拟集成的所有方面的分析，其总体目标是分析参数空间分区。然后可以对分区进行可视化分析和交互式细化。我们将我们的方法与其他方法进行了比较，并与来自三个不同领域的案例研究中的专家一起对其进行了评估。© 2022 Elsevier BV 保留所有权利。
![arXiv:2304.13927v1 [cond-mat.mtrl-sci] 2023 年 4 月 27 日](/simg/g:\will\search\icon\source\f\f5241edb25c45210e6306a97c2c12dcb8a000883.webp)
arXiv:2304.13927v1 [cond-mat.mtrl-sci] 2023 年 4 月 27 日
取决于搜索空间的类型。如果考虑连续参数空间，则 D = { xi } i =1 ,...,N
使用人工磁场和配备机器人激光的手臂进行超级kamiokande pmts表征探测用机器学习武装的顽固性BSM参数空间
这项研究引入了创新的机器学习（ML）辅助采样方法，旨在更有效地扩展标准模型（BSM）参数空间。Markov Chain Monte Carlo（MCMC）和Hamiltonian Monte Carlo（HMC）等传统方法经常在高维，多模式空间中面临限制，从而导致计算瓶颈。我们的方法结合了积极训练的深层网络（DNN）和嵌套采样，动态预测更高的样子区域，以加速收敛并提高采样精度。这些可扩展的框架具有可扩展的框架，可以在高层物理学（HEP）研究中进行全面分析，以解决bsm compariete bsm commiate bsm commiate bsm compariate bsm compariate bsm comporiate comportiation comportiation comportiation。
主动脉“疾病中的疾病”
摘要在本文中，我们介绍了统计学习问题的新方法Argminρ（θ）∈PθW2 Q（ρ（ρ（θ）））在量子L 2-量子l 2- w insetrim l 2- w inserric中。我们通过考虑使用维度二维C ∗代数的密度算子的Wasserstein天然梯度流来解决此估计问题。对于密度运算符的连续参数模型，我们拉回了量子瓦斯汀公制，以使参数空间与量子Wasserstein Information Matrix成为Riemannian歧管。使用Benamou -Brenier公式的量子类似物，我们在参数空间上得出了自然梯度流。我们还通过研究相关的Wigner概率分布的运输来讨论某些连续变量的量子状态。
量子统计学习通过量子瓦斯坦天然梯度
摘要在本文中，我们介绍了统计学习问题的新方法Argminρ（θ）∈PθW2 Q（ρ（ρ（θ）））在量子L 2-量子l 2- w insetrim l 2- w inserric中。我们通过考虑使用维度二维C ∗代数的密度算子的Wasserstein天然梯度流来解决此估计问题。对于密度运算符的连续参数模型，我们拉回了量子瓦斯汀公制，以使参数空间与量子Wasserstein Information Matrix成为Riemannian歧管。使用Benamou -Brenier公式的量子类似物，我们在参数空间上得出了自然梯度流。我们还通过研究相关的Wigner概率分布的运输来讨论某些连续变量的量子状态。
以排为中心的控制在信号交叉点上建立在混合MPC系统，在线学习和分布式优化第II部分：理论分析
多项式方程的参数化系统在科学和工程的许多范围内都会出现，例如，动态系统的平衡，链接满足设计约束的链接，并在compoter视觉中进行场景重建。由于不同的参数值可以具有不同的实际解数，因此参数空间被分解为边界形成真实判别基因座的区域。本文认为将真实的判别基因座定位为机器学习中的超级分类问题，目的是确定参数空间上的分类边界，其中类是真实解决方案的数量。该艺术提出了一种新型的采样方法，该方法仔细采样了多维参数空间。在每个样本点，同型延续用于获取相应多项式系统的实际解数。机器学习技术在内，包括最近的邻居，支持向量分类器和神经网络可有效地近似实际的判别基因座。学习了真正的判别基因座的一种应用是开发一种实际同义方法，该方法仅跟踪实际解决方案路径，与传统方法不同，该方法跟踪所有复杂的解决方案路径。示例表明，所提出的方法可以很好地近似复杂的解决方案边界，例如Aris-
通过组合测试挑战自治
摘要 - 本文描述了一种称为仙人掌的输入空间建模和测试生成方法（具有组合测试的挑战性自治），该方法为自主系统创建了一系列“挑战场景”。尽管自主系统的参数空间是广泛的，但仙人掌有助于使用组合测试以及通过将专家判断到场景的制定中减少参数空间。可以在适当的测试基础结构（例如模拟器或循环测试）上执行所得场景。仙人掌可用于锻炼系统，作为获得符合ISO 21448或UL 4600等标准的努力的一部分。该方法用于生成商用自动驾驶汽车感知系统的测试方案。索引术语 - 跨越测试，输入建模，Au ossos Systems，自动驾驶汽车
贝叶斯推理的计算技术
统计计算很大程度上由概率的加权总和或积分组成。贝叶斯推论和频繁统计之间的关键实际差异之一是，在将这些竞争性的方法解决相同问题的情况下出现了巨大不同类型的积分类型（Loredo 1992）。例如，考虑到某些观察到的数据d，估计某些模型的参数m；用θ共同表示参数。在贝叶斯和频繁的积分中出现的关键数量是假设模型为真的数据并假定要知道的参数的概率，p（d |θ，m）。被认为是数据的函数，这称为采样分布；作为参数的函数，它称为可能性函数，它将缩写为l（θ）。该方法之间的基本实际差异是，频繁计算需要在数据维度（样本空间）上进行此数量的积分，而贝叶斯计算需要在参数空间上进行积分。基于通过参数空间进行求和或集成在试图使用样品空间中计算的概率进行推断的概率的概率上的推断。在这里的简短空间中，对这些优势的重要讨论是不可能的。必须提及两个具有巨大实际实用性的积极优势。在贝叶斯推理中，可以直接消除滋扰参数，同时简单地通过在φ上整合（ψ，φ）的关节分布来解决它们的不确定性。首先，在绝大多数的实际应用中，参数空间可以分为两个部分θ=（ψ，φ），其中兴趣集中在ψ上，并且φ由对数据建模但不感兴趣的“滋扰”参数组成（例如，背景强度）。没有完全的SAT-
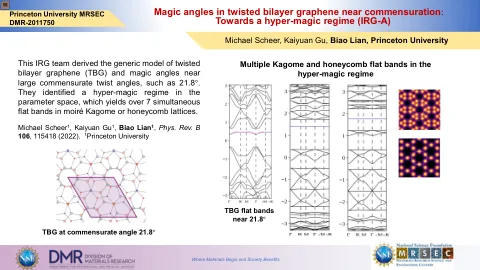
迈向超魔法制度（IRG-A）
这个IRG团队得出了扭曲的双层石墨烯（TBG）的通用模型和大型相称的扭曲角（例如21.8°）附近的魔法角度。他们确定了参数空间中的超魔法制度，该方案在MoiréKagome或Honeycomb lattices中产生了超过7个同时的平坦带。