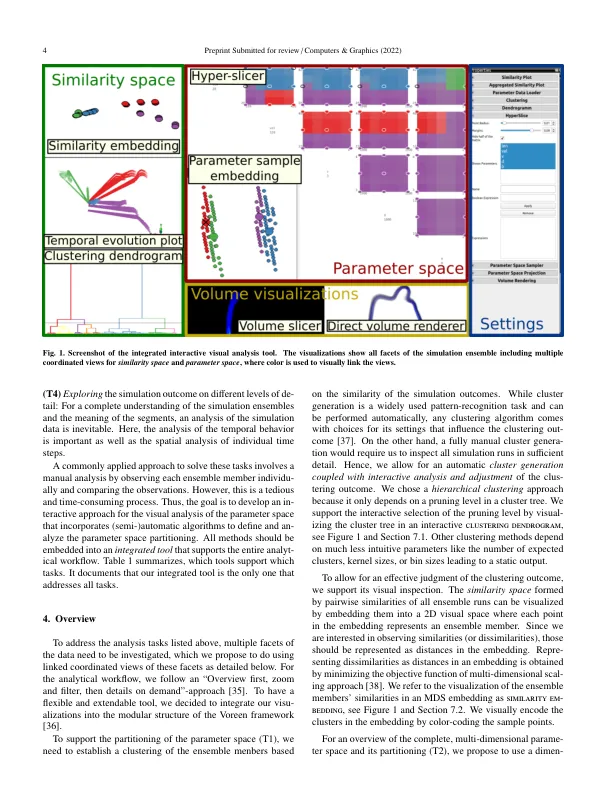
数值模拟通常用于理解给定时空现象的参数依赖性。对多维参数空间进行采样并运行相应的模拟将产生大量时空模拟运行的集合。分析集合的主要目的是将多维参数空间划分（或分割）为具有相似行为的模拟运行的连通区域。为了促进这种分析，我们提出了一种用于多维参数空间分区的新型可视化方法。我们的可视化基于超切片器的概念，它允许不失真地查看参数空间段的范围和转换​​。对于参数空间内的导航，支持与参数空间样本的 2D 嵌入（包括它们的段成员资格）的交互。通过分析集合模拟运行的相似性空间，以半自动方式生成参数空间分区。相似模拟运行的集群会诱导参数空间分区的段。我们将参数空间分区可视化与集成模拟运行的相似空间可视化相链接，并将它们嵌入到交互式可视化分析工具中，该工具支持对时空模拟集成的所有方面的分析，其总体目标是分析参数空间分区。然后可以对分区进行可视化分析和交互式细化。我们将我们的方法与其他方法进行了比较，并与来自三个不同领域的案例研究中的专家一起对其进行了评估。© 2022 Elsevier BV 保留所有权利。