XiaoMi-AI文件搜索系统
World File Search System同构
![arxiv：2402.06946v1 [Quant-ph] 2024年2月10日](/simg/g:\will\search\icon\source\e\e94345c8e3a46ec45b4a0f221fb0d84eba7d5223.webp)
arxiv：2402.06946v1 [Quant-ph] 2024年2月10日
cz）门是构造通用门的基础元素，包括受控门。我们首先要解释量子过程的理论（QPT），探索Choi-Jamiolkowski同构或量子过程的CHOI矩阵表示，以及使用CHOI表示的QPT算法。随后，我们使用基于Transmon的超导量子量子计算机对SQSCZ Gate的实验实现提供了详细的见解。为了全面评估嘈杂的中间量子量子（NISQ）计算机上门的性能，我们使用IBM量子的模拟器和IBM量子的真实Quantum计算机进行了跨不同环境的QPT实验。在我们的QPT实验中利用CHOI矩阵可以全面表征我们的量子操作。我们的分析揭示了SQSCZ门的值得称赞的保真度和噪声特性，过程保真度达到97。27098％和88。99383％，分别是分数。这些发现对量子计算领域中的理论理解和实际应用具有有希望的含义。
量子通道的阴影过程断层扫描
量子过程断层扫描是构建量子计算机，启用量子网络并了解量子传感器的关键能力。像量子状态断层扫描一样，任意量子通道的过程层析成像需要多个测量值，这些测量值在量子位的数量中呈指数缩放。然而，应用于量子状态的影子tomog-raphy的最新领域已经证明了能够提取有关状态的关键信息的能力。在这项工作中，我们将影子状态断层扫描的概念应用于表征量子过程的挑战。我们利用Choi同构直接将严格的界限从阴影状态层析成像到阴影过程断层扫描中，并且在过程断层扫描中独有的测量数量上找到了其他界限。我们的结果，包括用于实现阴影过程刻度的算法，启用新技术，包括评估通道串联以及将通道应用于量子状态的阴影。这为理解大规模量子系统提供了巨大的改进。
![arXiv:2301.03880v1 [cond-mat.str-el] 2023 年 1 月 10 日](/simg/g:\will\search\icon\source\3\312a1cae25beda5f155ead558fb0933088632887.webp)
arXiv:2301.03880v1 [cond-mat.str-el] 2023 年 1 月 10 日
AMX 3 化合物结构多样，一个显著的例子是后钙钛矿结构，它采用具有共角和共边八面体的二维框架。已知的分子后钙钛矿很少，其中尚未报道过磁性结构。本文我们报告了分子后钙钛矿的合成、结构和磁性：CsNi(NCS) 3 ，一种硫氰酸酯框架，以及两种新的同构类似物 CsCo(NCS) 3 和 CsMn(NCS) 3 。磁化测量表明这三种化合物都具有磁序。CsNi(NCS) 3（居里温度，TC = 8.5 (1) K）和 CsCo(NCS) 3（TC = 6.7 (1) K）为弱铁磁体。另一方面，CsMn(NCS) 3 属于反铁磁体（Néel 温度，TN = 16 . 8 ( 8 ) K）。CsNi(NCS) 3 和 CsMn(NCS) 3 的中子衍射数据显示，两者都是非共线磁体。这些结果表明，分子框架为实现下一代信息技术所需的自旋结构奠定了坚实的基础。
可以安全地讲述您的故事吗？为了实现敏感叙事的隐私
过去二十年来，在开发隐私技术进行数据分析方面发生了爆炸。加密技术，例如完全同构加密和安全的多方计算（例如（Gentry，2009; Ben-Or等人，1988年； Chaum等。，1988年））为如何委派，处理和组合私人定量数据创造了丰富的选择 - 而没有不必要地揭示潜在的细节。定义和基础工作，例如差异隐私的开发（Dwork等，2006年）及其实际部署（例如（局等人，2023年））为隐私保护设定了新的高标准，使我们能够在不牺牲个人的情况下为数据科学的集体利益带来。但是 - 人们最终不是数字。叙事才能让我们感到被听到和被听到，并恢复情感深度，以使经验被变成数字和分类表示。我也是如此的运动表明了个人叙事在将广泛的体验带到揭示的方式上，以纯数字无法实现的方式。这种权力通常会以巨大的风险行使 - 包括对幸存者的风险
研究论文 使用反向传播神经网络对高光谱遥感数据中的岩性信息进行提取和分类
为了解决高光谱遥感数据处理中遇到的同构问题,提高高光谱遥感数据在岩性信息提取与分类的精度,以岩石为研究对象,引入反向传播神经网络(BPNN),对高光谱图像数据进行归一化处理后,以岩性光谱与空间信息为特征提取目标,构建基于深度学习的岩性信息提取模型,并使用具体实例数据分析模型的性能。结果表明:基于深度学习的岩性信息提取与分类模型总体精度为90.58%,Kappa系数为0.8676,能够准确区分岩体性质,与其他分析模型相比具有较好的性能。引入深度学习后,提出的BPNN模型与传统BPNN相比,识别精度提高了8.5%,Kappa系数提高了0.12。所提出的提取及分类模型可为高光谱岩矿分类提供一定的研究价值和实际意义。
使用椭圆曲线的隐私投票系统
投票是民主的基石，需要确保安全，透明度和选民匿名的系统。传统投票方法通常面临诸如篡改和缺乏机密性之类的挑战，促使人们需要安全的数字解决方案。本文使用椭圆曲线密码学（ECC）提出了一个隐私的投票系统，以解决这些问题[1]。ECC是一种有效的加密技术，可提供较小的钥匙尺寸的强度安全性，使其非常适合可扩展系统。它确保了安全的沟通并保护选民身份[2]。将ECC与区块链技术整合在一起，进一步通过分散的信任和不可变化的存储提高了数据完整性和透明度，如所示。同构加密用于启用加密票的计算，以确保选民在Tallying期间的私密性[3]。通过将ECC，区块链和同质加密结合起来，拟议的系统解决了电子投票中的关键问题，例如数据操纵和双重投票，同时保持选民的保密性和可信度[4]。2。文学评论
重新访问BGV和BFV
摘要。同构加密中的许多应用都需要将密文的插槽移至不同密文的系数。对于BGV和BFV方案，在非电动环环环的情况下，提出了实现此插槽到循环转换的唯一有效算法。在本文中，我们设计了一种类似FFT的方法，用于分解插槽到循环的转换（及其倒数），以进行两次环形环。所提出的方法可以完全和稀疏的包装插槽处理。我们的算法降低了从线性到对数数量的FHE操作数量的插槽到循环转换的计算复杂性，这通过详细的复杂性分析显示。新程序是在BFV的Microsoft Seal中实现的。实验报告了从GF（8191 8）中包装2个12个元素时，最高44倍的加速度。我们还研究了一个完全包装的自举操作，该操作从GF（65537）中刷新2 15个元素，并获得12倍的摊销速度。
论量子比特 Clifford 层次结构中的群
这里我们研究了可以使用量子比特 Clifford 层次结构中的元素构造的酉群。我们首先提供半 Clifford 和广义半 Clifford 元素必须满足的必要和充分规范形式才能进入 Clifford 层次结构。然后我们对可以由这些元素形成的群进行分类。直到 Clifford 共轭，我们对 Clifford 层次结构中可以使用广义半 Clifford 元素构造的所有此类群进行分类。我们在附录中讨论了此分类的一个可能的小例外。这可能不是对量子比特 Clifford 层次结构中所有群的完整分类，因为目前尚不清楚 Clifford 层次结构中的所有元素是否都必须是广义半 Clifford。除了 Cui 等人发现的对角门群之外，我们还表明 Clifford 层次结构中还包含许多非同构（对角门群）广义对称群。最后，作为此分类的应用，我们研究了由本文列举的群的结构给出的横向门的限制，这可能具有独立的兴趣。
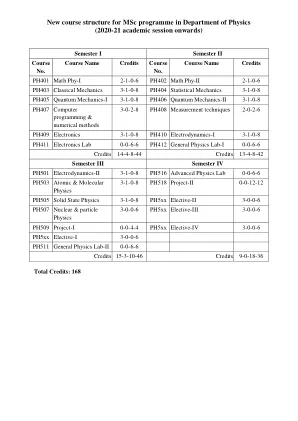
物理系理学硕士课程的新课程结构
PH401：数学物理 I (2-1-0-6) 线性代数：线性向量空间：对偶空间和向量、柯西-施瓦茨不等式、实数和复数向量空间的定义、度量空间、线性算子、子空间；跨度和线性独立性：行减少和方法；基础和维度：使用简化的跨度和独立性测试 (RREF) 方法；线性变换：图像、核、秩、基础变换、转移矩阵、同构、相似变换、正交性、Gram-Schmidt 程序、特征值和特征向量、希尔伯特空间]。张量：内积和外积、收缩、对称和反对称张量、度量张量、协变和逆变导数。常微分方程和偏微分方程：幂级数解、Frobenius 方法、Sturm-Liouville 理论和边界值问题、格林函数；笛卡尔和曲线坐标系中不同波动方程的分离变量法，涉及勒让德、埃尔米特、拉盖尔和贝塞尔函数等特殊函数以及涉及格林函数的方法及其应用。教材：
使用单个预共享键
无条件安全性意味着对加密文本的知识没有提供有关相应宣传的任何信息；或更多，无论攻击者可用的密码数量如何，任何密码分析都不会破坏密码。到目前为止，只有一次性PAD（OTP）方法以明确的假设符合此条件。在当前应用程序中需要对加密数据进行操作的同态加密方案的设计才能达到最高的隐私水平。但是，使用OTP的现有对称解决方案有关键管理问题；它们不是线性加密，这意味着它们具有较高的计算复杂性，其中一些不符合所有同构特性。即使攻击者具有强大的计算能力，即使考虑到这些问题，本文也会模拟OTP，并实现对密码分析的最大阻力。提出的基于OTP的方法的第一个主要优势是它仅使用单个预共享密钥。键由两个部分组成，固定数量的位，然后是随机位；每个部分的大小取决于系统的鲁棒性。对所提出的技术的分析表明，它通过使用其他键来加密每个消息来提供完美的隐私。