XiaoMi-AI文件搜索系统
World File Search System模拟Sigmoid函数及其近似导数的设计方法
摘要 — 在本文中,我们建议使用模拟电路实现 S 型函数,该函数将用作多层感知器 (MLP) 网络神经元的激活函数,以及其近似导数。文献中已经提出了几种实现方法,特别是 Lu 等人 (2000) 的实现方法,他们提供了采用 1.2 µ m 技术实现的可配置简单电路。在本文中,我们展示了基于 Lu 等人的 S 型函数电路设计,使用 65 nm 技术以降低能耗和电路面积。该设计基于对电路的深入理论分析,并通过电路级模拟进行验证。本文的主要贡献是修改电路的拓扑结构以满足电路所需的非线性响应以及提取所得电路的直流功耗。索引词——激活函数、模拟 CMOS 电路、近似导数、反向传播、多层感知器、S 型函数。
稳定性和控制导数的确定…… - CORE
图 8.3:横向方向 a = 30° 时计算和测量的响应 T'nne 历史 (a) 侧滑角 (b) 滚动力矩 (c) 偏航力矩 (d) 滚动角 (e) 横向加速度
量子力学中的协变导数,Aharonov–...
其中 σ x 、σ y 、σ z 是作用于自旋的泡利矩阵,g 是旋磁因子。(对于电子,g ≈ 2。)由于磁场 B 是规范不变的,因此方程 (15) 与方程 (14) 一样具有协变性。
相对于连续尺度空间的近似属性,用于高斯导数算子的混合离散
本文基于与归一化采样的高斯核或综合高斯内核的卷积,对高斯衍生物的两种混合离散方法的性质进行了分析。研究这些离散方法的动机是,在相同规模水平上需要多个阶的多个空间衍生物时,与基于更直接的衍生近似值相比,它们基于基于更直接的衍生近似值而具有更高的效率相比,它们基于具有较高的衍生性速率,以示例性衍生性衍生性不能衍生性不能进行。我们根据定量绩效指标来表征这些混合离散方法的特性,同意它们所暗示的空间平滑量,以及它们从量表 - 流动特征探测器的相对一致性以及从自动量表选择中获得的量表的相对一致性,从尺度上的量表与尺度相关的量度相差很大,该尺度的范围与尺度的相差相差,该尺度的尺度是有效的。理论以及不同类型的离散方法之间。在设计和解释以非常精细的水平运行的规模空间算法的实验结果时,提出的结果旨在作为指导。
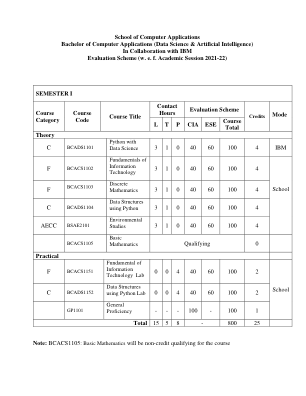
sca-bbdu-bca-ds-and-ai-2021-22.pdf
导数的解释,简单代数和三角函数的导数,和/差的导数,函数的乘积和商,积分:积分作为微分的逆,代数和三角函数的积分,定积分。
航空航天系统 - people@unipi
2.横向平面的静态稳定性主要由风向标导数(即C n b > 0 或 N b > 0 )和二面角导数(即C l b < 0 或 L b < 0 )决定
分数薛定谔方程中双曲双阱势的量子信息熵
摘要:在本研究中,我们研究了双曲双阱势 (HDWP) 的分数阶薛定谔方程 (FSE) 中的位置和动量香农熵,分别表示为 S x 和 S p 。我们在分析中探索了用 k 表示的分数阶导数的各种值。我们的研究结果揭示了有关低位态的位置熵密度 ρ s ( x ) 和动量熵密度 ρ s ( p ) 的局部化特性的有趣行为。具体而言,随着分数阶导数 k 的减小,ρ s ( x ) 变得更加局部化,而 ρ s ( p ) 变得更加非局部化。此外,我们观察到随着导数 k 的减小,位置熵 S x 减小,而动量熵 S p 增加。特别地,这些熵的总和随着分数阶导数 k 的减小而持续增加。值得注意的是,尽管随着 HDWP 深度 u 的增加,位置 Shannon 熵 S x 增加,动量 Shannon 熵 S p 减少,但 Beckner–Bialynicki-Birula–Mycielski (BBM) 不等式关系仍然成立。此外,我们研究了 Fisher 熵及其对 HDWP 深度 u 和分数阶导数 k 的依赖关系。结果表明,Fisher 熵随着 HDWP 深度 u 的增加和分数阶导数 k 的减小而增加。
航空航天系统 - people@unipi
2.横向平面的静态稳定性主要由风向标导数(即C n b > 0 或 N b > 0 )和二面角导数(即C l b < 0 或 L b < 0 )决定
自动微分技术及其在...中的应用
如果函数求值被编码在软件组件中,那么很自然地会问是否可以使用函数求值组件自动计算导数。直到最近,数值求导数的标准方法是使用有限差分,本质上是用 h 来求 (1) 的右侧,h 是一个预先指定的小非零数。这种方法通常会给出一个近似值。近年来,计算机和计算机语言的进步使得开发出一种新方法来获得任何可编程函数的精确导数成为可能。术语自动微分 (AD) [17] 通常适用于从函数求值软件组件生成计算方案(也在软件中实现)的技术,该方案用于计算导数。这些技术已经发展并且仍在发展中,无论是在理论基础方面,还是在其实现的软件工程方面,这一点更为明显。相当成熟的 AD 软件实现出现在 20 世纪 90 年代初 [3],现在该过程有两种“形式”,即反向自动微分 [19] 和正向自动微分 [3]。