XiaoMi-AI文件搜索系统
World File Search Systemun-weyl-ing the clifford层次结构
Gottesman and Chuang(1999)引入的量子组合的传送模型激发了Clif-Ford层次结构的发展。尽管具有量子计算的内在价值,但与该模型密切相关的魔术状态蒸馏的广泛使用强调了理解层次结构的重要性。除了诊断单位的情况外,人们对该等级结构的结构有限有限(Cui等,2017; Rengaswamy等人。2019)。我们通过Weyl(即Pauli)在这些级别上扩展了层次结构的第二和第三层的结构,第一个级别是无处不在的Pauli组。尤其是我们对Pauli Group上标准的操作的支持。自从第三级统一的保利会产生Trace-Lise Hermitian Cli效应以来,我们也表征了他们的Pauli支持。半单位单位在电视模型中节省了Ancilla,我们通过同骨转移探索他们的Pauli支持。最后,我们证明,直到通过clif-ford乘法,每个第三级统一通勤至少都使用一个Pauli矩阵。这可以无力地使用,以表明,直到通过cli的繁殖,每个第三级统一都在保利组的最大交换亚组上进行。另外,可以看出,后者意味着Beigi和Shor(2010)证明的广义半乳房构想。我们讨论了量子误差校正和高空产品设计中的潜在应用。
神经元作为量子参考系的层次结构。
神经元是典型的生物信息处理器。然而,神经信息处理的理论模型,尤其是概念模型,越来越落后于我们对神经元作为电兴奋细胞的不断发展的经验理解。例如,过去二十年的实验工作已经明确证实,树突会经历活动依赖性重塑 [1, 2, 3],特别是树突棘位置、密度和功能的改变 [4],即使在成年人中也是如此。这种个体发生过程在功能上类似于树突结构和位置多样性的进化,因为它们已经适应了一系列功能角色 [5],例如通过突触可塑性实现深度学习 [6, 7]。因此,神经元不是静态结构,而是可以被视为在整个生命周期中不断发育。这一动态过程对神经元级和生物体级功能都有重大影响。例如,在大脑发生剧烈重塑和重建的生物体(如毛毛虫转变为蝴蝶或飞蛾)中,它们学到的一些记忆会保留下来并经受住这一过程 [8]。在其他情况下,记忆可以印刻在从其他组织再生的新大脑上 [9, 10],这凸显了大规模神经结构及其存储信息的可塑性。重塑的这些影响不仅仅是所谓的低等动物的问题,因为再生医学的应用很可能很快就会产生人类患者,他们的部分大脑已被幼稚干细胞的后代所取代,以治疗退行性疾病或脑损伤。
生物多样性获得层次结构
必须在生物多样性收益计划中证明生物多样性增益层次结构在实现10%BNG的方法中如何遵循。如果尚未应用层次结构,则必须提供理由。应用层次结构意味着按以下优先顺序交付BNG:
医疗保健建筑GLN层次结构
GS1 Global的成员 GS1US®是一个非营利的信息标准组织,可通过使用GS1标准(世界上最广泛使用的供应链标准系统)来促进行业协作,以帮助提高供应链的可见性和效率。 25个行业的近300,000家企业依靠GS1 US进行交易伙伴合作,以优化其供应链,驱动成本绩效和收入增长,同时还可以实现监管合规性。 他们通过基于GS1全球唯一编号和标识系统,条形码,电子产品代码(EPC®)的RFID,数据同步和电子信息交换的解决方案实现这些好处。 GS1 US还管理联合国标准产品和服务代码®(UNSPSC®)。GS1US®是一个非营利的信息标准组织,可通过使用GS1标准(世界上最广泛使用的供应链标准系统)来促进行业协作,以帮助提高供应链的可见性和效率。25个行业的近300,000家企业依靠GS1 US进行交易伙伴合作,以优化其供应链,驱动成本绩效和收入增长,同时还可以实现监管合规性。他们通过基于GS1全球唯一编号和标识系统,条形码,电子产品代码(EPC®)的RFID,数据同步和电子信息交换的解决方案实现这些好处。GS1 US还管理联合国标准产品和服务代码®(UNSPSC®)。
层次结构自动组织系统...
由于动态和不可预测的开放世界设置,在Minecraft中导航的复杂环境对多代理系统构成了重大挑战。代理必须与环境互动,并与其他代理人协调其行动以实现共同目标。然而,传统方法通常难以有效地管理代理间的沟通和任务分配,这对于有效的多代理导航至关重要。此外,对代理人了解其目标并成功,全面浏览环境至关重要,处理和集成多模式信息(例如视觉,文本和听觉数据)至关重要。为了解决此问题,我们设计了具有框架来自动化基于LLM的代理以完成导航任务。在我们的方法中,我们设计了一个层次自动组织导航系统,该系统的特征是1)用于多机构组织的层次结构系统,以确保集中式计划和分散的执行; 2)自动组织和内部通信机制,在子任务下进行动态组调整; 3)多模式
使用分析层次结构过程
•在1990年代开发的决策过程,以帮助通过复杂的优先级方案进行工作;在军事,政府,私营部门和学术界中广泛使用。•基于支持决策过程而不是直觉的知识来鼓励决策。•通过一次比较两个标准(即成对比较)来简化过程,以确定哪些对决策目标更重要。•采用以客观,加权标准和替代方案为中心的多层次(分层)结构。
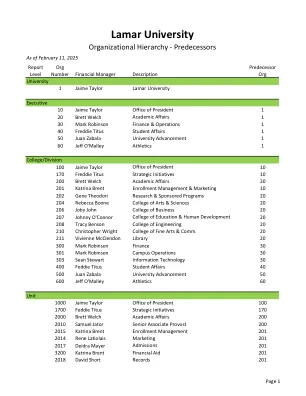
组织层次结构 - 前任(PDF)
前任org 2019 Gabriel Crosby学生成功2016 2016 Samuel Jator认证和评估200 2020 Gene Theodori Research&Sponsed计划202 2040 Rebecca Boone Art&Sciences 204 2060 2060 2060 Joby John Business国家批准中心200 2090布雷特·韦尔奇距离教育2002100克里斯托弗·赖特美术与传播学院210 210 2110 Vivienne McClendon图书馆21111 212 2120 Brett Welch毕业生研究200 2130 TILISA TILISA THIBODEAUX TALH&HONORS&HONORS PROGRAM Facilities 301 3030 Sean Stewart Information Technology 303 3040 Marsha Worthy Human Resources 300 4000 Freddie Titus Student Affairs 400 4100 Freddie Titus Student Activities 400 4200 Shawn Gray Student Facilities 400 4300 Freddie Titus Aux Debt Service 400 4500 Freddie Titus Student Services 400 5000 Juan Zabala University Advancement 500 6000 Jeff O'Malley Athletics 600前任org 2019 Gabriel Crosby学生成功2016 2016 Samuel Jator认证和评估200 2020 Gene Theodori Research&Sponsed计划202 2040 Rebecca Boone Art&Sciences 204 2060 2060 2060 Joby John Business国家批准中心200 2090布雷特·韦尔奇距离教育2002100克里斯托弗·赖特美术与传播学院210 210 2110 Vivienne McClendon图书馆21111 212 2120 Brett Welch毕业生研究200 2130 TILISA TILISA THIBODEAUX TALH&HONORS&HONORS PROGRAM Facilities 301 3030 Sean Stewart Information Technology 303 3040 Marsha Worthy Human Resources 300 4000 Freddie Titus Student Affairs 400 4100 Freddie Titus Student Activities 400 4200 Shawn Gray Student Facilities 400 4300 Freddie Titus Aux Debt Service 400 4500 Freddie Titus Student Services 400 5000 Juan Zabala University Advancement 500 6000 Jeff O'Malley Athletics 600
通过零件式层次结构消息传递
生成的3D部分组装涉及了解零件关系,并预测其6-DOF姿势,用于组装逼真的3D形状。先前的工作通常集中在各个部分的几何形状上,忽略了整个物体的零件。利用两个关键的观察:1)超级部分姿势提供了有关零件姿势的强烈提示,而2)由于较少的超级部分,预测超级零件的姿势更容易,我们提出了一个零件 - 整个层次结构消息传递网络,以实现有效的3D零件组件。我们首先通过在没有任何语义标签的情况下对几何相似部分进行分组,从而引入超级零件。然后,我们采用零件整体的层次编码器,其中超级零件编码器预测基于输入部分的潜在超级零件姿势。随后,我们使用潜在姿势转换点云,将其馈送到零件编码器中,以汇总超级零件信息和有关零件关系的推理以预测所有部分姿势。在培训中,仅需要地面零件姿势。在推断期间,超级零件的预测潜在可增强可解释性。Partnet数据集上的实验结果表明,我们的方法可以部分地达到最新的功能和连接精度,并实现可解释的层次结构组件。代码可在https://github.com/pkudba/3dhpa上找到。
基于测量的量子计算资源的层次结构
摘要对于某些受限制的计算任务,量子力学在任何可能的经典实现方面都提供了可证明的优势。使用了基于测量的量子计算(MBQC)的框架证明了其中几个结果,其中非局部性和更常见的上下文性已被确定为某些量子计算的必要资源。在这里,我们通过在允许的操作和可访问量子的数量上完善其资源需求,从而更详细地考虑MBQC的计算能力。更确切地说,我们确定可以在非自适应MBQC中计算哪些布尔函数,其本地操作包含在Clifford层次结构中的有限级别内。此外,对于限制于某些子理论(例如稳定器MBQC)的非自适应MBQC,我们计算计算给定布尔函数所需的量子数量最少。我们的结果指出了资源的层次结构,这些层次结构更敏锐地描述了MBQC的力量,而不是上下文性与非上下文性的二进制。