XiaoMi-AI文件搜索系统
World File Search System应用数学
lothar-collatz-kolloquium用于应用数学
Zusammenfassung/摘要：在处理随机不等式约束时，机会约束代表了随机优化的主要工具。他们允许人们找到满足不平等约束的最佳决定。最初是在运营研究（有限维度优化）的情况下引入的，其中包括用于水库操作或混合问题的应用，最近在最佳控制方面引起了很多关注，特别是规避风险的PDE受限优化。讨论涉及应用程序（气体传输，最佳调度微型芯片），算法方面（椭圆分布的随机向量的球形 - 辐射分解）以及与最佳控制中机会约束相关的理论结果（最佳条件，解决方案的存在）。kontakt：Caroline Geiersbach Angewandte Mathematik Raum 105，电话。：040 42838-5156电子邮件：caroline.geiersbach@uni-hamburg.de
桥接应用数学和人工智能
机器学习是人工智能的一部分，涉及开发算法，使计算机可以根据数据学习和进行预测。与传统的编程不同，在为每个任务编码特定的说明时，ML算法确定数据中的模式并随着时间的推移提高其性能。此功能对于从自然语言处理和图像识别到自动驾驶汽车和预测分析的应用至关重要。应用数学在此过程中起着至关重要的作用，提供了开发，分析和优化ML算法所需的工具和框架。从线性代数和微积分到概率和优化，数学概念是理解和推进机器学习技术不可或缺的[1]。
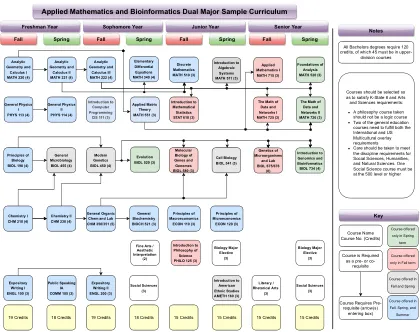
应用数学和生物信息学双重样本课程
哲学课程不应是逻辑课程的两个通识教育课程的两个课程，以满足国际和美国多元文化覆盖要求，以满足社会科学，人文科学和自然科学的学科要求。一个社会科学课程必须在500级或更高的水平上
应用数学中的Cyril Tain医生
•2023年研究与教学的临时立场（ATER）。受试者（级别）：科学计算（数学三年级学生），统计数据（生物学的第三年学生），概率和统计学（信息学二年级学生），基本计算学（基本计算学生（化学中的一年级学生））。鲁恩·诺曼底大学。
应用数学（APMT）2024-2025转移课程表
大调换。职业和教育机会，通过运用统计学，计算科学，金融，经济学和数学的技术知识的人们来实现许多技术和业务的进步。应用数学中的课程在所有这些领域提供了研究，并提供了足够的选修课，以便对任何这些领域进行进一步的深入研究。实际上，该课程中有七个独立的重点领域：精算科学，生物科学，计算科学，密码学，经济学，数学和统计。精算科学重点包括数学金融。一名完成该计划的学生准备使用与技术行业和/或现代金融市场相关的分析和定量工具进入工作。完成生物科学轨道的学生将100％符合医学院的先决条件。对于我们所有应用的数学学位选项，选择适当的选修课，学生就可以在数学，计算机科学，数据科学，经济学，金融，统计学等方面进入定量定向的职业，甚至是研究生课程。有关职业选择的更多信息，请访问careercenter.tamu.edu。转移课程表注释1。入学偏好是向GPA最高且最合适的课程完成的申请人提供的。2。调试申请人被鼓励完成大学核心课程课程，除非指定
用于应用数学和相关学科的模型和算法的本体论
将以下情况作为指导示例：我们想检查某些多孔介质的样本，例如开放式沥青混凝土，并使用微型X射线计算机断层扫描（X-RCT）扫描来检测材料中的微断裂[18]。测量过程可以通过以下意义通过ra trans形对数学建模：当X射线在线上通过对象行进时，该线路上的材料将使它减弱。这种衰减取决于我们要重建材料的密度。在数学上，在检测器中测得的信号现在可以表示为ra换变换，即所谓的X射线函数的X射线变换。因此，要重建断裂图像，必须将用于X射线变换反转的算法应用于观察到的数据。除其他外，算法的选择取决于所测量的数据和模型的属性，例如所使用的坐标系。这些元数据通常不会系统地存储，从而违反了公平原则[28]，因为无法保证可重复使用性。因此，有兴趣应用X-RCT（可能在考古学或生物医学等其他研究领域）的研究人员不能简单地重复使用，但可能必须重新验证文献搜索算法，软件实现和参数。由于其来自工程的起源，来自不同领域的数据与基本的一般数学概念没有链接。因此，尽管基本的数学模型可能完全相同，但应用程序之间的协同作用并未利用。1应该被捡起。创建知识图（kg），包括模型，算法，相关文献和进一步的元数据，这是本文的范围。通常，在典型的建模仿真 - 优化（MSO）工作流程中产生的问题如图所示。这些包括模型的实验，解决方案算法的可用性，输入或观察数据或模型有效性。通常，回答这些问题需要大量的努力，如果所需的信息可访问并删除 -
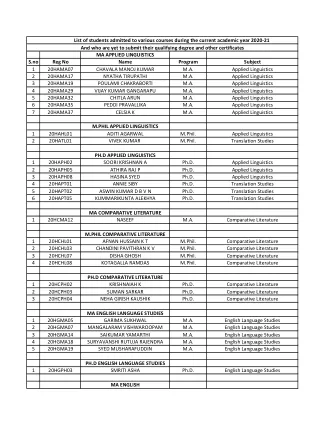
应用语言学文学硕士 S.no 注册号 姓名 课程 科目 1 20HAMA07 CHAVALA MANOJ KUMAR 应用语言学文学硕士 2 20HAMA17 NYATHA TIRUPATHI 应用语言学文学硕士
MSC 数学 1 20MMMM05 RAMESH BABU M 理科硕士 数学/应用数学 2 20MMMM09 KAUSTUVA GHOSH 理科硕士 数学/应用数学 3 20MMMM10 JOYDIP MONDAL 理科硕士 数学/应用数学 4 20MMMM14 SUDIP MANNA 理科硕士 数学/应用数学 5 20MMMM20 SANDIPAN DAS 理科硕士 数学/应用数学 6 20MMMM23 RIYA MANDAL 理科硕士 数学/应用数学 7 20MMMM26 RASMITA BEHERA 理科硕士 数学/应用数学 8 20MMMM28 K SUVARNA KUMARI 理科硕士数学/应用数学 9 20MMMM30 MANYA RAJ 理学硕士 数学/应用数学 10 20MMMM31 KUNDAN YADAV 理学硕士 数学/应用数学 11 20MMMM32 NAUMAN ANSARY 理学硕士 数学/应用数学 12 20MMMM33 SAFURUDDIN MONDAL 理学硕士 数学/应用数学 13 20MMMM36 PAWAN KUMAR SAW 理学硕士 数学/应用数学 14 20MMMM38 ARKA GHOSH 理学硕士 数学/应用数学 15 20MMMM43 AVIRAL SRIVASTAVA 理学硕士 数学/应用数学 16 20MMMM44 SASWATA GHOSH 理学硕士数学/应用数学 17 20MMMM46 RIJU PATRA 理学硕士 数学/应用数学 18 20MMMM50 KARIMAJJI KESAVARAO 理学硕士 数学/应用数学 19 20MMMM57 ANWESHA SAMANTA 理学硕士 数学/应用数学
