XiaoMi-AI文件搜索系统
World File Search System微积分
11:00 MATH101微积分I星期六18.01
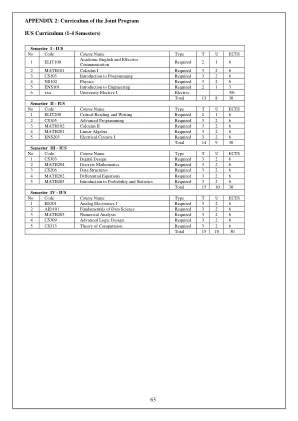
2 MATH101 Calculus I Required 3 2 6 3 CS103 Introduction to Programming Required 3 2 6 4 NS102 Physics Required 3 2 6 5 ENS101 Introduction to Engineering Required 2 1 3 6 xxx University Elective I Elective 3/6 Total 13 8 30 Semester II - IUS No Code Course Name Type T U ECTS 1 ELIT200 Critical Reading and Writing Required 2 1 6 2 CS105 Advanced Programming Required 3 2 6 3 MATH102 Calculus II Required 3 2 6 4 MATH201 Linear Algebra Required 3 2 6 5 ENS203 Electrical Circuits I Required 3 2 6 Total 14 9 30 Semester III - IUS No Code Course Name Type T U ECTS 1 CS303 Digital Design Required 3 2 6 2 MATH204 Discrete Mathematics Required 3 2 6 3 CS206 Data Structures Required 3 2 6 4 MATH202 Differential Equations Required 3 2 6 5 MATH203 Introduction to Probability and Statistics Required 3 2 6 Total 15 10 30学期IV -IUS无代码课程名称类型T U ECTS 1 EE201模拟电子I需要3 2 6 2 AID101数据科学的基本原理需要3 2 6 3 MATH205数值分析需要3 2 6 4 CS309先进的逻辑设计需要3 2 6 5 CS313计算的理论需要3 2 6总计15 10 30 30 30 30 30
教学大纲 - 机械工程 / 学士学位 / 机械工程 / 机械工程 - 2024 学时：1 CM310 - 预科微积分 PD：60 教学大纲
巴拉那联邦大学 - CNPJ 75.095.679/0001-49 Cel。 Francisco H. dos Santos - 库里蒂巴 - 巴拉那州 - 巴西邮政编码 81531-980 - 电话：(41) 3361-3131 - 电子邮件：ccem@ufpr.br https://siga.ufpr.br/siga/visitante/autenticacao.jsp - 验证码：BprWjqV6k
MATH1020-微积分和线性代数II-单位指南
单元描述Math1010中引入的线性代数和微积分的基础进一步探索和扩展。用代数涵盖的主题包括：反矩阵，决定因素，矢量空间和子空间，特征值以及特征向量以及线性变换。在微积分中，主题包括：限制，连续性和衍生物，数值集成，多项式，序列和序列和微分方程的进一步发展。另外，引入了两个或多个变量的复数和计算。学生在整个课程中都利用数学软件来支持和加强解决各种理论和实际问题的问题。
数学 311 – 微积分 III – 教学大纲
另一个。• 找到空间中直线的参数和对称方程。• 找到空间中两个物体之间的距离。• 识别空间中的表面。• 确定矢量值函数的极限、连续性、导数和积分。• 使用向量解决涉及速度、力和功的应用问题。• 确定矢量值函数的曲率。• 找到矢量值函数的单位切向量、法向量和副法向量
ZX 微积分中的 QECC 的规范形式和等价类
需要量子纠错码 (QECC) 来对抗影响量子过程的固有噪声。使用 ZX 演算，我们将 QECC 表示为一种称为 ZX 图的形式，该图由节点和边组成。在本文中，我们给出了环面码和某些曲面码的 ZX 图的规范形式。我们通过使用双代数规则（该规则删除了多余的内部节点并通过 Quantomatic 实现）和边局部补充规则（该规则交换两个节点的颜色）重写这些形式来推导这些形式。接下来，我们将等价类制成表格，包括它们的大小和二分形式是否存在等属性，以及 QECC 的一般 ZX 图。这项工作扩展了之前在 ZX 图表示中探索 QECC 的规范形式的工作。
mth 137：大学微积分1B
第二个衍生物 - 使用衍生物来绘制函数图 - 陈述平均值定理并将其应用于计算 - 应用L'Hospital的规则来计算功能限制 - 使用衍生物解决优化问题 - 使用衍生物来解决涉及直线运动的实际问题。
材料科学与工程 – 预微积分
数学 AP 微积分 AB 成绩为 3：MATH 1710 AP 微积分 BC 成绩为 3：MATH 1710、1720 AP 微积分 AB BC 考试成绩为 3：MATH 1710 IB 数学 - 微积分：MATH 1710 CLEP 大学代数：MATH 1100 CLEP 预科微积分：MATH 1650 CLEP 微积分：MATH 1710 社区学院 MATH 1314：MATH 1100 社区学院 MATH 1414：MATH 1100 社区学院 MATH 1442：MATH 1680 社区学院 MATH 2312：MATH 1650 社区学院 MATH 2412：MATH 1650 社区学院 MATH 2313：MATH 1710 社区学院 MATH 2314：MATH 1720 社区学院 MATH 2315：MATH 2730 社区学院 MATH 2320：MATH 3410 的替代课程 社区学院 MATH 2413：MATH 1710 社区学院 MATH 2414：MATH 1720 社区学院 MATH 2415：MATH 2730 社区学院 MATH 2420：MATH 3410 的替代课程
面向学生和专业人士的基础 ZX 微积分
ZX 演算 [7, 8, 9] 早在 2007 年就已经出现，但只是在过去几年才开始广泛应用，尤其是随着量子产业的兴起，这带来了新的科学和技术挑战 [12]。它在编译 [17, 27]、电路优化 [20, 28]、纠错 [18, 22]、量子自然语言处理 [6]、QML [35, 34]，以及围绕光子量子计算的诸多问题 [19, 29]。它最近声名鹊起的另一个原因是有了《量子过程图解》[14] 一书，该书在介绍 ZX 演算时没有参考范畴论，而范畴论以前对很多人来说是个障碍。更重要的是，最近还有一本书《量子图解》[11]，它不需要任何数学前提条件。因此，本书还将 ZX-calculus 确立为一种教育工具，它可以为使量子更具包容性做出重要贡献，同时提供一个全新的视角。
微积分导论 - 哈佛数学系
0.1。本课程是微积分的入门课程，于 2011-2014 和 2020-2021 年在哈佛大学教授。虽然不需要之前接触过微积分，但需要具备几何和代数等基本的微积分预备技能。即使你以前学过一些微积分，像这样的大学单变量微积分课程也会让你对这个主题有更深入、更概念性的理解。它让你看到数学理论的美丽和优雅，并欣赏它的应用。虽然概念和应用都很重要，但技能的掌握也是关键。尤其是在一个新领域的第一步，你必须专注于技能。幸运的是，程序比洞察力更容易学习和教授，洞察力需要更多的时间，因为它需要经验和连接点的能力，看到相似之处、模式和提出问题的能力。
CHAP E4120 Ben O'Shaughnessy 教授 3 分 先决条件：热力学、初等概率论和统计过程、微积分。
课程背景 统计力学解释热力学并能够根据分子计算材料特性。 当热力学刚刚发展起来时，人们并不知道物质是由分子组成的！因此，热力学定律的起源也是未知的。 (1) 热力学并没有告诉我们定义材料的状态函数是什么，E(S,V,N) 还是 F(T,V,N) 还是 G(T,P,N) 还是 H(S,P,N) 等。这些函数是热力学定律的输入数据，必须针对每种材料进行测量。我们不能使用热力学来计算这些函数。 (2) 热力学也没有基本的微观基础——它基于经验假设。第二定律和熵特性的存在基于经验假设，通常是“热量不会自发地从一个物体流向另一个更热的物体。”为什么这是真的？热力学无法回答这个问题。统计力学给出了答案，而且非常简单。1874 年，奥地利物理学家路德维希·玻尔兹曼 (Ludwig Boltzmann) 提出了著名的熵假说，将宏观（热力学）世界与微观世界联系起来：𝑆= 𝑘 𝐵 𝑙𝑛 Γ 。其中 Γ 是可能状态的数量（与约束条件一致），𝑘 𝐵 是玻尔兹曼常数。因此，我们所要做的就是计算分子可能处于多少种状态，这就可以得出熵（从中可以得到所有其他热力学函数，如 F、G、H、Ω ）。因此，如果分子是已知的（因此它们的相互作用也是已知的，等等），那么就可以得到所有的热力学函数，并且可以预测所有材料在不同过程中的性质和行为。第二定律 ΔS 宇宙 > 0 是玻尔兹曼假设的必然结果，也是合乎逻辑的。很明显，这一定律完全是材料分子性质的结果。它解释了时间之箭，这是牛顿和量子力学基本自然定律中缺失的，这些定律表现出 t→-t 不变性（想象一下台球桌上两个球的碰撞——如果你倒着播放这部电影，你不会知道，因为牛顿定律仍然适用）。基于分子的工程设计。因此，统计力学提供了微观和宏观、分子世界和材料世界之间的联系。因此，它为现代分子工程时代打开了大门，这是化学工程的现在和未来的核心。统计力学使我们能够设计分子（甚至构建全新的分子，如聚合物），这些分子将构成具有所需特性的新材料，构建利用分子应用于传感和其他新技术的纳米级设备，或了解活细胞中的分子机制，从而指导疾病的治疗和预防。统计分析的计算技术。当然，统计力学是关于统计学。它是统计分析的科学，其概念和工具旨在分析和理解涉及大量变量的复杂随机过程。当今用于解决涉及大量变量的统计问题的计算方法库主要诞生于统计力学领域。如今，这些方法不仅用于分子系统的研究，还用于从大脑神经回路到人工智能再到数据科学的各种应用。