XiaoMi-AI文件搜索系统
World File Search System本科数学评估实践
11.助教和兼职教师改进教学的关键,助教和兼职教师委员会,Bettye Anne Case,编辑。13.重塑大学数学,数学本科课程委员会,Lynn A. Steen,编辑。14.数学写作,Donald E. Knuth、Tracy Larrabee 和 Paul M. Roberts 著。16.用写作来教数学,Andrew Sterrett,编辑。17.启动微积分泵:创新和资源,微积分改革委员会和前两年,数学本科课程委员会的一个小组委员会,Thomas W. Tucker,编辑。18.数学本科研究模型,Lester Senechal,编辑。19.数学教学和学习中的可视化,数学教育计算机委员会,Steve Cunningham 和 Walter S. Zimmermann,编辑。20.微积分教学的实验室方法,L. Carl Leinbach 等人。,编辑。21.《当代统计学观点》,David C. Hoaglin 和 David S. Moore 编辑。22.《听从变革的呼声:课程行动建议》,Lynn A. Steen 编辑。24.《本科数学教育中的符号计算》,Zaven A. Karian 编辑。25.《函数概念:认识论和教学法的方面》,Guershon Harel 和 Ed Dubinsky 编辑。26.《二十一世纪统计学》,Florence 和 Sheldon Gordon 编辑。27.微积分资源集,第 1 卷:通过发现学习:微积分实验手册,Anita E. Solow,编辑。28.微积分资源集,第 2 卷:新世纪微积分问题,Robert Fraga,编辑。29.微积分资源集,第 3 卷:微积分的应用,Philip Straffin,编辑。30.微积分资源集,第 4 卷:学生调查问题,Michael B. Jackson 和 John R. Ramsay,编辑。31.微积分资源集,第 5 卷:微积分阅读材料,Underwood Dudley,编辑。32.人文数学论文集,Alvin White,编辑。33.本科数学学习研究问题:初步分析和结果,James J. Kaput 和 Ed Dubinsky,编辑。34.在 Eves 的圈子里,Joby Milo Anthony,编辑。35.你是教授,下一步该怎么做?大学教师准备的想法和资源,大学教学准备委员会,Bettye Anne Case,编辑。36.为新微积分做准备:会议论文集,Anita E. Solow,编辑。37.大学数学合作学习实用指南,Nancy L. Hagelgans、Barbara E. Reynolds,SDS、Keith Schwingendorf、Draga Vidakovic、Ed Dubinsky、Mazen Shahin、G. Joseph Wimbish,Jr。38.有效的模型:有效本科数学课程的案例研究,Alan C. Tucker,编辑。39.微积分:变化的动态,CUPM 微积分改革和头两年小组委员会,A. Wayne Roberts,编辑。
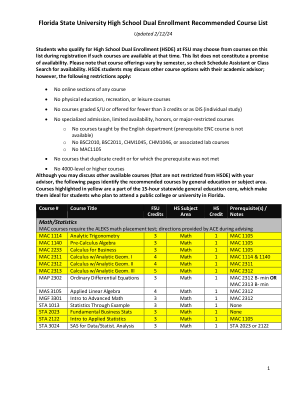
佛罗里达州立大学高中双学分推荐课程列表
先决条件/注意事项 数学/统计学 MAC 课程需要 ALEKS 数学分班考试;ACE 在指导期间提供指导 MAC 1114 解析三角学 3 数学 1 MAC 1105 MAC 1140 预备微积分代数 3 数学 1 MAC 1105 MAC 2233 商务微积分 3 数学 1 MAC 1105 MAC 2311 微积分与解析几何 I 4 数学 1 MAC 1114 和 1140 MAC 2312 微积分与解析几何 II 4 数学 1 MAC 2311 MAC 2313 微积分与解析几何III 5 数学 1 MAC 2312 MAP 2302 常微分方程 3 数学 1 MAC 2312 B- min 或 MAC 2313 B- min MAS 3105 应用线性代数 4 数学 1 MAC 2312 MGF 3301 高等数学入门 3 数学 1 MAC 2312 STA 1013 实例统计 3 数学 1 无 STA 2023 基础商业统计 3 数学 1 无 STA 2122 应用统计学入门 3 数学 1 MAC 1105 STA 3024 数据/统计分析 SAS 3 数学 1 STA 2023 或 2122
B.Sci. (数据科学与人工智能)课程适用于 2018 年或以后入学的学生
MH1802 科学微积分 本课程旨在让学生掌握 数学知识和分析技能,使他们能够应用微积分技术(以及他们现有的数学技能)来解决适用的科学问题; 数学阅读技能,使他们能够阅读和理解基础和流行科学和工程文献中的相关数学内容;以及 数学交流技能,使他们能够有效和严格地向数学家、科学家和工程师介绍他们的数学思想。内容基础 (BAS) 数字类型;函数和图形;常用函数及其图形;重要的代数、三角、对数和指数恒等式;基本复数。微积分 (DIF) 极限;微分;微分技术;微分的应用;基本偏导数。积分 (INT) 积分;积分技术;对数、指数和反三角函数的微积分;积分的应用;微分方程 (DE) 基础;一阶常微分方程;二阶常微分方程;级数、序列和微分方程。MH1812 离散数学 学习目标 本课程介绍数学和计算机科学中常用的离散数学基本概念。内容 - 计数、排列和组合、二项式定理 - 递归关系 - 图、路径和电路、同构 - 树、生成树 - 图算法(例如最短路径、最大流)及其计算复杂度、大 O 符号 MH2100 微积分 III 学习目标 这是微积分系列中的最后一门课程。本课程介绍多变量微积分。内容 参数方程、极坐标。向量值函数、向量值函数微积分、立体解析几何。多变量函数、极限、连续性、偏导数、可微分性和全微分、链式法则、隐函数定理。方向导数、梯度、拉格朗日乘数。二重积分、表面面积、三重积分。线积分、格林定理、曲面积分、高斯散度定理、斯托克斯定理。
学士学位:信息工程 学习计划
微积分 1 12 计算机科学基础 12 英语语言 B2 3 线性代数 12 物理 1 12 数字系统 9 数据结构与算法 9 微积分 2 9 物理 2 9 概率论 9 信号与系统 9 电路 6 机器学习简介 6 电子学 9 电信 9 控制系统 9 期末考试 3
课程大纲Econ 481发展的微观经济学
•ECON 303是本课程的先决条件。•微积分:虽然不是正式的先决条件,但有时我们会使用微积分大致相当于大多数中级微观经济理论课程中使用的微积分。我会假设您对基础知识感到满意,并且愿意在课堂上拿起其余的东西。•统计:我将假设一些统计背景(平均值,方差,平均值比较,概括间隔,假设检验)。计量经济学不是先决条件,尽管它将是有用的背景知识。我们将介绍相关的计量经济学工具,以参与课堂上的经验发展微观经济学研究。
理学院 (FS)
基础课程必修课程(146 学分)线性代数:矩阵计算(2 学分)。算法(6 学分)。矢量微积分(6 学分)。英语水平 A(4 学分)。微积分 I(4 学分)、生物物理学(4 学分)、概率计算(4 学分)、数值微积分:MATLAB(2 学分)、普通化学 I(6 学分)。微积分 II(2 学分)。电磁学(4 学分)。基础电子学(6 学分)。静电学和电动力学(4 学分)。函数 I(4 学分)。电子学概论(4 学分)。物理仪器(4 学分)。医学物理学概论(4 学分)。日常生活中的 USJ 价值观(2 学分)。符号计算软件:Maple(2 学分)。静磁学(4 学分)。物理学家的数学(6 学分)。分析力学(4 学分)。经典力学(4 学分)。高级经典力学(2 学分)。流体力学(4 学分)。量子力学(4 学分)。物理学家的数学方法(6 学分)。波和波动光学(6 学分)。物质物理学(6 学分)。现代物理学(6 学分)。统计物理学(4 学分)。Python(4 学分)。狭义相对论(4 学分)。热力学(4 学分)。科学交流技巧(4 学分)。
印度技术学院Indore High ... -CSE/IITI
研讨会数学的简要说明是人工智能(AI)和机器学习(ML)不可或缺的一部分,为算法开发和优化提供了基础框架。来自微积分,线性代数,概率理论和统计的概念是许多AI和ML算法的基础。优化技术(例如梯度下降)在很大程度上依赖于微积分,而概率理论对于理解模型中的不确定性至关重要。数据表示通常涉及矩阵,向量和张量,需要对数学概念有很强的掌握。复杂性分析,包括了解计算效率,从离散的数学和算法分析中获取。诸如降低维度降低和信号处理之类的技术大量利用了数学原理。神经网络是现代AI的中心,深深植根于微积分,线性代数和概率理论。此外,数学对于