XiaoMi-AI文件搜索系统
World File Search System闭合曲线中同源性检测的恒定时间量子算法
给定一个闭二维流形或曲面上的大小为 L 的环或更一般的 1-循环 r(用三角网格表示),计算拓扑学中的一个问题是它是否与零同源。我们在量子环境中构建和解决这个问题。给定一个可以用来查询闭曲线上边的包含情况的 oracle,我们设计了一个用于这种同源性检测的量子算法,相对于环 r 上边的大小或边数,其运行时间为常数,只需要使用一次 oracle。相比之下,经典算法需要使用 Ω( L ) oracle,然后进行线性时间处理,并且可以通过使用并行算法将其改进为对数时间。我们的量子算法可以扩展以检查两个闭环是否属于同一个同源类。此外,它可以应用于同伦检测中的一个特定问题,即检查闭二维流形上的两条曲线是否不是同伦等价的。
型号KBF-S Eco 400 |恒定气候室,具有环保的热电冷却
01凝结可能发生在访问端口周围的区域。可以将访问端口放置在自定义位置以获得额外费用。使用此选项时未授予02 UL标记。03传感器校准是在认可的校准实验室中进行的。04校准是根据粘合剂工厂标准执行的。05报价的价格不包括旅行费用。请参阅有关您所在地区的旅行费用的活页夹服务章节。引用在瑞士执行的服务价格的价格不包括国家规格的附加费(可根据要求提供)。
用于使用模糊逻辑控制器的SECA电动汽车电池充电的恒定电流的方法 - 恒定电压(CC - CV)
摘要。电动汽车是克服化石燃料和环境影响的消耗的解决方案。电动汽车是一种使用电池作为主要能源的电动汽车。充电时,电池容易容易充电,因此需要一个充电系统来保持电池性能以避免电池损坏。在这项研究中,研究人员使用恒定电流 - 恒定电压(CC -CV)的方法测试了SECA电动汽车,该方法在初始阶段应用恒定电流和恒定电压,直到电池充满电。电池类型是具有12V,30AH容量的铅酸电池。该电池充电系统的分析已由模糊逻辑控制器(FLC)证明是基于其规则基础的当前和电压控制器,以提高性能改善充电系统。通过该系统充电电池有望通过在充电过程中避免电池充电来维持电池寿命。
非恒定曲率空间中量子非线性振子的香农信息熵
所谓的达布 III 振子是定义在具有非常量负曲率的径向对称空间上的精确可解的 N 维非线性振子。该振子可以解释为通常的 N 维谐振子的平滑(超)可积变形,其非负参数 λ 与底层空间的曲率直接相关。本文详细研究了达布 III 振子的量子版本的香农信息熵,并分析了熵和曲率之间的相互作用。具体而言,在 N 维情况下可以找到位置空间中香农熵的解析结果,并且在曲率 λ → 0 的极限下可以恢复 N 维谐振子量子态的已知结果。然而,达布 III 波函数的傅里叶变换无法以精确形式计算,从而阻碍了对动量空间中信息熵的解析研究。尽管如此,我们已经在一维和三维情况下对后者进行了数值计算,并且我们发现通过增加负曲率的绝对值(通过更大的 λ 参数),位置空间中的信息熵会增加,而在动量空间中的信息熵会变小。这个结果确实与这个量子非线性振荡器的波函数的扩散特性一致,这在图中得到了明确展示。位置和动量空间中的熵之和也根据曲率进行了分析:对于所有激发态,这种总熵都会随着 λ 的减小而减小,但对于基态,当 λ 消失时,总熵最小,相应的不确定性关系始终得到满足。© 2022 作者。由 Elsevier BV 出版这是一篇根据 CC BY-NC-ND 许可协议开放获取的文章(http://creativecommons.org/licenses/by-nc-nd/4.0/)。
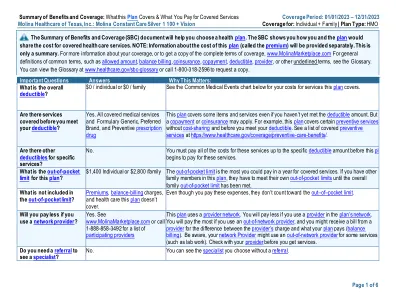
molina恒定护理银1 100 +视觉
福利和承保范围(SBC)文件摘要将帮助您选择健康计划。SBC向您展示了您和计划将如何分享涵盖医疗服务的费用。注意:将单独提供有关此计划成本(称为保费)的信息。这只是一个摘要。有关您的覆盖范围的更多信息,或获取覆盖范围的完整条款的副本,www.molinamarketplace.com,有关通用条款的一般定义,例如允许金额,余额计费,共同账单,共同保险,共同款项,可扣除,提供者,提供者或其他下划线条款,请参见Glosossary。您可以在www.healthcare.gov/sbc-glossary上查看词汇表,或致电1-800-318-2596请求副本。
缺口、名义应力、疲劳强度折减系数和恒定/可变振幅多轴疲劳载荷
机械组件和结构的组成结构元件具有复杂的几何形状,导致局部应力/应变集中现象。这些带缺口的结构部件经常受到随时间变化的载荷,这可能导致疲劳裂纹的产生和扩展。在非常特殊的情况下,使用中的载荷路径包括恒幅 (CA) 疲劳循环。然而,在大多数实际情况下,结构部件受到变幅 (VA) 载荷谱的影响。除此之外,疲劳设计问题进一步复杂化,因为一般来说,实际使用中的载荷历史本质上是多轴的。就受到 CA 多轴疲劳载荷的无缺口金属材料而言,对现有技术的检查表明,使用各种设计标准可以达到良好的精度水平 [1] 。然而,尽管设计可靠性如此令人鼓舞,但显然还需要做更多的工作,以便更好地将材料微观结构的影响纳入疲劳设计过程 [2] 。在此背景下,关键问题是具有不同延展性的材料对施加载荷历史的非比例性程度表现出不同的敏感性 [3] 。虽然已经进行了大量工作来研究普通金属材料的多轴疲劳行为,但迄今为止,国际科学界尚未对多轴疲劳行为进行深入研究。
替代的持续弹性持续多么恒定?清洁和肮脏能量之间的内源性∗
在大多数经济体中,从化石燃料到低碳可再生能源的过渡在阻止变暖进展的政策愿景中起着核心作用(IPCC,2018年)。作为控制过渡过程的关键参数,已证明清洁和肮脏能量之间的替代性程度强烈影响可持续增长和气候政策最佳设计的预测。例如,Acemoglu等。(2012)表明,当干净和肮脏的输入是较弱的替代品或补充时,要避免环境灾难并改用清洁生产,必须使用永久性的碳税,而当两个输入是强大的替代品时,则需要较低和临时的碳税税。进一步,Golosov等。(2014)从其校准模型中注意到,不同燃料之间的高度可替代性诱导了下一个世纪中叶的温度下降,而较低的替代性也涉及即使有最佳政策,温度也持续升高。尽管其重要性,但大多数宏观经济模型以及可计算的一般平衡模型,它们在很长一段时间内产生预测(超过2100)总是会假设清洁和脏输入之间的替代弹性恒定且外源性的弹性。然而,清洁能量的日益增长表明,随着时间的流逝,这种替代性可能会有所改善。为了说明,图1显示了在经济中的清洁能源的渗透,其相对价格在过去三十年中在法国,这是世界第七大经济体。21这些观察结果也与世界各地的新兴政策计划一致,这些计划导致了使用清洁能源的必要技术和基础设施的大量扩展(IEA,2020年)。
利用守恒定律进行信息加扰 - NSF-PAR
量子信息的离域化或扰乱已成为理解孤立量子多体系统中热化的核心要素。最近,通过将不可积系统建模为周期驱动系统,缺乏汉密尔顿图像,而真实的汉密尔顿动力学由于计算限制通常限于小系统规模,在分析上取得了重大进展。在本文中,我们从信息论的角度研究守恒定律(包括能量守恒定律)在热化过程中的作用来解决这个问题。对于一般的不可积模型,我们使用平衡近似来表明,即使系统节省能量,最大量的信息在后期也会被扰乱(以时间演化算子的三部分互信息来衡量)。相反,我们阐明了当系统具有导致光谱退化的额外对称性时,扰乱的信息量必须减少。这一普遍理论在全息共形场论 (CFT) 和 Sachdev-Ye-Kitaev (SYK) 模型的案例研究中得到了体现。由于 1 + 1D CFT 中具有较大的 Virasoro 对称性,我们认为,在某种意义上,这些全息理论并不是最大程度混沌的,这可以通过第二个 Rényi 三分互信息的不饱和明确看出。在 SYK 模型中,粒子空穴和 U ( 1 ) 对称性的作用较弱,因为简并只有两重,我们在大 N 和小 N 时都明确证实了这一点。我们根据局部算子的增长重新解释了算子纠缠,将我们的结果与非时间序相关器所描述的信息扰乱联系起来,从海森堡的角度确定了抑制扰乱的机制。
利用守恒定律进行信息加扰
量子信息的离域化或扰乱已成为理解孤立量子多体系统中热化的核心要素。最近,通过将不可积系统建模为周期驱动系统,缺乏汉密尔顿图像,而真实的汉密尔顿动力学由于计算限制通常仅限于小系统规模,在分析上取得了重大进展。在本文中,我们从信息论的角度研究守恒定律(包括能量守恒定律)在热化过程中的作用来解决这个问题。对于一般的不可积模型,我们使用平衡近似来表明,即使系统节省能量,最大量的信息在后期也会被扰乱(以时间演化算子的三部分互信息来衡量)。相反,我们阐明了当系统具有导致光谱退化的额外对称性时,扰乱的信息量必须减少。这一普遍理论在全息共形场论 (CFT) 和 Sachdev-Ye-Kitaev (SYK) 模型的案例研究中得到了体现。由于 1 + 1D CFT 中具有较大的 Virasoro 对称性,我们认为,在某种意义上,这些全息理论并不是最大程度混沌的,这可以通过第二个 Rényi 三分互信息的不饱和明确看出。在 SYK 模型中,粒子空穴和 U ( 1 ) 对称性的作用较弱,因为简并只有两重,我们在大 N 和小 N 时都明确证实了这一点。我们根据局部算子的增长重新解释了算子纠缠,将我们的结果与非时间序相关器所描述的信息扰乱联系起来,从海森堡的角度确定了抑制扰乱的机制。
b“摘要。我们考虑u t d d r ..u/ r n .u //的方程,其中n是整个空间中newtonian的潜力(laplacian倒数),整个空间r d,.u/是流动性。对于线性流动性,.u/ d u,方程式和某些范围,是针对超级或超级脉动的范围,以实现超级或超级脉络性的范围。具有紧凑空间支撑的特性的弱解决方案,特别是在空间中具有恒定强度的圆盘涡流的特殊解决方案在球中支撑的球中支撑的圆盘涡流,如c 2 t 1 = d的及时散布,因此在本文中显示了不连续的领先者,我们提出了sublinearearearial obyility .u/ d u \ xcb \ xc \ xc的模型。证明非阴性的解决方案在各处恢复了阳性,并且在无穷大的情况下,尤其是以上的脂肪尾巴。 \ xcb \ x9b / /。我们将分析限制在径向溶液中,并通过特征方法构建解决方案。我们介绍了质量功能,该质量函数解决了汉堡方程的异常变化,并在分析中起着重要作用。我们从粘度解决方案的意义上表现出良好的性质。我们还构建了数值有限差分convengen
b“摘要。我们考虑了u t d r ..u/ r n .u //的形式的方程式,其中n是整个空间r d和.u/是纽顿电位(laplacian的倒数),并且.u/是移动性。对于线性迁移率,.U/ D U,已提出方程和一些变化作为超导性或超流体的模型。在这种情况下,该理论会导致具有紧凑空间支持的特性的有界弱解的唯一性,特别是在空间强度u d c 1 t 1中具有恒定强度的圆盘涡流的特殊溶液在球中支撑的恒定强度的涡流涡流,在c 2 t 1 = d之类的时间内传播,因此显示出不连续的前面前面的前线。在本文中,我们提出了具有sublinear Mobility .u/ d u \ xcb \ x9b的模型,并使用0 <\ xcb \ x9b <1提出,并证明非负溶液到处恢复了积极性,并且在无限范围内显示出脂肪尾巴。该模型以许多方式作为上一个模型的正规化。尤其是,我们发现上一个涡流的等效物是一种明确的自相似解,如u d o.t 1 = \ xcb \ x9b /带有尺寸u d o的空间尾巴的时间。我们将分析限制为径向溶液,并通过特征方法构建解决方案。我们介绍了质量函数,该质量函数解决了汉堡方程的异常变化,并在分析中起着重要作用。我们从粘度解决方案的意义上表现出良好的性质。我们还构建了数值有限差分收敛方案。”