XiaoMi-AI文件搜索系统
World File Search System方程系统
搜索定义QUBO问题AES Sbox的有效方程系统
摘要解决QUBO问题的时间复杂性主要取决于概率中逻辑变量的数量。本文主要集中于找到一个方程系统，该方程式唯一地定义了AES密码的Sbox，并允许我们在QUBO形式中获得代数攻击AES密码的QUBO形式中最小的已知优化问题。为了有效地执行该任务，已经提出了一种使用线性反馈移位寄存器搜索有效方程式的新方法。使用已确定的效率系统将AES密码转换为QUBO问题。与我们先前的结果相比，此方法使我们能够将AES-128的目标Qubo问题减少近500个逻辑变量，并允许我们使用量子退火速度快四倍地执行代数攻击。
计算机科学（CSCI）
CSCI U421算法的设计和分析3个学时概念和算法设计的基本策略；计算时间和内存要求的分析；计算复杂性理论（NP-HARD和NP完整）；图形操纵算法（连接的组件，最小跨越树，旅行推销员，图表中的周期以及图形的着色）；搜索算法（第一个深度，第一个，最佳和alpha-beta minimax）；和计算算法（矩阵乘法，线性方程系统，表达评估和排序）。先决条件：CSCI U321中的C等级或更高；或讲师的同意。
来自安全多方计算的Quantum签名
我们使用“头号MPC”范式提供了几种新的签名模式。他们中的大多数都具有质量后艺术状态的现有模式竞争。它们产生的签名尺寸在5到20公斤（对于128位的安全级别）之间，并且钥匙很小（小于200个字节）。这些模式的安全性的分支问题非常多样化。某些图是基于误差代码理论的安全假设，例如在困难中解决综合征解码问题的问题。其他图依赖于二合一的二次方程系统，子组件总和或采矿问题的问题。
使用 ALTAIR SIMSOLID™ 技术概述
20 世纪初发明的用于近似解决边界值问题的 Ritz-Galerkin 方法假设近似解的函数是定义在整个相关域上的解析函数。在实际应用中，这些函数要么是三角函数，要么是无限平滑的多项式，即它们有无数个导数。此类函数有两个主要问题。首先，很难或不可能构建先验满足任意域边界上基本边界条件的函数（在结构分析中，这些条件表现为位移约束）。其次，基于此类函数构建的方程系统病态且数值不稳定，无法以足够高的精度解决实际问题。
Altair SimSolid 白皮书 - 技术概述_2019 年 2 月
20 世纪初发明的用于近似解决边界值问题的 Ritz-Galerkin 方法假设近似解的函数是定义在整个相关域上的解析函数。在实际应用中，这些函数要么是三角函数，要么是无限平滑的多项式，即它们有无数个导数。此类函数有两个主要问题。首先，很难或不可能构建先验满足任意域边界上基本边界条件的函数（在结构分析中，这些条件表现为位移约束）。其次，基于此类函数构建的方程系统病态且数值不稳定，无法以足够高的精度解决实际问题。
基础工程科学系
等级，正常形式，线性方程系统，线性独立和依赖的向量，矩阵的应用。II单元特征值和特征矢量9小时特征值，特征矢量，Caley-Hamilton定理，矩阵的对角线化，矩阵的二次形式。第三单元差分计算-I 9小时连续的分化，Taylor's＆McLaurin的系列，不确定形式，部分导数，Euler的定理，总导数IV差异单位计算9小时Jacobians＆IT＆Maxima and Maxima and Maxima and Maxima and Mixima of两次多变功能，该功能可实现lagrange的功能。单元V复杂分析9小时的复杂数字，Demovier定理，复杂函数，复杂函数的差异，分析功能，C-R方程，谐波功能教科书：1。B. S. Grewal的高级工程学数学（德里Khanna出版物）。
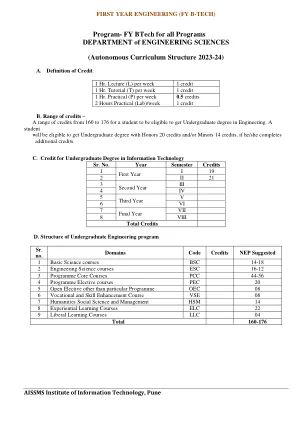
第一年工程（FY B -Tech） - 计划
1。在SEM考试中内部40 2。结束SEM考试外部60总计100先决条件：关于分化，集成和矩阵的合理知识。课程目标：1使用矩阵来发展对线性方程系统的理解。2解释了本征值和本本矢量的概念。3传授函数扩展的知识，平均值定理和不确定形式。4使学生能够理解几个变量功能的衍生物的概念。5介绍雅各布人的合理知识，误差和近似以及两个变量功能的极端值。课程成果：成功完成课程后，学生将能够使用矩阵求解线性方程系统，并将其应用于研究密集术的过程
定向热流体的稳健面向对象公式化...
一种最为突出的应用方法是使用 Modelica 等语言通过微分代数方程系统对流体系统进行面向对象建模。例如，上文应用领域的所有参考文献均指 Modelica 实现，图 1 展示了作为飞机气候系统一部分的空气循环的 Modelica 模型图。Modelica 是一种开放且免费的建模语言 [5]，得到各种商业和免费工具的支持。此外，还有免费的 Modelica 标准库支持不同应用领域的通用物理建模基础：支持各种流体热力学性质模型的媒体库 [6] 和具有通用接口 [8] 的标准流体库 [7]，用于对流经体积元和系统边界之间各种组件的流体流进行建模。
（信息技术）
数学逻辑：命题逻辑；一阶逻辑：概率：条件概率；卑鄙，中位数，模式和标准偏差；随机变量；分布；制服，正常，指数，泊松，二项式。集合理论与代数：集合，关系，功能，群体，部分订单，晶格，布尔代数。组合学：排列，组合，计数，求和，生成功能，复发关系，渐近学。图理论：连通性，跨越树，切割的顶点和边缘，覆盖，匹配，独立集，着色，平面性，同构。线性代数：矩阵的代数，决定因素，线性方程系统，本特征值和本本矢量。数值方法：线性方程系统的LU分解，通过secant，bisection和Newton-Raphson方法的非线性代数方程的数值解；梯形和辛普森规则的数值集成。微积分：极限，连续性和不同性，平均值定理，积分的定理，确定和不当积分的评估，部分衍生物，总导数，Maxima＆Minima。