XiaoMi-AI文件搜索系统
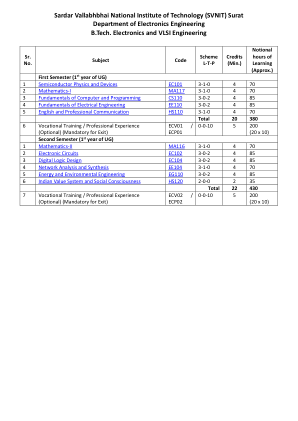
World File Search System电子技术与超大规模集成电路工程学士
3. 教程 1 一阶常微分方程-I 2 一阶常微分方程-II 3 微分方程的应用 4 无限级数-I 5 无限级数-II 6 傅里叶级数-I 7 傅里叶级数-II 8 傅里叶积分与变换-I 9 傅里叶积分与变换-II 10 傅里叶积分与变换-II 11 贝塔函数与伽马函数-I 12 贝塔函数与伽马函数-II 13 线性代数方程组-I 14 线性代数方程组-II 15 线性代数方程组-III
使用深度学习的领域知识来解决应用的反问题
图2:从有或不包含强度定律方程的五个模型的预测孔隙率值的比较:(a)CNN,(b)knn,(c)lstm,(d)RF和(e)xgboost。将强度定律方程组合为输入的图可显着提高预测的准确性,从而与真实的孔隙率值更紧密地对齐。
Hedin方程
hedin的方程式提供了一条优雅的途径,可以通过一组非线性方程式的自洽迭代来计算确切的单体绿色功能(或传播器)。其一阶近似(称为GW)对应于环图的重新介绍,并且在物理和化学方面已显示出非常成功的。通过引入顶点校正,尽管具有挑战性,可以进行系统的改进。 考虑到异常的繁殖器和外部配对电位,我们得出了一组新的自洽的封闭方程组,等于著名的Hedin方程,但作为一阶近似粒子粒子(PP)t -matrix近似值,在其中执行梯子图的重置。 通过考虑低阶PP顶点校正,HedIn方程的PP版本提供了一种系统地超越T -Matrix近似的方法。可以进行系统的改进。考虑到异常的繁殖器和外部配对电位,我们得出了一组新的自洽的封闭方程组,等于著名的Hedin方程,但作为一阶近似粒子粒子(PP)t -matrix近似值,在其中执行梯子图的重置。通过考虑低阶PP顶点校正,HedIn方程的PP版本提供了一种系统地超越T -Matrix近似的方法。
Hedin方程 div>
hedin的方程式提供了一条优雅的途径,可以通过一组非线性方程的自洽迭代来计算确切的一体绿色功能(或传播器)。其一阶近似(称为GW)对应于环图的重新介绍,并且在物理和化学方面已显示出非常成功的。通过引入顶点校正,尽管具有挑战性,可以进行系统的改进。 考虑到异常的传播器和外部配对电位,我们得出了一组与著名的Hedin方程相等的封闭方程组,但作为第一阶近似值,粒子粒子(PP)t -matrix近似值,在此执行梯形图的分解。 通过考虑低阶PP顶点校正,HedIn方程的PP版本提供了一种系统地超越T -Matrix近似的方法。可以进行系统的改进。考虑到异常的传播器和外部配对电位,我们得出了一组与著名的Hedin方程相等的封闭方程组,但作为第一阶近似值,粒子粒子(PP)t -matrix近似值,在此执行梯形图的分解。通过考虑低阶PP顶点校正,HedIn方程的PP版本提供了一种系统地超越T -Matrix近似的方法。
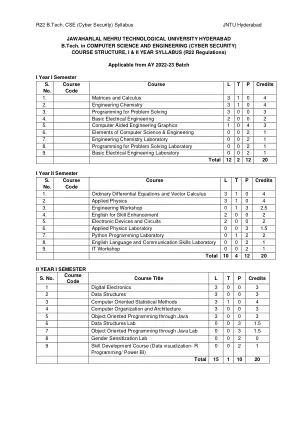
R22 B.Tech. CSE(网络安全)课程大纲
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 评估多重积分并应用概念来寻找面积和体积 UNIT - I:矩阵 10 L 通过梯形和标准形式对矩阵进行秩,通过高斯-乔丹方法对非奇异矩阵进行逆运算,线性方程组:用高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元:特征值和特征向量 10 L 线性变换和正交变换:特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理(无证明)、用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、用正交变换将二次型简化为标准形式。 第三单元:微积分 10 L 均值定理:罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积(仅限于笛卡尔坐标系)、不当积分的定义:Beta 函数和 Gamma 函数及其应用。第四单元:多元微积分(偏微分和应用)10 L 极限和连续性的定义。偏微分:欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用:使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
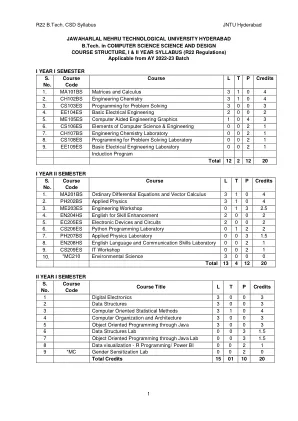
R22 B.Tech. CSE(AI 和 ML)课程大纲 JNTU 海得拉巴
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 评估多重积分并应用概念来寻找面积和体积 UNIT - I:矩阵 10 L 通过梯形和标准形式对矩阵进行秩,通过高斯-乔丹方法对非奇异矩阵进行逆运算,线性方程组:用高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元:特征值和特征向量 10 L 线性变换和正交变换:特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理(无证明)、用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、用正交变换将二次型简化为标准形式。 第三单元:微积分 10 L 均值定理:罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积(仅限于笛卡尔坐标系)、不当积分的定义:Beta 函数和 Gamma 函数及其应用。第四单元:多元微积分(偏微分和应用)10 L 极限和连续性的定义。偏微分:欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用:使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
R22 B.Tech. CSD 教学大纲 JNTU 海得拉巴 1 ...
写出一组线性方程的矩阵表示并分析方程组的解 查找特征值和特征向量 使用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数评估不当积分 找到有/无约束的两个变量函数的极值。 评估多重积分并应用概念来寻找面积和体积 UNIT - I:矩阵 10 L 通过梯形和标准形式对矩阵进行秩,通过高斯-乔丹方法对非奇异矩阵进行逆运算,线性方程组:用高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元:特征值和特征向量 10 L 线性变换和正交变换:特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理(无证明)、用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、用正交变换将二次型简化为标准形式。 第三单元:微积分 10 L 均值定理:罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积(仅限于笛卡尔坐标系)、不当积分的定义:Beta 函数和 Gamma 函数及其应用。第四单元:多元微积分(偏微分和应用)10 L 极限和连续性的定义。偏微分:欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用:使用拉格朗日乘数法求二元和三元函数的最大值和最小值。
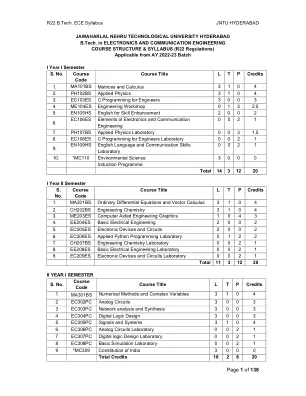
R22 B.Tech. ECE 教学大纲 JNTU 海得拉巴
写出一组线性方程的矩阵表示并分析方程组的解 寻找特征值和特征向量 利用正交变换将二次形式简化为标准形式。 解决均值定理的应用。 使用 Beta 和 Gamma 函数求不当积分 找出有/无约束的两个变量函数的极值。 评估多重积分并应用概念寻找面积、体积 UNIT-I:矩阵 10 L 通过梯形和标准形式对矩阵进行秩计算,通过高斯-乔丹方法对非奇异矩阵进行逆计算,线性方程组:通过高斯消元法、高斯赛德尔迭代法求解齐次和非齐次方程组。第二单元:特征值和特征向量 10 L 线性变换和正交变换:特征值、特征向量及其性质、矩阵对角化、凯莱-汉密尔顿定理(无证明)、利用凯莱-汉密尔顿定理求矩阵的逆和幂、二次型和二次型的性质、利用正交变换将二次型简化为标准形式。 第三单元:微积分 10 L 均值定理:罗尔定理、拉格朗日均值定理及其几何解释和应用、柯西均值定理、泰勒级数。应用定积分求曲线旋转的表面积和体积(仅在笛卡尔坐标系中)、不定积分的定义:Beta 函数和 Gamma 函数及其应用。 UNIT-IV:多元微积分(偏微分和应用)10 L 极限和连续性的定义。偏微分:欧拉定理、全导数、雅可比矩阵、函数依赖性和独立性。应用:使用拉格朗日乘数法求二元和三元函数的最大值和最小值。