XiaoMi-AI文件搜索系统
World File Search System生命周期成本分析
分布式能源系统(DES)作为提高电力和热力生产可持续性能的一种手段,受到越来越多的关注。然而,许多研究表明,分布式能源系统的成本高于传统的集中式能源发电(CCEP)。以往对DES经济分析的研究一般忽略了政策激励、企业折旧和排放税的经济影响。本研究旨在研究在考虑美国政策激励和排放税的影响下,DES的生命周期成本(LCC)的降低情况。我们首先使用参数模型为美国五个气候区下的三种商业建筑类型找到最优的DES解决方案。然后,我们计算了每种情景的LCC,并评估了可行的美国清洁能源政策激励措施的成本节约潜力,包括联邦税收抵免、低息贷款和加速折旧。最后,我们使用空气污染排放实验和政策模型来量化空气污染物排放的社会成本,以制定对DES和CCEP的排放税。结果表明,集中式传统能源生产的社会成本明显高于分布式能源系统。美国一系列可行的清洁能源政策平均可将分布式能源系统的成本降低 67%。假设能源相关排放的社会成本也被考虑在内,并作为能源生产的排放税征收。在这种情况下,与 CCEP 相比,分布式能源系统的 50% 建筑能源供应方案具有成本竞争力。© 2020 Elsevier Ltd. 保留所有权利。
SPP 储能研究
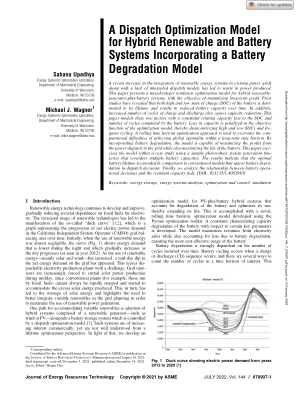
模拟了额外的敏感度,将此设置更改为“经济套利”,以优化经济套利的方式调度电池。SERVM 仍将在高净负荷时段调度电池,但由于该模型无法完美预见发电机性能,因此从可靠性的角度来看,调度可能不是最优的。例如,在高净负荷日,储能资源可能已安排在一天中净负荷最高的时段调度。然后,发电机可能会在高净负荷期结束时随机发生故障,从而产生可靠性事件。由于电池是在高负荷时段调度的,因此它不再可用于防止稳定负荷削减。而“保持可靠性”方法如果不需要防止稳定负荷削减,就不会在高净负荷时段调度。这种比较很重要,因为它说明了在保持可靠性与优化经济性时电池容量信用的权衡。如图 3 所示,经济套利运营策略提供的容量信用低于“保持可靠性”运营策略。在这种情况下,比较仅量化发电机性能的不确定性影响;负荷预测的额外不确定性或可再生能源输出的不确定性将导致经济调度策略和“保持可靠性”策略之间的额外差异。如果发电机性能完全已知,“经济套利”和“保持可靠性”策略将产生相同的结果。
活力
风能 世界领先的风能研究和科学咨询,涵盖陆上和海上风力涡轮机的材料、部件和测试。风能是未来全球能源系统中不可或缺的一部分。 太阳能 在生活实验室(陆地、水中或建筑物内)开发和测试太阳能电池和太阳能电池板,重点是优化系统、功能和性能。 混合动力发电厂 在混合动力发电厂中将风能和太阳能与电池储存和电解相结合。 Power-to-X 世界领先的电解技术和工艺,用于生产氢气、氨、甲醇和航空燃料。 电池 开发电池储存系统和电池新材料,重点是可持续材料和工艺。 热能存储 使用熔盐和石头的高温储热可以确保更可持续的能源,并适应波动的风能和太阳能发电。 新形式的能源 例如,聚变、裂变和地热能的研究、技术开发和实验设施。 综合能源系统 更灵活的能源系统,可以监控和调整能源系统的灵活性。从特定设备到跨国界和跨部门的大型系统,应有尽有。DTU 利用数字化的可能性来研究如何最好地管理生产和消费之间的平衡。弹性能源系统开发解决方案,使能源系统能够抵御极端天气情况、数字和物理威胁。能源市场确保社会经济最优的能源系统,其中技术以公开竞争的方式提供服务。分析有助于我们了解如何在能源市场中最好地实施能源技术。
基于人工智能的功率转换器电路参数设计(AI-D)
摘要 --- 参数设计对于确保功率转换器的整体性能令人满意具有重要意义。通常,功率转换器的电路参数设计包括两个过程:分析和推导过程和优化过程。现有的参数设计方法包括两种类型:传统方法、计算机辅助优化(CAO)方法。在传统方法中,需要严重依赖人。即使新兴的 CAO 方法使优化过程自动化,它们仍然需要手动的分析和推导过程。为了减轻对人的依赖以实现高精度和易于实施,本文提出了一种基于人工智能的设计(AI-D)方法用于功率转换器的参数设计。在提出的 AI-D 方法中,为了实现分析和推导过程的自动化,采用仿真工具和批量归一化神经网络(BN-NN)为优化目标和设计约束构建数据驱动模型。此外,为了实现优化过程的自动化,使用遗传算法来搜索最佳设计结果。所提出的 AI-D 方法在电动汽车 48 V 至 12 V 附件负载电源系统中同步 Buck 转换器的电路参数设计中得到了验证。给出了效率最优的同步 Buck 转换器的设计案例,该转换器在体积、电压纹波和电流纹波方面均有约束。最后,通过硬件实验验证了所提出的 AI-D 方法的可行性和准确性。索引术语 - 功率转换器、参数设计、人工智能、进化算法、神经网络。
基于动态信息分配的联邦过滤器...
多传感器组合导航在水下传感器网络中得到了广泛的应用,它提高了单传感器的跟踪精度,且具有较好的容错能力。多传感器数据融合有两种基本结构:集中式融合和分布式融合。集中式融合将所有数据收集到融合中心进行处理,因此不存在任何数据丢失,集中式融合是最优的,但集中式融合计算和通信负担过重,容错能力差。分布式融合近年来受到越来越多的关注。20世纪90年代,NA Carlson提出了联邦滤波器[1]。联邦滤波器由一个全局滤波器和若干个局部滤波器组成,各局部滤波器彼此独立,采用各自的滤波算法,处理各自的测量信息并生成局部的跟踪路径。全局滤波器只能融合局部滤波器生成的路径[2]。传统的联邦滤波器使用KF作为局部滤波器,这导致传统的联邦滤波器只能跟踪线性运动目标。但测量函数往往是非线性的,KF不能利用非线性信息,因此该算法采用UKF作为局部滤波器。此外,为了识别故障传感器,将动态信息分配设计为子滤波器协方差矩阵的迹与全局协方差矩阵的迹的比值。仿真结果表明,该算法能很好地跟踪非线性系统,且精度优于UKF算法,并且能放大子系统的软故障灵敏度,从而易于识别故障传感器。
结合电池退化模型的混合可再生能源和电池系统调度优化模型
近年来,现有电网中可再生能源系统的整合度不断提高,加上缺乏综合调度模型,导致了电力浪费。本文提出了一种混合可再生发电机加电池系统的混合整数非线性优化模型,目标是最大化长期利润。先前的研究表明,电池的高和低充电状态 (SOC) 都会损害其使用寿命,并会导致电池容量随时间降低。此外,增加充电和放电循环次数也会导致容量降低。本文对这两个因素进行了建模,并将容量损失与 SOC 和电池完成的循环次数联系起来。容量损失在优化模型的目标函数中受到惩罚,从而不鼓励高和低 SOC 以及频繁循环。滚动时间范围优化方法用于克服在长期时间范围内实现全局最优的计算困难。通过考虑电池退化,该模型能够最大限度地提高电力调度到电网的利润,同时最大限度地延长电池的使用寿命。本文使用考虑多种电池容量的光伏系统发电时间序列样本,在案例研究中运用了该模型。结果表明,与在调度决策中忽略电池退化的传统模型相比,最佳电池寿命有所延长。最后,我们分析了电池操作决策与由此产生的容量衰减之间的关系。[DOI:10.1115/1.4052983]
超越偶极子近似的量子控制领域:可控性、奇异控制和资源
我们通过在哈密顿量中加入极化项来研究超出偶极近似的封闭 n 级量子系统的控制景观。后者在控制场中是二次的。对奇异控制进行了理论分析,奇异控制是产生景观陷阱的候选对象。将考虑奇异控制存在的结果与偶极近似(即没有极化)中的结果进行了比较。在加入极化项后,对控制景观中陷阱的存在进行了数值分析,以产生超出偶极近似的幺正变换。通过创建许多随机哈密顿量(在单个控制场中包含线性和二次项),对这些控制景观进行了广泛的探索。发现的奇异控制都不是局部最优的。这一结果扩展了最近关于进行偶极近似的量子系统典型景观的大量研究。我们进一步研究了极化率的大小与优化产生的控制通量之间的关系。结果还表明,在原本不可控的偶极耦合系统中加入极化率项可以通过恢复可控性从相应的控制景观中移除陷阱。我们用数字方式评估了极化率项对特定三级 3 系统已知示例的影响,该系统的控制景观中有一个二阶陷阱。结果发现,极化率的增加会从景观中移除陷阱。讨论了这些模拟的一般实际控制含义。
最优自给自足区技术经济分析
许多城市和地区都宣布,他们的最终目标是实现能源自给自足,但还有许多技术和经济挑战需要研究。本研究的目的是为能源自给自足率高的地区找到成本最优的技术解决方案,以满足其电力需求。采用两种方法,一种是基于规则的方法,一种是优化方法,以找到一个地区中具有最低生命周期成本的本地集中风电、太阳能光伏、电池、热存储和热泵的可再生能源系统容量。以芬兰赫尔辛基的卡拉萨塔玛区为例。结果表明,完全能源自给自足的目标需要在可再生能源系统上进行非常高的投资。对于所研究的案例,将自给自足率降低到 76% 可以将生命周期成本降低 66%,并实现净零年度能源平衡。从经济和技术上讲,实现正能源区或净零能源区比实现完全能源自给自足更为可行。根据所得结果,主要投资应放在风电上,因为与太阳能光伏相比,风电全年利用率更高。当自给率从 100% 降低时,对昂贵的集中式电池存储的投资将急剧下降。结果表明,由于人口密度高和可再生能源供应有限,如果以高自给率为目标,一个地区的物理边界可能不适合所需的可再生能源设施。这通常会导致将地区边界扩大到虚拟平衡边界。
直流 OPF 中具有互补约束的并网储能系统模型的凸松弛
可再生能源的间歇性是将可再生能源发电整合到电网的主要挑战之一。可再生能源的变化或可用的可再生能源预测误差可以通过在电网中纳入分布式能源存储系统 (ESS) 来解决 [1]–[4]。与电网连接的 ESS 的优势包括削减峰值负荷和降低发电机爬升率。然而,在将 ESS 模型纳入优化问题时,特别是凸最优潮流 (DC OPF) 问题,由于使用无损 ESS 模型 [5] 或非凸 ESS 操作模型,需要使用计算限制方法 [3],[6],因此确保适当的 ESS 动态可能会受到很大限制。在本文中,我们对与电网连接的 ESS 模型的凸松弛进行了分析,该模型在 DC OPF 问题中有单独的充电和放电项。我们考虑一个一般的直流 OPF 问题,它协调传统发电机、分布式可再生能源和受网络功率流约束的 ESS,以满足网络负载,同时最小化发电成本并考虑发电容量约束。在这项工作中,我们使用 Karush Kuhn-Tucker (KKT) 条件来展示何时解决科学问题,科罗拉多大学博尔德分校,科罗拉多州博尔德,80309 美国(电子邮件:{kaitlyn.garifi; kyri.baker}@colorado.edu)。当使用建议的放松 D. Christensen 时,ESS 同时充电和放电的直流 OPF 问题不是最优的,他是国家可再生能源实验室的成员,科罗拉多州戈尔登,80401 美国(电子邮件:dane.christensen@nrel.gov)
北京大学量子材料科学中心 - International Center for Quantum ...
在非相对论量子系统中,利布-罗宾逊定理 [1-2] 规定了一个新出现的速度限制 v,在幺正演化下建立了局部性,并限制了执行有用量子任务所需的时间。在本次演讲中,我将介绍我们的工作 [3],即将利布-罗宾逊定理扩展到具有测量和自适应反馈的量子动力学。与测量可以任意违反空间局部性的预期相反,我们发现量子信息的速度最多可以提高 (M+1) 倍,前提是已知 M 个局部测量的结果;即使经典通信是即时的,这也是如此。我们的界限是渐近最优的,并且被现有的基于测量的协议所饱和 [4]。我们严格限制了量子计算、纠错、隐形传态以及从短程纠缠初始状态生成纠缠资源状态(Bell、GHZ、Dicke、W 和自旋压缩状态)的资源要求。我们的研究结果限制了使用测量和主动反馈来加速量子信息处理,并限制了大量已提出的量子技术的可扩展性。参考文献:[1] Lieb 和 Robinson,“量子自旋系统的有限群速度”,Comm. Math. Phys. 28, 251 (1972)。[2] Chen, Lucas 和 Yin,“多体量子动力学中的速度限制和局部性”,arXiv:2303.07386。[3] Friedman, Yin, Hong 和 Lucas,“带测量的量子动力学中的局部性和误差校正”,arXiv:2206.09929。[4] Briegel, Dur, Cirac 和 Zoller,“量子中继器:不完美局部操作在量子通信中的作用”,Phys. Rev. Lett. 81, 5932 (1998)。