XiaoMi-AI文件搜索系统
World File Search System期望值
工程师量子科学入门
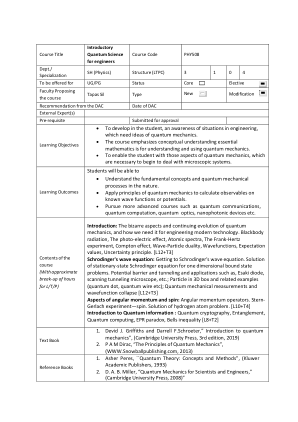
简介：量子力学的奇异方面和持续发展，以及我们如何需要它来设计现代技术。黑体辐射、光电效应、原子光谱、弗兰克-赫兹实验、康普顿效应、波粒二象性、波函数、期望值、不确定性原理。[L12+T3] 薛定谔波动方程：了解薛定谔波动方程。一维束缚态问题的稳态薛定谔方程解。势垒和隧穿以及诸如 Esaki 二极管、扫描隧道显微镜等应用；3D 盒子中的粒子和相关示例（量子点、量子线等）；量子力学测量和波函数坍缩 [L12+T3] 角动量和自旋方面：角动量算子。斯特恩-格拉赫实验 - 自旋。氢原子问题的解。 [L10+T4] 量子信息简介：量子密码学、纠缠、量子计算、EPR悖论、贝尔不等式 [L8+T2]
量子状态的经典和混合阴影
经典阴影是一种在经典计算机上存储量子状态的计算有效方法，目的是估算通过执行重复的随机测量获得的局部观测值的期望值。在本说明中，我们就此方法提供了一些评论。我们注意到，与有限的相对误差形成分类阴影所需的资源在很大程度上取决于目标状态。然后，我们对使用经典阴影模拟多个身体动态的优点和局限性发表评论。此外，我们介绍了由系统的一部分上的测量而不是整体构建的混合阴影的概念，该框架提供了一个框架，以更深入地了解阴影状态的性质，因为一个人降低了测量的子系统的大小，并且可以替代了压缩量子状态的潜在替代方案。
对量子近似优化算法进行基准测试
摘要 使用三个不同的指标来评估量子近似优化算法的性能：找到基态的概率、能量期望值和与近似比密切相关的比率。所研究的问题实例集包括加权 MaxCut 问题和 2 可满足性问题。后者的 Ising 模型表示具有独特的基态和高度简并的第一激发态。量子近似优化算法在量子计算机模拟器和 IBM Q Experience 上执行。此外，使用从 D-Wave 2000Q 量子退火器获得的数据进行比较，发现 D-Wave 机器的性能优于在模拟器上执行的量子近似优化算法。发现量子近似优化算法的整体性能在很大程度上取决于问题实例。
ph1107.pdf
基础量子力学（BQM）：11. 在量子力学的背景下解释算子、状态、特征值和特征函数这些术语（首先针对双态系统，然后扩展到具有连续特征值的系统），并确定物理量的期望值和不确定性。12. 确定给定势阱（例如无限势阱和屏障）中粒子的波函数，并列举其在技术中的应用示例（例如量子点显示器、存储设备）。13. 使用特征函数的正交性并对叠加中的量子系统进行基本分析。14. 讨论量子现象（例如量子叠加、波函数坍缩、量子隧穿和海森堡不确定性原理），并解释它们与我们对现实的感知的冲突。15. 使用氢原子的量子数：n、l、m 确定相应的特征函数（来自给定的表格）并解决相关的简单问题。课程内容 基础（FND） 波的性质 光速 叠加、衍射和干涉 原子和亚原子粒子 狭义相对论（SR） 参考系和伽利略变换 狭义相对论和洛伦兹变换的假设 长度收缩和时间膨胀 闵可夫斯基时空图 解决悖论 相对论动量、动能和能量 基础核物理（BNP） 放射性粒子（𝛼，𝛽 𝑝𝑎𝑟𝑡𝑖𝑐𝑙𝑒𝑠 𝑎𝑛𝑑 𝛾−𝑟𝑎𝑑𝑖𝑎𝑡𝑖𝑜𝑛） 核裂变和聚变 放射性 质能当量 医学应用和剂量 量子物理（QP） 黑体辐射物理量的量化光电效应康普顿散射和波长对的产生/湮没双缝实验戴维森-杰默实验波粒二象性氢原子（玻尔模型和原子光谱）基础量子力学（BQM）特征值、特征函数和算子两能级系统薛定谔方程和波函数概率（密度）无限和有限势阱（盒子中的粒子）量子谐振子势垒/台阶期望值和不确定性
![arXiv:2407.17405v3 [quant-ph] 2024 年 10 月 8 日](/simg/4\48778b8f99287d8b2fcda042a71bd4cabf82e375.webp)
arXiv:2407.17405v3 [quant-ph] 2024 年 10 月 8 日
张量网络和量子计算是模拟量子多体系统最强大的两种工具。我们并不将它们视为相互竞争的方法，而是在此考虑如何协同工作这两种方法。我们引入了一种新算法，该算法结合了张量网络和量子计算，产生的结果比单独使用其中任何一种方法所能获得的结果更准确。我们的算法基于多积公式 (MPF) - 一种线性组合 Trotter 积公式以减少算法误差的技术。我们的算法使用量子计算机计算期望值，使用张量网络计算线性组合中使用的系数。我们对该算法进行了详细的错误分析，并使用两台 IBM 量子计算机：ibm_torino 和 ibm_kyiv 演示了 50 量子比特的一维量子模拟问题的完整工作流程。
使用差异形式的量子机械预期值推导
摘要通常是各种物理量的预期值，例如占据某些状态的电子数量或不同电子状态之间的库仑相互作用，可以用积分来表示。相比之下，我们的方法基于差异形式，表明可以通过平均时间来获得期望值。确认我们方法的有效性，我们准备了两种情况：一个是一个非常简单的情况，没有多体相互作用，另一种是包含多体项的情况（最简单的安德森·哈密顿式）。关于简单的情况而没有包含多体项，我们可以分析地证明，占据从我们方法得出的任何状态的电子数量等同于从绿色功能方法中评估的分析。包括多体项时，我们的结果显示了与绿色功能方法得出的分析方法的良好数值一致。通过两种情况，基于我们方法的预期值计算被认为是有效的。
近期量子计算机的读数重新平衡
读数错误是近期中级量子计算机的噪声源。误以为| 1⟩当应该是| 0⟩的发生频率要少得多，而不是量子不当| 0⟩当它应该是| 1⟩。我们简单地观察到，可以通过在进行测量之前应用目标X大门来改善量子计算机的读数。放置了这些X门，以便| 1⟩状态最小化。经典的后处理可以消除X门的效果，以使任何可观察到的可观察到的期望值保持不变。该协议的设计是在读数错误对称时没有效果。我们表明，使用读数重新平衡时，读数错误校正后的统计不确定性较小。统计优势是电路和计算机依赖性的，并且用于W状态，Grover搜索以及高斯状态。当统计精度中的好处最为明显（在某些情况下几乎是2倍），而在激发状态中有许多Qubit的状态具有很高的概率。
蒙特卡洛树搜索的量子加速
Monte Carlo Tree Search（MCTS）是一种随机计划算法，可以为两人游戏中的动作提供建议，而无需启发式启发式。在这项工作中，我们描述了一种量子算法，以加快在执行多个此类推出的MCT变体中执行的随机“随机推出”步骤。引入了另一种量子算法，该算法加快了MCTS实例集合的计算。作为开发的技术的推论，提出了一种量子算法，用于估算任意（随机）长度的保单引导在任意（随机）环境中的期望值或最大化的第一步。此步行是由初始状态，策略函数和过渡功能定义的，其值通过在所采用的完整路径上定义的任意评估功能分配给了这样的walk。相对于最著名的经典算法，发现的所有加速度都是二次的。
PT 对称、非厄米量子多体物理学...
我们回顾了从理论上处理宇称时间 (PT) 对称非厄米量子多体系统的方法。它们被实现为具有 PT 对称性并与环境相容的耦合的开放量子系统。PT 对称非厄米量子系统表现出各种迷人的特性，使它们在一般的开放系统中脱颖而出。后者的研究在量子理论中有着悠久的历史。这些研究基于组合系统-储层装置的厄米性，由原子、分子和光学物理学以及凝聚态物理学界开发。数学物理学界对 PT 对称非厄米系统的兴趣导致了新的视角和 PT 对称和双正交量子力学优雅数学形式主义的发展，这些形式主义不涉及环境。在数学物理研究中，重点主要放在哈密顿量的显着光谱特性和相应单粒子本征态的特征上。尽管哈密顿量不是厄米量的，但它们可以显示所有特征值都是实数的参数区域。然而，为了研究凝聚态物理中出现的量子多体现象并与实验取得联系，人们需要研究可观测量和关联函数的期望值。此外，人们必须研究统计集合而不仅仅是特征态。凝聚态界部分人士采用 PT 对称和双正交量子力学的概念，导致该方法论处于争议之中。对于一些基本问题，例如，什么是适当的可观测量，如何计算期望值，什么是充分的平衡统计集合及其相应的密度矩阵，人们并没有达成共识。随着工程和控制开放量子多体系统的技术进步，现在是时候将厄米量与 PT 对称和双正交观点相协调了。我们全面回顾了不同的方法，包括伪厄米性的过度思想。为了激发我们在这里宣传的厄米观点，我们主要关注辅助方法。它允许将非厄米系统嵌入到更大的厄米系统中。与其他技术（例如主方程）相比，它不依赖于任何近似值。我们讨论了 PT 对称和双正交量子力学的特性。在这些中，被认为是可观测量的东西取决于哈密顿量或选定的（双正交）基。此外，至关重要的是，被称为“期望值”的东西缺乏直接的概率解释，而被视为正则密度矩阵的东西是非平稳和非厄米的。此外，时间演化的非幺正性隐藏在形式主义中。我们选取了几个模型哈密顿量，到目前为止，这些模型要么是从厄米角度研究的，要么是从 PT 对称和双正交角度研究的，并在各自的替代框架内研究它们。这包括一个简单的两级单粒子问题，但也包括显示量子临界行为的多体晶格模型。比较这两种计算的结果，可以发现厄米方法虽然在某些方面很笨拙，但总能得出物理上合理的结果。在极少数情况下，如果可以与实验数据进行比较，它们还会一致。相比之下，数学上优雅的 PT 对称和双正交方法得出的结果在一定程度上难以物理解释。因此，我们得出结论，厄米方法应该是
基于直流微电网的混合储能系统能量管理与控制策略
本文介绍了一种独立直流微电网中与存储设备共享的能源管理方法。管理的目的是满足能源需求，同时保证生产/消耗平衡，并具有良好的直流母线电压调节和稳定性。该能源管理方法的另一个优点在于通过计算公共直流母线上的有效功率来考虑静态转换器中的损耗。所提出的控制策略利用非线性控制，结合模糊逻辑控制来从光伏和风能源中提取最大功率，同时使用滑模控制来控制存储功率转换器。公共直流母线功率流的控制使母线电压具有良好的稳定性，在期望值附近的偏差很小，从而限制了电池应力，因为低频电流分量被发送到电池，而高频功率分量被导向超级电容器。仿真结果证明了所提出的能源管理和控制策略的有效性。