XiaoMi-AI文件搜索系统
World File Search System椭圆
椭圆曲线（用于加密术）
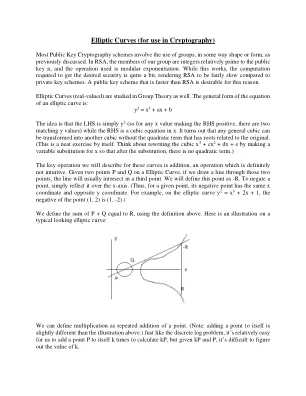
的想法是LHS仅是y 2（因此，对于使RHS呈阳性的任何X值，有两个匹配的Y值），而RHS是x中的立方方程。事实证明，任何一般立方都可以转变为另一立方体，而没有与原始词根相关的二次术语。（这本身就是一个整洁的练习。考虑通过对X进行可变替换来重写Cutic X 3 + CX 2 + DX + E我们将为这些曲线描述的关键操作是添加的，这绝对不是直观的。在椭圆曲线上给定两个点P和Q，如果我们通过这两个点绘制一条线，则该线通常将在第三点相交。我们将这一点定义为-r。要否定点，只需将其反映在X轴上即可。（因此，对于给定点，其负点具有相同的x坐标和相对的Y坐标。例如，在椭圆曲线y 2 = x 3 + 2x + 1上，点（1，2）的负为（1，-2）。）我们使用上面的定义定义了P + Q等于R的总和。这是典型外观椭圆曲线的插图：
椭圆法和极化法
椭圆法是一种成熟的实验方法，其根部回到了现代光学元件本身的早期阶段。它通常是由保罗·德鲁德（Paul Drude）在19世纪的最后十年中发明的，但是在Drude开始工作之前已经采用了类似的技术。自1940年代以来使用的实际术语“椭圆法”正在使用。有趣的是，它始于描述生物应用的工作。值得注意的是，这是在一个现代实心相，尤其是半导体材料的现代物理学正在迅速扩展。椭圆形即将受到固态和表面研究界的欢迎，因为研究表面，界面和薄层的能力是必不可少的。椭圆法是一种从数值计算和建模概念中受益匪浅的方法。固态物理和椭圆法之间的连接是科学和技术中自我强化创新周期的一个例子。尤其是在计算能力wasaccompaniedwithanincreasefellipsometryresearch和社区的迅速扩展的情况下，大大增加了。椭圆法 - 微电子和数字技术。反之亦然，它可以开发更好的电子设备。如果没有椭圆计的开发及其数十年前的许多折叠应用，那是数字时代的基础将不存在的硬件。椭圆法是对反射实验的偏振法实现。所有偏振技术都取决于
基于深度学习的二维椭圆框区域脑肿瘤分割可行性研究
摘要：在大多数基于深度学习的脑肿瘤分割方法中，训练深度网络需要带注释的肿瘤区域。然而，准确的肿瘤注释对医务人员提出了很高的要求。本研究的目的是利用肿瘤周围的椭圆框区域训练深度分割网络。在所提出的方法中，深度网络通过使用大量未注释的肿瘤图像（其中肿瘤和背景周围有前景（FG）和背景（BG）椭圆框区域）以及少量带有注释肿瘤的患者（<20）来训练。训练首先在未注释的 MRI 上的两个椭圆框上进行初始训练，然后在少量带注释的 MRI 上进行细化训练。我们使用多流 U-Net 进行实验，它是传统 U-Net 的扩展。这使得能够使用来自多模态（例如 T1、T1ce、T2 和 FLAIR）MRI 的互补信息。为了验证所提方法的可行性，在两个胶质瘤数据集上进行了分割实验与评估，并将在测试集上的分割性能与在相同网络但完全由带注释的MRI图像训练的分割性能进行比较。实验表明，所提方法在测试集上获得了良好的肿瘤分割结果，其中在MICCAI BraTS'17和US数据集上肿瘤区域的dice得分为（0.8407，0.9104），肿瘤区域的分割准确率分别为（83.88%，88.47%）。与使用所有带注释的肿瘤训练的网络的分割结果相比，所提方法在MICCAI和US测试集上的分割性能下降分别为（0.0594，0.0159）和（8.78%，2.61%），但下降幅度相对较小。我们的案例研究表明，使用椭圆框区域代替所有注释的肿瘤来训练网络进行分割是可行的，并且可以被视为一种替代方案，这是在节省医学专家注释肿瘤的时间和分割性能的轻微下降之间的权衡。
二进制椭圆曲线的另一个具体量子隐式分析
摘要。本文为二进制椭圆曲线提供了具体的量子密码分析，以实现时间效率的实现透视（即减少电路深度），并补充Banegas等人的先前研究，该研究的重点是空间效率的效率（即电路宽度）。为了实现深度优化，我们提出了改进Karatsuba乘数和基于FLT的反转的现有电路实现，然后在Qiskit Quantum Computer Simulator中构建和分析资源。提出的乘数架构，改善了Van Hoof等人的量子Karatsuba乘数，减少了与O（n log 2（3））界限的深度和较低的CNOT门，同时保持了相似数量的to效应和鸡蛋。此外，我们所证明的基于FLT的反演会减少CNOT数量和整体深度，并具有较高的量子量。最后，我们采用了拟议的乘数和基于FLT的IN-版本来执行二进制点添加的量子隐性分析以及用于椭圆曲线离散对数问题（ECDLP）的完整shor的算法。结果，除了减小深度外，与先前的工作相比，我们还能够降低多达90％的to oli门，从而显着改善，并提供对量子密码分析的新见解，以实现高度优化的实施。
![OPF使用改进的CHG优化算法
i遗传证据强烈支持管理体重和...
确实“外部集中”视觉生物反馈促进...
革命性的早期疾病检测：阿曼2型糖尿病筛查的高临界性4D CNN模型
机器学习驱动的Web-POST屈曲阻力预测高强度钢梁具有基于椭圆形的Web开口
建筑物的体现碳排放
评估健康和神经退行性衰老中的执行功能能力 - 选择性文献评论
混合储能系统的进步
arxiv：2404.09011v1 [cs.cv] 2024年4月13日
环境管理杂志
多类分类的机器学习软件工具
在covid-... 的年轻人中自我报告的担忧](/simg/3/3719b785dd1ea833df62e0c23311a7f2f0c379fa.webp)
OPF使用改进的CHG优化算法 i遗传证据强烈支持管理体重和... 确实“外部集中”视觉生物反馈促进... 革命性的早期疾病检测：阿曼2型糖尿病筛查的高临界性4D CNN模型 机器学习驱动的Web-POST屈曲阻力预测高强度钢梁具有基于椭圆形的Web开口 建筑物的体现碳排放 评估健康和神经退行性衰老中的执行功能能力 - 选择性文献评论 混合储能系统的进步 arxiv：2404.09011v1 [cs.cv] 2024年4月13日 环境管理杂志 多类分类的机器学习软件工具 在covid-... 的年轻人中自我报告的担忧
摘要：本文介绍了最近开发的饥饿游戏搜索（HGS）优化算法的应用。HGS与混乱的地图相结合，提出了新的混乱饥饿游戏搜索（CHGS）。它用于解决最佳功率流（OPF）问题。OPF的解决方案是为了最大程度地减少发电成本，同时满足了系统的约束。此外，本文为混合可再生能源，光伏和风电场提供了最佳选址。此外，还研究了添加可再生能源对整体发电成本价值的影响。优化问题的探索场是每个研究系统中每个发电机的主动输出功率。CHG还获得了最佳的候选设计变量，该变量对应于最低可能的成本函数值。通过对两个标准IEEE系统进行模拟的20个独立时间-IEEE 57-BUS和118-BUS系统，可以验证引入的CHGS算法的鲁棒性。获得并分析了所获得的结果。基于CHG的OPF被发现具有竞争力，并且优于用于解决文献中相同优化问题的其他优化算法。本文的贡献是在应用于OPF问题时测试对所提出的方法的改进，以及在引入的目标函数上添加可再生能源的研究。
使用椭圆机开发亚极量测试以预测 VO2MAX
这篇硕士论文-开放获取由西密歇根大学 ScholarWorks 研究生院免费提供给您，供您开放获取。它已被西密歇根大学 ScholarWorks 的授权管理员接受，并被纳入硕士论文。有关更多信息，请联系 wmu-scholarworks@wmich.edu 。
Leicns-PK3.0模拟的见解 农业中CRISPR-CAS系统的鸟类视图 将Tikhonov正则化方法应用于低k介电椭圆形孔隙法的问题 泌尿生殖器癌的自适应免疫 通过使用多边形扫描仪在太阳能电池制造中的激光系统的吞吐量限制 DNA聚合酶和生物技术应用 使用结构MRI区分常见的PSP表型：一项机器学习研究 X射线图像的视觉XAI方法可靠性的研究 kurze geschichte der molekularbiologie 胰腺癌的临床免疫疗法
摘要预测脑药代动力学对于中枢神经系统（CNS）药物发展至关重要，但由于人脑抽样的伦理限制，很难。CNS药代动力学（PK）培养物经常因疾病特异性病理生理学而改变中枢神经系统疾病。我们先前发表了一个综合的基于生理的PK（PBPK）模型，该模型预测了大脑和脑脊液室室的小药物的PK pro纤维。在这里，我们改善了这种模型，其大脑非特异性结合和pH对药物电离和被动转运的影响。我们将此改进的模型称为Leiden CNS PBPK预测指标v3.0（leicns-pk3.0）。leicns-pk3.0预测了大鼠和人类中脑ECF和CSF室的未结合浓度，误差少于两倍。然后，我们应用Leicns-PK3.0来研究改变脑脊髓液（CSF）动力学，CSF体积和流动的影响，对脑外细胞外溶液（ECF）药物的影响。使用LEICNS-PK3.0模拟了CSF动力学改变的六种药物的影响，并比较了脑ECF和Lumbar CSF的导致药物暴露。模拟结果表明，改变的CSF动力学改变了CSF PK PROFERES，但并没有改变脑ECF Pro File，而不论该药物的物理化学特性如何。我们的分析支持腰CSF药物浓度不是脑ECF的准确替代的观念，尤其是在中枢神经系统疾病中。系统方法可以说明CNS复杂性的多个级别，并且更适合预测脑PK。
光活性对组成波板的Mueller矩阵椭圆法的影响
摘要：Mueller矩阵椭圆测量法已用于精确表征石英波板，用于在半导体行业苛刻的应用和高精度偏光仪。我们发现这种实验技术对使用是有益的，因为它使我们能够在宽光谱范围内获得绝对和精确的延迟测量，波浪板方向以及复合波板调节。在本文中，证明了在Mueller矩阵模型和数据处理中包括光活性的必要性。尤其是，石英的光活性会影响化合物双重垂直方向波动板之间的未对准的调整。我们证明，从模型中省略光学活性会导致未对准的值不准确。此外，模型中包括有限单色带宽引起的去极化效应。将光活性纳入Mueller矩阵模型已需要基于适当的本构方程的严格理论发展。已将广义的YEH的基质代数与双异型培养基用于计算具有减少对称性的手性材料中的本本征传繁殖。基于应用方法，作者提出了代表光学波动板和双座的Mueller矩阵的近似分析形式，并提供了有关该方法的分析和数值限制的讨论。