机构名称:
¥ 1.0
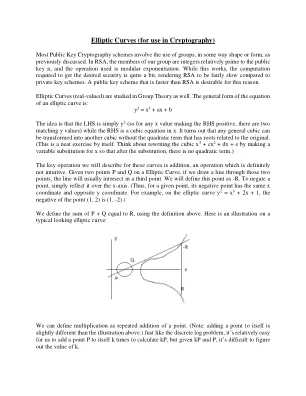
的想法是LHS仅是y 2(因此,对于使RHS呈阳性的任何X值,有两个匹配的Y值),而RHS是x中的立方方程。事实证明,任何一般立方都可以转变为另一立方体,而没有与原始词根相关的二次术语。(这本身就是一个整洁的练习。考虑通过对X进行可变替换来重写Cutic X 3 + CX 2 + DX + E我们将为这些曲线描述的关键操作是添加的,这绝对不是直观的。在椭圆曲线上给定两个点P和Q,如果我们通过这两个点绘制一条线,则该线通常将在第三点相交。我们将这一点定义为-r。要否定点,只需将其反映在X轴上即可。(因此,对于给定点,其负点具有相同的x坐标和相对的Y坐标。例如,在椭圆曲线y 2 = x 3 + 2x + 1上,点(1,2)的负为(1,-2)。)我们使用上面的定义定义了P + Q等于R的总和。这是典型外观椭圆曲线的插图:
椭圆曲线(用于加密术)
主要关键词