XiaoMi-AI文件搜索系统
World File Search System使用结构化波包控制到达时间
研究了具有相同动量密度的高斯和非高斯波包的散射动力学。计算了从方形屏障散射的波包的平均到达时间延迟、停留时间和相位时间延迟,结果表明非高斯波包的平均到达时间延迟与高斯波包不同。这些差异是由非高斯波包的动量波函数相位中的非线性项引起的,这改变了波包的自相互作用时间。可以通过调整动量波函数相位来控制平均到达时间延迟,与波包能量和动量密度无关。
量子力学 – I
然而,此时出现了一个新问题,因为我们不知道任何量子力学状态的精确数学描述,即波函数;而算符需要量子力学状态的绝对数学描述才能产生任何实际结果。现在,虽然我们知道第二条公设提出的不同算符的表达式,但第一条公设只提到存在一个单值、连续和有限的数学函数,但并没有给出实际函数本身;如果没有实际“波函数”的知识,算符几乎毫无用处。因此,人们会认为必须有某种途径可以先获得波函数,然后再将其用作操作数。然而,找到各种量子力学状态的精确数学描述的过程在某种程度上更具协同性。“神奇的奥秘”是,除了最著名的“哈密尔顿算符”之外,所有算符都需要定义量子力学状态的波函数的绝对表达。哈密尔顿算符的特殊之处在于,它不一定需要绝对形式,而只需要符号形式即可产生其物理属性(即能量)的值。然而,在将哈密顿算子应用到波函数的符号形式上时,也得到了绝对表达式。从数学上讲,
量子现实:量子力学测量问题解释的比较分析
摘要 摘要 本文探讨了量子力学中的测量问题,并评估了三种主要解释:哥本哈根解释、多世界解释 (MWI) 和导航波理论。哥本哈根解释认为,粒子在被测量之前处于叠加状态,此时它们的波函数会崩溃。MWI 认为,所有可能的结果都发生在宇宙中独立、不相互作用的分支中,从而消除了波函数崩溃,但引入了无数个不可观测的宇宙。导航波理论通过隐藏变量重新引入了决定论,引导粒子沿着确定的路径行进。本文的结论是,哥本哈根解释是最合理的,它平衡了经验充分性、本体论清晰度和简单性。
量子认知是否意味着量子思维?
量子认知是基于量子理论的数学原理构建认知模型的理论框架。由于量子认知在解释认知科学中自相矛盾的经验发现方面取得了成功,近年来它受到了广泛关注(参见 Wang 等人,2013 年;Busemeyer 和 Bruza,2014 年;Yearsley 和 Busemeyer,2016 年的有益评论)。然而,量子认知模型能告诉我们认知的根本过程仍不得而知。人们普遍认为量子认知只是一种有效的认知理论,其中实际的大脑处理可能以本质上经典的方式进行。在本文中,我们将解决这个问题。基于量子基础研究的最新进展,特别是关于波函数真实性的 PBR 定理,我们将表明分配给认知系统(例如我们的大脑)的波函数,它用于
femtosecond- ...
读取单光子的量子信息通常是通过量子断层扫描或直接(弱)测量方法来实现的。然而,由于严格的时间模式匹配要求,这些方法在表征超快光源的单个光子方面表征单个光子时面临巨大的挑战。在这里,我们使用自我引用干涉仪从连续波源和飞秒光源中从连续波源和飞秒光源中检索了无法区分的单个光子的空间波函数。我们的方法仅需要九个合奏平均测量。该技术简化了单光子波函数的测量过程,并自动模式与每个自身纠正单个光子匹配,从而可以从超快光源中测量单个光子的空间波函数。
通过波导连接的两个开放量子比特腔系统中的几何相位控制
开放量子系统、量子比特-场相互作用的数学操控取决于对主阻尼 [1] 和内在退相干 [2] 方程的分析/数值求解能力。为了解决这些操控问题,在有限的物理环境下研究了开放系统的量子现象 [3-7]。量子几何相是量子力学中的一个基本内在特征,是量子计算的基础 [8]。如果最终的时间相关波函数回到其初始波函数,则量子系统的演化(从初始波函数到最终的时间相关波函数)是周期性的。当这些量子系统的演化不是周期性的时,几何相不再表现出稳健性,所关注的相关量是总相位,称为 Pancharatnam 几何相 (PGP) [9]。PGP 的物理含义是初始状态和最终状态发生干涉,内积的振幅反映了状态之间的相位差。 PGP 在中子干涉仪中实验性地进行了 [10,11]。此后,Berry [12] 在绝热系统中明确定义了几何相,并将其扩展到非绝热循环 [13] 和非循环 [14,15] 演化的量子态。几何相被提出用来实现不同量子模型的几何量子计算,例如:离子阱 [16]、腔场中的原子 [17] 和超导电路 [18]。时间相关的几何相在更多的物理模型中得到了研究,例如:腔 QED 模型充满了非线性介质并包含量子阱 [19],相位量子比特色散耦合到有损 LC 电路的模型 [20] 和具有斯塔克位移的囚禁离子模型 [21]。描述位于孤立腔体中的量子比特之间传输量子态的物理模型,这些量子比特通过光纤模式连接,是构建量子网络的有效系统。在单光子级量子通信中,光纤的使用取得了重大进展 [ 22 ]。这些模型对于设计
使用收缩量子特征求解器对玻色子进行量子模拟
摘要 量子计算机是模拟多体量子系统的有前途的工具,因为它们比传统计算机具有潜在的扩展优势。虽然人们在多费米子系统上投入了大量精力,但在这里我们用收缩量子特征求解器 (CQE) 模拟了一个模型纠缠的多玻色子系统。我们通过在量子比特上编码玻色子波函数将 CQE 推广到多玻色子系统。CQE 为玻色子波函数提供了一个紧凑的假设,其梯度与收缩薛定谔方程的残差成正比。我们将 CQE 应用于玻色子系统,其中 N 个量子谐振子通过成对二次排斥耦合。该模型与量子设备上分子系统中耦合振动的研究有关。结果表明,即使在存在噪声的情况下,CQE 也能以良好的精度和收敛性模拟玻色子过程(例如分子振动)。
使用生成机器学习求解配置空间中的薛定谔方程
图 1:(a) 受限玻尔兹曼机 (RBM) 架构由一个可见输入层和一个二进制值隐藏层组成;对于给定的配置 (v, h),参数 (a, b, W) 用于定义能量函数 E 和相关的类玻尔兹曼概率密度 P。(b) 例如,RBM 可以在一组手写数字上进行训练,然后用于生成新的真实数字;为此,数字图像被展平为一维二进制向量 v(k),其中 1 和 0 分别对应数字和背景像素。(c) 配置相互作用 (CI) 方法将分子的波函数展开为激发斯莱特行列式的线性组合,可以表示为一种一维二进制图像。 (d) 本研究中提出的 CIgen 算法以迭代方式训练 RBM 在波函数当前近似中的行列式分布上,然后通过生成新的贡献来扩展它。
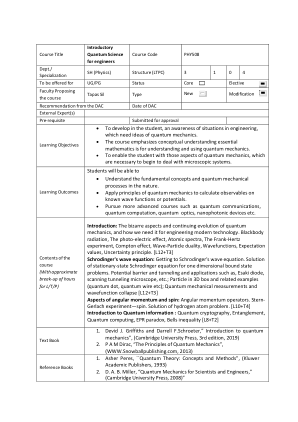
工程师量子科学入门
简介:量子力学的奇异方面和持续发展,以及我们如何需要它来设计现代技术。黑体辐射、光电效应、原子光谱、弗兰克-赫兹实验、康普顿效应、波粒二象性、波函数、期望值、不确定性原理。[L12+T3] 薛定谔波动方程:了解薛定谔波动方程。一维束缚态问题的稳态薛定谔方程解。势垒和隧穿以及诸如 Esaki 二极管、扫描隧道显微镜等应用;3D 盒子中的粒子和相关示例(量子点、量子线等);量子力学测量和波函数坍缩 [L12+T3] 角动量和自旋方面:角动量算子。斯特恩-格拉赫实验 - 自旋。氢原子问题的解。 [L10+T4] 量子信息简介:量子密码学、纠缠、量子计算、EPR悖论、贝尔不等式 [L8+T2]