XiaoMi-AI文件搜索系统
World File Search System浆果
Bloch状态的浆果曲率
Quantum Hall效应首先是由Klitzing等人意外发现的。，1980年在2deg。此后在二维材料（例如石墨烯和WSE 2（过渡金属二甲基化）等材料中观察到了它。为了拥有QHE或QAHE，系统必须是二维的，因为拓扑Chern数仅在偶数上定义。另外，需要通过磁场或磁化而打破时反转对称性。最后，必须有一个完全填充的非零Chern数的能量带。在实践中，我们通常需要一个低温的环境，以避免在能量间隙上进行热激发，并具有高磁场以扩大能量隙（再次避免进行热启动）。如果间隙能量比热能大得多，则可能具有室温QHE（Novoselov等人。，2007年）。
浆果植物保护指南 2025–26
新南威尔士州 DPIRD 免责声明 本出版物中包含的信息基于撰写时（2025 年 1 月）的知识和理解，可能不准确、不最新或不完整。新南威尔士州（包括初级产业和区域发展部）、作者和出版商对文件中包含的任何信息（包括第三方提供的材料）的准确性、时效性、可靠性或正确性不承担任何责任。读者在做出与本出版物中包含的材料相关的决定时，应自行查询并依靠自己的建议。本出版物中的产品商品名是基于以下理解提供的：不打算在等效产品之间进行偏好，并且产品名称的包含并不意味着该部门对其他制造商的任何等效产品的认可。认识到本文件中的部分信息由第三方提供，新南威尔士州、作者和出版商对第三方提供的文件中包含的任何信息的准确性、时效性、可靠性和正确性不承担任何责任。
超级食物浆果鳄梨免疫碗
每份营养事实：卡路里：300 |总脂肪：13 g |饱和脂肪：1.5 g钠：50 mg |总碳水化合物：44 g |饮食纤维：12 g |蛋白质：8 g适应|今天爱一个食谱，请访问www.nutrition.va.gov
在极端潮湿的天气中管理浆果
免责声明本出版物中包含的信息基于写作时的知识和理解（2025年2月），可能不准确，当前或完整。新南威尔士州（包括初级产业和区域发展部），作者和出版商不承担任何责任，并且对文档中包含的任何信息的准确性，货币，可靠性或正确性（包括第三方提供的材料）不承担任何责任。读者应在做出与本出版物中包含的材料有关的决策时进行自己的询问，并依靠自己的建议。
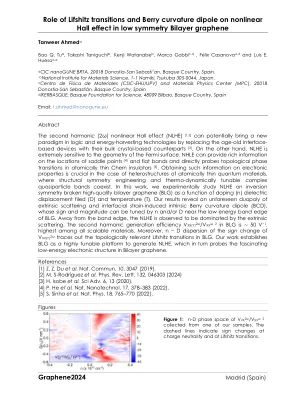
Lifshitz过渡和浆果曲率偶极子在非线性的作用
第二次谐波（2Ω）非线性霍尔效应（NLHE）[1,2]可以通过用基于大的基于晶体的同类产品代替古老的基于界面的设备，从而带来逻辑和能量收获技术的新范式[3]。另一方面，NLHE对费米表面的几何形状非常敏感。nhle可以在鞍点[4]和扁平带的位置提供丰富的信息，并直接探测原子上薄的Chern绝缘子中的拓扑相变[5]。在原子薄量子材料的异质结构中获取有关电子特性的信息至关重要，那里的结构对称性工程和热功能可调的复杂的准粒子带共存。在这项工作中，我们在反转对称性的高质量双层石墨烯（BLG）上进行了实验研究，这是掺杂（n）介电位移的函数（d）和温度（t）。我们的结果揭示了不可预见的外在散射和界面应变诱导的内在浆果曲率偶极子（BCD）的二二，其符号和幅度可以通过N和/或D在BLG的低能带边缘附近调节。远离带边缘，观察到NLHE由外部散射占主导地位。BLG中的第二个谐波产生效率V XX（Y）2Ω /VXXΩ2为〜50 V -1，在所有可伸缩材料中最高。此外，v xx（y）2Ω的符号变化的n -d分散轨迹轨迹在BLG中带走了与拓扑相关的LIFSHITTINTIONS。我们的工作将BLG建立为一个高度可调的平台，以生成NLHE，进而探测双层石墨烯中引人入胜的低能电子结构。
将超导性的浆果相模型与基于TGD的模型进行比较
2基于TGD的超导性模型6 2.1基于TGD模型的简要摘要。。。。。。。。。。。。。。。。。。。。。。。。。。6 2.1.1 TGD框架中超导性的一般机制。。。。。。。。6 2.1.2高t C SC和Bio-SC的定量模型。。。。。。。。。。。。。。。。。7 2.2集体阶段的TGD对应物，新型磁场和Berry的阶段8 2.2.1 Beltrami流量作为非疾病流动的时空相关。。。。。。。。8 2.2.2所有保守的电流都可以定义可集成的流吗？。。。。。。。。。。。。。10 2.2.3一些示例。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。10 2.2.4 Khler的M 4部分是否形成问题？。。。。。。。。。。。。。11 2.3连贯的状态和费米数编号保护的问题。。。。。。。。11 2.3.1琼脂化需要有效的1+1维。。。。。。。。。。。。。。12 2.3.2与照球体相关的KAC-MOODY对称性。。。。。。。。。。。13 2.3.3琼脂化需要Beltrami属性。。。。。。。。。。。。。。。。。。。。14 2.3.4为什么库珀对的形成是形成h eff> h黑暗相位的？。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。14 2.4有效的哈密顿官的一般形式。。。。。。。。。。。。。。。。。。。。。14 2.5从BCS理论开始，更精确地表达了基于TGD的理论。。15 2.5.1临界温度作为磁性弹力管的Hagedorn温度。。。15 2.5.2基于差距能量的解释。。。。。。。。。。。。。。。。。。16 2.5.3单子频磁场和h eff的值是多少？。。17 2.5.4基于Josephson效果的基于TGD的模型。。。。。。。。。。。。。。。。。。。。。19
手学激发型过渡中的浆果曲率特征
引入的电子传输和定期有序固体中的动力学由内在的量子机械性能，例如电子带结构以及电子，声子和其他准粒子之间的相互作用。Bloch波函数的量子几何形式表现为浆果曲率（反映了Bloch电子的惯性），带状质量，Fermi-liquid Transperties（1），Current-Noise-Noise noise noise noise noise targuin-istics（2），或在平面系统（3）中的超级效果（3），这些数字（3）的数量（3），这些基金会（3），这些基金会（3），这些基金会均具有这些资格。更一般地，Bloch电子的量子几何形状非常重要，因为它为量子力学和材料的电子特性之间的复杂相互作用提供了关键的见解。最近，量子几何形状与光 - 物质相互作用之间的联系已进入舞台，从而提供了对拓扑材料的特殊光电子响应的物理机制的见解（4-8）。然而，Bloch Electrons量子几何形状的动量分辨测量仍然是一个巨大的挑战。在冷原子的背景下引入了一种直接的方法，利用了量子几何形状和光结合相互作用之间的紧密联系，在该环境中，可以直接实现范式模型系统。因为带间过渡偶极基矩阵元素等效于浆果连接（9），所以在谐振单色
非线性对变形的Jaynes – Cummings模型的浆果相和热纠缠的影响
摘要。变形Jaynes – Cummings模型（JCM）在量子光学元件中具有物理重要性。因此，我们研究了非线性JCM，包括强度依赖性耦合常数和额外的KERR项。在温度t处，假定腔体在热平衡中，并具有热储存液。使用封闭的代数的发电机在限制情况下还原为SU（1，1）和Heisenberg – Weyl代数，并考虑总兴奋数为运动常数，Hilbert Space的总Hilbert Space分解为两个子空间。因此获得了特征值和相应的特征向量。我们得出了热密度矩阵，并使用消极措施分析了实现和热纠缠。此外，我们研究了非线性原子 - 场系统的浆果相，并探讨了非线性对量子相变（QPT）点和纠缠的影响。发现变形参数可以强烈影响实现，负性和QPT点。