XiaoMi-AI文件搜索系统
World File Search System混合态
通过激光脉冲和衰变的相应驱动实现量子相干性
其中 T 是时间排序算子。虽然 U(t2,t1) 的显式计算极其困难，但显然时间相关哈密顿量引起的动力学将 t1 时的量子态双射映射到 t2 时的量子态，并保持相互的标量积。因此，如果系统最初处于高熵 S>0 的混合态，它将永远保持混合态，且熵完全相同。即使对 H(t) 在时间上的完全理想控制，也无法以这种方式产生相干性。因此，必须考虑开放系统。生成单一状态的标准方法是使感兴趣的系统与冷系统进行热接触。一般来说，这是一个极其缓慢的过程。目标量子态必须是某个给定系统的基态。另外，一般的光泵浦和特别是激光冷却 [1] 都是利用共振泵浦和自发衰变来降低微观系统熵的成熟技术。最近，工程耗散已被认为是在小型 [2-4] 和扩展系统 [5,6] 中产生目标纠缠量子态的一种手段。实验上，已经证明了两个量子比特 [7,8] 和两个捕获的中观铯云 [9] 存在纠缠。在本文中，我们表明，如果涉及中间、高度激发和衰减态，周期性驱动可以使量子系统收敛到相干量子态。关键方面是泵浦脉冲周期与内部过程的时间常数（这里是拉莫尔进动）的可比性。这将我们的提议与已建立的光泵浦协议区分开来。完全无序的初始混合物可以变得几乎相干。最终混合物的熵仅为 S ≈ kB ln2，对应于两种状态的混合。一个吸引人的优点是，一旦关闭驱动，林德布拉衰变就不再重要，系统仅受哈密顿动力学支配。本研究的重点是通过示范性方式展示在周期性激光脉冲作用下小自旋系统中熵的大幅降低。选择该系统的动机是量子点中电子自旋与核自旋相互作用的实验[10-17]。所研究的模型也适用于分子自由基中的电子自旋[18]或分子磁体，见参考文献[19-21]。在有机分子中，自旋浴由有机配体中氢原子核的核自旋决定。
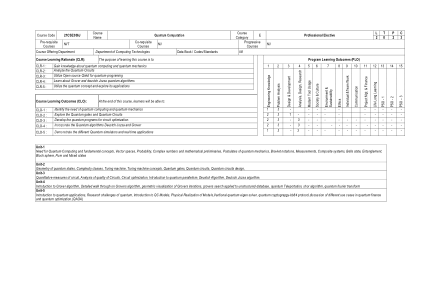
课程代码 21CSE306J 课程名称 量子...
单元 1 量子计算需求和基本概念、向量空间、概率、复数和数学预备知识、量子力学假设、Bra-ket 符号、测量、复合系统、贝尔态、纠缠、布洛赫球、纯态和混合态 单元 2 量子态的几何形状、复杂性类、图灵机、图灵机概念、量子门、量子电路、量子电路设计 单元 3 电路的定量测量、电路质量分析、电路优化、量子并行性简介、Deustch 算法、Deutsch Jozsa 算法 单元 4 Grover 算法简介、Grovers 算法详细介绍、Grovers 迭代的几何可视化、Grovers 搜索应用于非结构化数据库、量子隐形传态、Shor 算法、量子傅里叶变换 单元 5 量子应用简介、量子研究挑战、QC 模型简介、模型的物理实现、变分量子特征求解器、量子密码学-bb84协议，讨论量子金融和量子优化中的不同用例。（QAOA）
![arXiv:2104.05238v1 [math-ph] 2021 年 4 月 12 日](/simg/8\8b924950f0f29a30c4593bb7313488328af01b08.webp)
arXiv:2104.05238v1 [math-ph] 2021 年 4 月 12 日
近年来，由于实验技术的进步，量子通信的实际应用，即利用基本粒子的量子态进行信息编码传输，迈向了一个新的发展阶段[1–3]。结果表明，超选择现象在量子信息传输研究中起着重要作用[4, 5]。自然界中，只可能发生对应于电荷超选择算符的同一特征值的态的相干叠加，而超选择规则[6]禁止发生对应于其不同值的叠加态。不同区域的任何纯态叠加都会导致密度矩阵描述的混合态。在论文[7]中，我们提出了一个代数模型，用于研究具有非阿贝尔超选择规则的少核子系统。本文的目的是利用该模型描述在非阿贝尔同位旋超选择规则存在的情况下，借助核子进行的量子信息传输。
![arXiv:2211.00623v1 [quant-ph] 2022 年 11 月 1 日](/simg/e\e4783ce84404e42510c1692fb56a4039487239ab.webp)
arXiv:2211.00623v1 [quant-ph] 2022 年 11 月 1 日
我们证明，J 1 − J 2 海森堡量子自旋链的基态和第一激发态混合态（相邻态）中的最近邻纠缠可用作序参量，检测链从无间隙自旋流体到有间隙二聚体相的相变。我们研究了序参量对于不同系统尺寸下相邻态中基态和第一激发态之间相对混合概率变化的有效性，并将结果外推到热力学极限。我们观察到，即使系统处于基态，但有较小且有限的概率泄漏到第一激发态，最近邻纠缠也能起到良好序参量的作用。此外，我们应用相邻态的序参量研究了在模型相图上分别引入各向异性和玻璃无序时的响应，并分析了相应的有限尺寸尺度指数和前一种情况下出现的三临界点。各向异性的 J 1 − J 2 链具有更丰富的相图，使用相同的序参量也可以清楚地看到。
一维和二维的实时动态...
量子模拟器中的最新实验为多体局域 (MBL) 相在单维 (1D) 和二维 (2D) 玻色子量子物质中的存在提供了证据。然而，由于其希尔伯特空间的无界性质，对这种玻色子 MBL 相的理论研究是一项艰巨的任务。在这项工作中，我们介绍了一种方法来计算强无序和弱相互作用下 MBL 相中 1D 和 2D 玻色子系统的长期实时演化。我们专注于能够区分 MBL 相和 Anderson 局域相的局部动力学指标。特别是，我们考虑了局部可观测量的时间涨落、双时间相关器和非时间相关器的时空行为。我们表明，通过扩展最近提出的数值方法 [G. De Tomasi、F. Pollmann 和 M. Heyl，Phys. Rev. B 99，241114(R) (2019) ] 到混合态和玻色子。我们的方法还允许我们用对所研究量随时间变化行为的分析考虑来替代我们的数值研究。
从量子信息到黑洞再到量子计算的复杂性
摘要 量子计算复杂度估计了从基本操作构建量子态的难度，这是量子计算中最重要的问题。令人惊讶的是，这个量也可以用来研究一个完全不同的物理问题——黑洞内部的信息处理。量子计算复杂度被建议作为全息词典中的一个新条目，它扩展了几何和信息之间的联系，并解决了黑洞内部为什么会长时间增长的难题。在这篇教学评论中，我们介绍了尼尔森倡导的几何复杂性方法，并展示了如何使用它来定义一般量子系统的复杂性；特别是，我们关注 QFT 中的高斯态（纯态和混合态）以及某些类的 CFT 态。然后，我们提出了全息对应中与引力量的推测关系，并讨论了几个测试了不同版本猜想的例子。我们强调了混沌系统中的复杂性、混沌和混乱之间的关系。最后，我们讨论了未解决的问题和未来发展方向。本文是为 EPJ-C Frontiers in Holographic Duality 特刊撰写的。
TAVAKOLI，Armin 等人。量子理论中的上下文相关性的界限和模拟。在：PRX quantum，2021 年，第 2 卷，第 2 期，第 020334 页。doi：10.1103
我们在广义语境场景中引入了一组量子关联半定松弛层次。这构成了一个简单而通用的工具，用于限制量子语境的量级。为了说明它的实用性，我们用它来确定几个非语境不等式的最大量子违反，这些不等式的最大违反程度以前是未知的。然后，我们进一步用它来证明某些准备语境关联不能用纯态来解释，从而表明混合态是语境不可或缺的资源。在本文的第二部分，我们将注意力转向一般操作理论中准备语境关联的模拟。我们引入了模拟准备语境的信息成本，它量化了模拟经典或量子模型中的语境关联所需的额外信息（否则是被禁止的）。在这两种情况下，我们都证明了使用半定松弛层次的变体可以有效地限制模拟成本，并且我们在最简单的奇偶校验无关复用上下文场景中精确计算它。
量子能量隐形传态中量子关联的稳健性
在本文中，我们探索了不同量子场论 (QFT) 中的反馈控制协议，以研究量子系统非幺正演化中的量子关联。传统的 QFT 研究侧重于幺正演化下纯态的量子纠缠，然而，我们使用量子能量隐形传态 (QET)（一种利用基态纠缠的能量传输协议）来研究混合态中的量子关联，并引入量子不和谐作为度量。QET 涉及中间电路测量，这会破坏纯态纠缠。尽管如此，我们的分析表明，量子不和谐在整个 QET 过程中保持关联。我们使用包括 Nambu-Jona-Lasinio (NJL) 模型在内的基准模型进行了数值分析，揭示了量子不和谐始终充当相变的序参数。该模型被扩展为同时具有手性化学势和化学势，这对于研究模拟与手性密度算子耦合的左夸克和右夸克之间的手性不平衡的相结构很有用。在我们研究的所有情况下，量子不和谐都表现为相变的序参数。
从量子信息到黑洞
摘要 量子计算复杂度估计了从基本操作构建量子态的难度，这是量子计算中最重要的问题。令人惊讶的是，这个量也可以用来研究一个完全不同的物理问题——黑洞内部的信息处理。量子计算复杂度被建议作为全息词典中的一个新条目，它扩展了几何和信息之间的联系，并解决了黑洞内部为什么会长时间增长的难题。在这篇教学评论中，我们介绍了尼尔森倡导的几何复杂性方法，并展示了如何使用它来定义一般量子系统的复杂性；特别是，我们关注 QFT 中的高斯态（纯态和混合态）以及某些类的 CFT 态。然后，我们提出了全息对应中与引力量的推测关系，并讨论了几个测试了不同版本猜想的例子。我们强调了混沌系统中的复杂性、混沌和混乱之间的关系。最后，我们讨论了未解决的问题和未来发展方向。本文是为 EPJ-C Frontiers in Holographic Duality 特刊撰写的。
关联玻色子量子场多模态的纠缠和光学非经典性
有几种方法可以质疑物理系统状态的具体量子力学特性。首先，人们可能会问它的相干性有多强。量子态相干叠加的存在是物质波干涉现象的起源，因此，这是一个典型的量子特征，对此提出了几种测量和证据（有关最近的综述，请参阅 [1]）。其次，当所研究的系统是二分或多分系统时，其组成部分的纠缠是另一个内在的量子特征。有大量文献探讨了各种测量方法来量化给定状态中包含的纠缠量 [2–14]。最后，对于玻色子量子场的模式，出现了第三种非经典性概念，通常称为光学非经典性。根据格劳伯的观点，光场的相干态（及其混合态）被视为“经典”，因为它们具有正的格劳伯-苏达山 P 函数 [15]。从那时起，多年来人们开发了多种光学非经典性测量方法，以测量与光学经典状态的偏离 [15–41]。光场量子态的这三种不同的、典型的量子属性被认为可作为量子信息或计量学的资源 [38, 39, 42–44]。那么自然而然地就会出现一个问题：这些属性之间有着什么样的定量关系。例如，在 [45] 中，给出了使用非相干操作从具有给定相干度的状态中可以产生多少纠缠的界限：这将相干性与纠缠联系起来。在 [46] 中，状态的相干性和光学非经典性被证明是相互关联的：远对角线密度矩阵元素 ρ ( x, x ′ ) 或 ρ ( p, p ′ ) 的显著值（称为“相干性”）是状态的光学非经典性的见证。我们的目的是建立多模玻色子场的光学非经典性和二分纠缠之间的关系。直观地看，由于所有光学经典态都是可分离的，因此强纠缠态应该是强光学非经典态。相反，仅具有弱光学非经典性的状态不可能高度纠缠。为了使这些陈述精确且定量，我们需要测量纠缠度和光学非经典性。作为评估二分纠缠的自然指标，我们使用形成纠缠 (EoF) [4]。关于光学非经典性，我们使用最近引入的单调性 [38, 39]，我们将其称为总噪声单调性 ( M TN )。它是通过将纯态上定义的所谓总噪声∆x2+∆p2扩展到混合态（通过凸屋顶结构，参见(1)）得到的，对于该值来说，它是光学非经典性的一个完善的量度[38–41]。我们的第一个主要结果（定理 1 和 1'）在于，对于 n = n A + n B 模式的二分系统的任意状态 ρ，EoF(ρ) 关于 M TN (ρ) 的函数有一个上限。特别地，当 n A = n B = n/ 2 时，这个上限意味着包含 m 个纠缠比特的状态必须具有光学非经典性（通过 M TN 测量），并且该光学非经典性随 m 呈指数增长。作为应用，我们表明，当可分离纯态撞击平衡光束分束器时可以产生的最大纠缠度由该状态的光学非经典性的对数所限制，通过 M TN 测量。换句话说，虽然众所周知分束器可以产生纠缠 [28, 47, 48]，但纠缠量受到本态光学非经典性程度的严重限制。定理 1 和 1' 中的界限可以很容易地计算出纯态的界限，因为 EoF 与还原态的冯·诺依曼熵相重合，而 M TN 与总噪声相重合。然而，对于混合态，界限与两个通常难以评估的量有关。我们的第二个主要结果（定理 2）解决了这个问题