XiaoMi-AI文件搜索系统
World File Search System回顾联邦调查局对布兰登·马夫菲尔德案的处理
ii. FBI 实验室 LPU 潜指纹检查流程概述 ...................................................................................... 97 A. 管理 LPU 的政策和程序 .............................................................................. 97 B. 摩擦脊和指纹识别的前提 ...................................................................... 98 J C. 潜指纹 ............................................................................................. 99 D. 已知或样本指纹 ............................................................................. 104 E. 用于潜指纹识别的 AC EV 流程 ............................................................. 105 1. 分析 ............................................................................................. 105 2. 比较 ............................................................................................. 107 3. 评估 ............................................................................................. 109 a. 个别化(识别) ............................................................................. 109 b. 排除 ............................................................................................. 112 c.不确定 113 4. 验证 ................................................................................................ 115 F. 宣布匹配的标准 ................................................................................ 116 G. 集成自动指纹识别系统 (IAFIS) ........................................................................................ 118 H. 同时印模 ................................................................................................ 121 I. 文件和审查要求 ...................................................................................... 122 J. 错误 ............................................................................................................. 123
arXiv:2208.01297v2 [nucl-th] 2022 年 10 月 29 日
我们研究了在√sNN≈3.0-30GeV中心区Au+Au碰撞中Λ定向流对Λ势的敏感性。由手性有效场理论(χEFT)获得的Λ势用于微观传输模型,该模型是相对论量子分子动力学的矢量版本。我们发现,由χEFT获得的密度相关Λ势(假设势的动量依赖性较弱)重现了STAR合作在束流能量扫描程序中测得的Λ定向流的快速性和束流能量依赖性。虽然Λ定向流对势的密度依赖性不敏感,但它易受动量依赖性的影响。我们还表明,基于冲击波模型的流体动力学图预测质子、Λ 和 Ξ 定向流的相似性,但 Ω 重子的定向流与其他重子略有不同。我们还表明,夸克聚结预测超子的定向流具有不同的快度依赖性。这些研究表明,对超子定向流快度依赖性的广泛测量可能为高能重离子碰撞中产生的热致密物质的性质提供重要信息。
超对称量子力学
超对称是玻色子和费米子之间的一种理论对称,它为标准模型中的一些问题提供了令人满意的解决方案。目前还没有实验表明它的存在。超对称量子力学 (SUSY QM) 最初是在破缺超对称的背景下研究的,作为量子场论测试方法的环境。SUSY QM 很快成为一个独立的研究领域,除了测试超对称破缺之外,还发现了它的几种应用。本文介绍了超对称量子力学。推导了主要公式,并讨论了作为玻色子-费米子对称的数学形式主义的解释。研究了上述两个应用,即形状不变势和准可解系统。研究发现,SUSY QM 提供了一种对势进行分类和求解的简洁方法,势是一种与形状不变性相关的属性。两个已知的可解势被证明是形状不变的。此外,还展示了如何使用 SUSY QM 来解决和寻找新的准可解势。最后,以这两个应用作为激励示例,论证了研究超对称量子力学的动机。
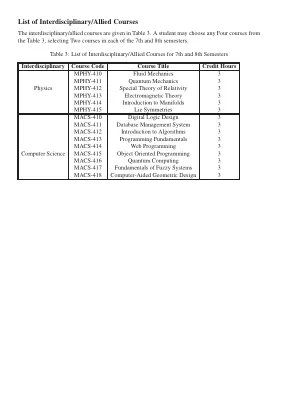
跨学科/相关课程列表
静磁场:磁静力定律、磁感应、磁场中运动的点电荷所受的洛伦兹力、磁场的发散、矢势、电荷守恒和连续性方程、洛伦兹条件、磁场的旋度、安培定律和标量势。
根得高新材料(浙江)有限公司
This dootmentis an authentic electronic certiticate for.CIienr business purposes use only.Printed version of the electronic cerliticate are permitted and will 昙乡遨里 瞥卿 stoerea 竺气 copy.I nis 000iment is 笋 uec Dy 哄 uompa,su 瞥件. to 钟‘ ene 卿 t 只 1aIuons or ceruscaP 甲 servi 毕 avaiiaoie 叭 terms 即 U uonamons !势“溉 AttenoOflis, ,照 me 少 mi"non or 少恻咚 inaemnii 卿 on'ano junsoicuonai ,只 auses con 哪叩吧 Ffl.I fliS aoatmern is copyngnt 涤弓绮溉 prowct 加 ana any unauuionz 印 aiwrat 狱 1,0'ery or 曰巧 In 口 soil or me 以 xuentorap 祀 aranc 刀 01 川石 uoajmern IS Uflidw'UI.
量子自洽运动方程法用于在量子计算机上计算分子激发能、电离势和电子亲和力
为了估计嘈杂的中尺度量子 (NISQ) 时代设备上的分子基态特性,基于变分量子特征求解器 (VQE) 的算法因其相对较低的电路深度和对噪声的抵抗力而广受欢迎。9,10 这导致了一系列成功的演示,涉及在当今的量子设备和模拟器上计算小分子的分子基态能量。4,6,11 – 22 然而,仅仅估计分子基态能量不足以描述许多涉及某种形式的电子激发的有趣化学过程。23 例如,准确模拟化学现象,如光化学反应、涉及过渡金属配合物的催化过程、光合作用、太阳能电池操作等,需要准确模拟分子基态和激发态。此类系统的电子激发态通常具有很强的相关性,因此需要使用复杂的量子化学理论来准确描述它们。在过去的几十年里,在这方面已经开发了许多方法。 24 – 32 运动方程耦合团簇 (EOM-CC) 26 方法最初由 Stanton 和 Bartlett 开发,是一种常用的例子,通常用于计算分子激发态特性,例如激发能
用机器学习的原子势来加速无机表面的预测Kyle Noordhoek 1,Christopher J. Bartel 1 * 1离开
固态材料的表面特性通常决定其功能,尤其是对于纳米级效应变得重要的应用。相关表面及其性质在很大程度上是通过材料的合成或操作条件来确定的。这些条件决定了热力学驱动力和动力学速率,负责产生观察到的表面结构和形态。计算表面科学方法长期以来一直应用于将热化学条件与表面相稳定性联系起来,尤其是在异质催化和薄膜生长群落中。本综述在引入新兴数据驱动的方法之前对第一原理的方法进行了简要介绍,以计算表面相图。其余评论的重点是机器学习的应用,主要是以学识的间势的形式来研究复杂的表面。随着机器学习算法和训练它们的大型数据集在材料科学中变得越来越普遍,计算方法有望变得更加预测性和强大,以建模纳米级的无机表面的复杂性。简介
构型步进限制实现了可调手性的近红外发光超分子势噻嗪有机框架
在此报告,报告了从三肽到Achiral网络超分子有机框架(SOF)的手性转移,基于构造式踩踏置构,它不仅显示了高度选择性的可逆性刺耳性转移(还显示出近来的nir nir nir cornir cornir cornir cornir cornir cornir cornir nir nir nir nir nir,Taking advantage of macrocyclic confinement, CB[8] separately encapsulated two kinds of tetracationic bis(phenothiazines) derivatives (G1, G2) at 2:1 stoichiometric to form organic 2D SOFs, efficiently enhancing 12.6 fold NIR luminescence and blueshifted from 705 to 680 nm for G1, and redshifted G2分别为695至710 nm。毫不偶然地,三种肽与两种非毒剂非共价框架(G1/CB [8]或G2/CB [8])表现出不同的圆二色性信号,其基于不同的结合模式和效果的奇异式旋转模式,并取得了良好的chirition contrirect and y ryflative contrirative trapprAMECTRAMEC,在G2/CB的量度最多46.2倍,量子产率(QY)从0.71%增加到10.29%[8],显示可逆性的手性转移和在热刺激下可调的NIR荧光。因此,当前的研究已实现了从三肽到SOF的可控手性转移,并增强了可调的NIR荧光的能力,后者成功地应用于热反应性手性手性逻辑门,信息加密和细胞成像中。
通过量子系统参数估计增强随机过程分析
摘要 本文从所有可能的角度研究了向量空间中的线性伊藤随机微分方程。在这种情况下,势向量描述了作用于量子系统的经典噪声的大小。该向量势可以表示为其参数的线性函数,其中厄米算子作为其系数,因为其参数被假定为未知的。对于二阶扰动,可以借助势扰动参数确定幺正演化算子。至于第二项,它写成关于布朗运动的双迭代随机积分,而第一项写成伊藤随机积分。在控制量子系统时,来自环境的噪声可能是一个主要障碍;这种技术可以提供帮助。通过学习检测和调节噪声,提高计算机等量子技术的可靠性和实用性。如果势的参数受到噪声的影响,那么它们的可靠性就会降低。我们重点关注特殊情况,即势能是这些参数的线性函数,以厄米算子为系数。为了找到达到 O ( ǫ ) 的幺正演化算子,我们可以将 O ( ǫ ) 项写为关于布朗运动的伊藤随机积分,将 O ( ǫ 2 ) 项写为关于布朗运动的双迭代随机积分。
薛定谔方程的量子模拟
量子计算是物理学研究中最有前途的活跃领域之一。这是因为量子算法有潜力超越经典算法。与经典线性搜索相比,Grover 搜索算法的速度提高了二次方。与经典模拟相比,薛定谔方程的量子模拟具有指数级的内存节省。本文回顾了量子计算的思想和工具。以 Grover 算法为例进行了研究和模拟。使用 Qiskit 量子计算库,开发了一个模拟一维粒子薛定谔方程的代码,在本地进行模拟,并在实际的 IBM 量子计算机上运行。在零势场、谐波势场和线性势场中演化出几个初始状态。将得到的结果与文献中的类似结果进行了比较。


![arXiv:2208.01297v2 [nucl-th] 2022 年 10 月 29 日](/simg/e\e9442ff7e07ee4030cbda0a8eff22afdd5360c5f.webp)