XiaoMi-AI文件搜索系统
World File Search System顶夸克对量子力学对撞机试验中的局域性
高能对撞机中基本粒子量子特性的测试开始出现。顶夸克和反顶夸克系统中的纠缠和贝尔不等式违反尤其令人感兴趣,因为顶夸克是经历级联衰变的不稳定粒子。我们争论顶夸克和反顶夸克在不同衰变阶段的空间分离标准。我们考虑了三个不同情况下的因果分离:顶夸克衰变、W 玻色子衰变以及轻子/喷流与宏观仪器接触时。我们表明,当要求顶夸克和 W 玻色子都在空间间隔内衰变时,事件的空间分数最小。对于通常需要贝尔不等式违反的高不变质量,这几乎与顶夸克衰变要求相同。我们还包括一个选项,用于将顶夸克衰变中的 b 夸克的角度相关性用于自旋相关性测量。我们要求顶夸克和 b 强子衰变都是空间分离的。再次,我们发现在高不变质量下,它几乎与顶夸克和反顶夸克之间的空间分离要求相同。我们为我们提出的标准提供了数值。如果满足这样的标准,则保证系统不存在因果关系。
分数统计
粒子组件的量子力学描述仅限于两个(或一个)空间尺寸的粒子的组件,提供了许多与玻色子和费米子不同的可能性。我们称之为这样的粒子。最简单的Anyons通过角相参数θ进行了参数化。θ= 0,π分别对应于玻色子和费米子。在Intermedi-Ate值中,我们说我们具有分数统计数据。在二维中,θ将波函数获取的相描述为两个逆时针旋转的彼此缠绕。它为相对角动量产生允许值的变化。与Abelian U(1)量规组相关的局部电荷和磁通量的复合材料实现了这种行为。更复杂的电荷升华结构可能涉及在允许的电荷和通量范围内的非亚伯和产品组,从而产生非亚伯和相互统计。nonabelian Anyons的互换在内部状态的新兴空间内实现了波函数的单一转换。各种各样的人都用包括Chern -Simons项在内的量子场理论来描述。环上的一维Anyons的交叉点是单向的,因此互换时获得的分数相θ产生了Anyons之间相对动量的分数移动。最近,在ν= 1/3中的准粒子预测的Anyon行为< / div>
相互作用标量量子场论中相变的量子计算
例如本文研究的量子相变,我们的格模型必须包含大量的位点 L ≫ 1,因此该张量积的因子数量也是 L 。量子计算机为解决这些大型 Fock 空间提供了一种令人鼓舞的方法,因为它们本质上是以量子力学的方式运行的。事实上,目前人们正在大力努力在量子硬件上模拟相对论量子场论。一类特别重要的问题是规范场论的模拟,因为它们在描述基本粒子物理学中起着至关重要的作用。这些理论包含玻色子自由度,因此必须解决相应的无限局部希尔伯特空间。在[1-5]中可以找到一些针对此类问题的理论算法建议,在[6-9]中进行了实际的硬件实现。不幸的是,我们目前可用的设备不仅受到量子比特数量的限制,更重要的是受到量子计算机固有的高噪声水平的限制。虽然利用量子纠错 (QEC) [ 10 – 12 ] 的容错量子计算机将来可能会被证明是可靠的,但目前还无法在近期的量子设备(称为噪声中尺度量子 (NISQ) 硬件)上实现 QEC。根据我们当前的现实,有必要找出能够让我们从现有技术中提取有用信息的技术。例如,可以应用不同形式的“错误缓解”技术来对抗噪声。这些技术目前正在研究中,已经设计出几种方法来解决量子计算机中一些最常见的重大错误源,包括读出(RO)误差[13-16],也称为测量误差,以及由两量子比特门(如受控非(CNOT)门)引起的退相干[17-19]。更直接的解决方案是实现混合量子-经典算法,从而将量子方面降低到适当平衡其优缺点的水平。另一方面,我们将看到存在这样一种情况,其中哈密顿量的基态是可分解的,用于计算量子相变的经典和量子算法都受益于由此产生的简化。经典地,希尔伯特空间的张量积不再是问题,因为这个问题可以在本地解决。在量子方面,纠缠门的数量以及相关耦合的范围都大大减少。这使得量子电路实际上可以在当今的硬件上实现,即使对于较大的晶格尺寸 L 也是如此。在玻色子场论的情况下,还必须考虑无限局部希尔伯特。虽然我们在调用基于量子比特的架构时总是可以截断这个希尔伯特空间,该架构根据离散变量 (DV) 量子计算运行,用玻色子本身来模拟这些玻色子模式可能更自然。这是在连续变量 (CV) 量子计算中实现的。除了能够访问整个希尔伯特空间外,CV 量子计算机还可以利用更耐退相干的光学元件和状态,并可以使用现有技术有效操纵 [20]。与目前的量子比特设备(如超导芯片或离子阱量子计算机)不同,这种设备未来也可以在室温下通过实验实现 [21]。然而,通用量子计算所需的非高斯门的实现目前尚无定论。
环路中的三体纠缠和贝尔非局域性......
摘要 在本文中,我们在具有 CP 破坏相互作用的标准模型背景下,研究了三体 H → γ l ¯ l 衰变(l = e , μ , τ )的量子纠缠特性,该模型位于轻子汤川区。我们的目的是阐明最终光子、轻子和反轻子在相空间中的纠缠分布。这些罕见的希格斯玻色子衰变发生在 1 圈水平,通过计算并发度和研究贝尔非局域性,为研究三体系统中基本相互作用的量子关联提供了独特的机会。此外,我们还探讨了衰变后和自蒸馏现象。多体纠缠测度比二体情况下的纠缠测度具有更丰富的结构,因此在对撞机现象学中值得更多关注。在这一方面,我们分析了这些三体希格斯玻色子衰变的新可观测量,这些可观测量可以扩展到高能范围内的其他多粒子系统。我们发现纠缠在最终粒子之间表现出来,偶尔在特定的运动学配置中达到最大纠缠状态。此外,这些衰变通道对于贝尔非局域性测试很有前景,但这种可观测量中的 CP 效应被轻子质量抑制。
快速推进的量子进化
我们研究快速转发量子演化问题,即某些量子系统的动力学可以用演化时间次线性的门复杂度来模拟。我们提供了一个快速转发的定义,该定义考虑了量子计算模型、诱导演化的汉密尔顿量以及初始状态的属性。我们的定义考虑了一般情况的任何渐近复杂性改进,并用它来演示几个量子系统中的快速转发。特别是,我们表明,一些局部自旋系统(例如那些具有置换不变性的系统)的汉密尔顿量可以使用有效的量子电路转化为块对角形式,可以指数级快速转发。我们还表明,某些类的半正定局部自旋系统(也称为无挫折系统)可以多项式地快速转发,前提是初始状态由足够低能量的子空间支持。最后,我们表明,在一个量子门分别为特定费米子或玻色子算子的指数的模型中,所有二次费米子系统和数值守恒二次玻色子系统都可以指数级快速转发。我们的结果扩展了以前已知可以快速转发的物理汉密尔顿量类别,而不一定需要有效地对角化汉密尔顿量的方法。我们进一步建立了快速转发和精确能量测量之间的联系,这也解释了多项式改进。
Cern Courier 2024年9月/10月
四个加速器在我们的封面图像中拼接在一起的整个欧洲核查所历史的七十年。他们还讲述了粒子物理标准模型的电动扇区的大部分实验故事。质子同步子产生了用于发现中性电流的中微子束。使用超级质子同步子发现W和Z玻色子。大型电子 - 峰值对撞机(LEP)限制了模型。和Higgs玻色子是在大型强子对撞机上发现的,它 - 相当显着 - 现在与Electroweak Precision中的LEP相当于LEP(P29)。接下来会发生什么?随着欧洲粒子物理战略的第三次更新,辩论现在开始认真开始,并邀请您贡献(P7)。早期研究人员有至关重要的作用。此版本的核心专门针对他们对高能物理学未来的13个观点(P46)。在此版本中也是如此:来自CERN的专家回顾未来(p53);接受CERN委员会主席(P63)的采访;从LHC到医学和工业的技术转移(p37);新物理可能会隐藏在希格斯的自我耦合中(p61);晶格QCD表明,MUON G -2中的新物理学比以前希望的少(P21)。德国社区辩论CERN的未来(P22);基本的时间将抗蛋白酶冷却的时间从15小时到8分钟(P8)。
机器学习符合高X相位空间
随着LHC过渡到精确测量机,质子Parton分布函数(PDFS)已成为分析的不确定性的主要来源,例如顶部夸克质量或HIGGS玻色子宽度的测量值。此外,在LHC处探测最有能力的碰撞时,高摩肌分数(High-X)尤其感兴趣。因此,在此制度中理解并有可能减少PDF不确定性至关重要。使用机器学习技术,我们构建了对High-X机制中Gluon PDF敏感的判别,将在将来的PDF拟合中使用。
UKRI 国际战略框架
英国是 CERN 的 12 个创始成员国之一,拥有来自 75 多个国家的 13,000 多名研究人员,他们都在寻求有关宇宙本质的答案。改变生活的重大突破,如万维网、正电子发射断层扫描 (PET) 扫描仪探测器、触摸屏、光纤传感器和超级计算,都是通过 CERN 实验所需的重大技术进步实现的,所有这些都为英国经济做出了贡献。英国科学家参与了 CERN 八项诺贝尔奖中的三项,包括 2013 年因希格斯玻色子研究而获得的诺贝尔物理学奖。iv
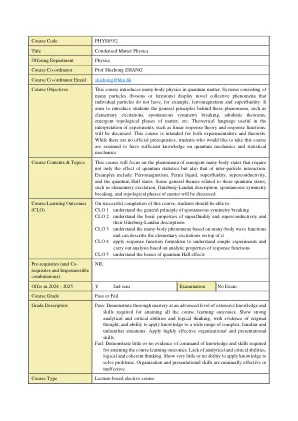
课程代码Phys8552标题缩合物...
课程目标本课程介绍了量子物质中的多体物理学。由许多颗粒(玻色子或费米子)组成的系统显示出新型的集体现象,例如,单个颗粒没有类似铁磁性和超流量。它旨在介绍这些现象背后的一般原则,例如基本激发,自发对称性破坏,绝热定理,物质的新兴拓扑阶段等。将讨论用于解释实验的解释(例如线性响应理论和响应函数)的理论语言。本课程均针对实验者和理论家。尽管没有官方先决条件,但想参加本课程的学生被认为对量子力学和统计力学有足够的知识。
非阿贝尔费米子化和量子霍尔相的景观
最近提出的 2 + 1 维非阿贝尔玻色子-费米子对偶在道义上将 U ( k ) N 与 SU ( N ) − k 陈-西蒙斯物质理论联系起来,为探索从阿贝尔复合粒子理论可获得的非阿贝尔量子霍尔态前景提供了一个新平台。在这里,我们重点研究将玻色子或费米子的阿贝尔量子霍尔态理论与部分填充朗道能级的非阿贝尔“复合费米子”理论联系起来的对偶。我们表明,这些对偶预测了特殊的填充分数,其中阿贝尔和非阿贝尔复合费米子理论似乎都能够承载不同的拓扑有序基态,一个是阿贝尔态,另一个是非阿贝尔态,即 U ( k ) 2 Blok-Wen 态。我们认为,这些结果并不与对偶性相冲突,而是表明了意想不到的动力学,其中红外和最低朗道能级极限无法跨对偶性交换。在这种情况下,非阿贝尔拓扑序可能会不稳定,有利于阿贝尔基态,这表明阿贝尔态和非阿贝尔态之间存在相变,该相变很可能是一级相变。我们还将这些构造推广到其他非阿贝尔费米子-费米子对偶性,在此过程中利用对偶性获得了各种成对复合费米子相的新推导,包括反普法夫态。最后,我们描述了在多层结构中,跨 N 层的复合费米子的激子配对如何也能生成具有 U (k)2 拓扑序的 Blok-Wen 态家族。