XiaoMi-AI文件搜索系统
World File Search Systemrarita-schinginger田地的纠缠熵
我们研究了d¼4minkowski时空中自由费米子场理论的纠缠熵的通用对数系数。作为热身,我们通过对D¼2半线的尺寸减小以及随后在晶格上进行数值实时计算来重新审视无质量自旋1 = 2场情况。出乎意料的是,该面积系数差异以径向离散化,但对于由相互信息引起的几何正则化是有限的。所得的通用对数系数 - 11 = 90与文献一致。对于自由质量自旋 - 3 = 2场,Rarita-Schwinger场,我们还对半行进行了尺寸降低。除了省略最低的总角动量模式外,降低的哈密顿量与自旋1 = 2一致。这给出了一个通用对数系数-71 = 90。我们讨论了无应力能量张量的自由高自旋场理论的通用对数系数的物理解释。
在具有速度障碍的大型动作空间中为移动机器人计划移动机器人的蒙特卡洛
动态环境中的抽象运动计划是一项具有挑战性的机器人任务,需要避免碰撞和实时计算。最新的在线方法作为速度障碍(VO)保证安全的本地计划,而基于强化学习或图形离散化的全球计划方法在计算上效率低下或不可证明是碰撞的安全性。在本文中,我们将蒙特卡洛树搜索(MCT)与VO结合起来,以修剪不安全的动作(即相撞速度)。以这种方式,即使在非常大的动作空间(60个动作)中,我们可以进行极少的MCT模拟计划,比使用许多模拟的纯MCT获得更高的累积奖励和更低的计算时间。此外,由于与VO的动作修剪,我们的方法可以保证避免碰撞,而纯MCT则没有。在本文中铺平了在实际机器人和多代理分散运动计划上计划MCT计划的道路。
一种求解电磁问题的新型无网格方法...
讲师:Meisong Tong 级别:中级 时间:2025 年 2 月 9 日下午 4:00 至下午 6:00 太平洋时间(美国和加拿大) 摘要 体积积分方程 (VIE) 对于通过积分方程方法解决非均匀或各向异性电磁 (EM) 问题是必不可少的。VIE 的解决在很大程度上依赖于体积积分域的适当离散化,对于任意形状的几何形状,通常首选四面体离散化。与离散表面域不同,体积域的离散化在实践中可能非常困难,即使对于简单而规则的几何形状,通常也需要特殊的商业软件。为了降低离散体积域的成本,特别是消除传统矩量法 (MoM) 要求的网格一致性约束,我们最近提出了一种新的无网格方法来解决 VIE。该方法基于通过格林高斯定理将体积积分转换为边界或表面积分,此时通过排除包围观测节点的小圆柱体或立方体来正则化积分核。对象所表示的原始积分域也被扩展为围绕对象的圆柱体或立方体域,以方便计算边界积分。小圆柱体或立方体上的奇异积分采用奇异减法技术进行特殊处理。为了说明该方法,给出了几个解决典型电磁问题的数值示例,并可以观察到良好的结果。简历 童梅松分别在中国武汉华中科技大学获得学士和硕士学位,在美国亚利桑那州坦佩亚利桑那州立大学获得博士学位,专业均为电气工程。他目前是德国慕尼黑工业大学高频工程系洪堡教授,同时也是上海同济大学电子科学与技术系主任、特聘教授和微电子学院副院长。他还曾担任美国伊利诺伊大学香槟分校客座教授和香港大学名誉教授。他在同行评审的期刊和会议论文集上发表了 700 多篇论文,并合作撰写了 8 本书或书籍章节。他的研究兴趣包括电磁场理论、天线理论与技术、射频/微波电路和器件的建模与仿真、互连和封装分析、用于成像的逆电磁散射以及计算电磁学。童教授是电磁学会院士、日本学术振兴会 (JSPS) 院士和 USNC/URSI 成员(B 委员会)。他自 2014 年起担任上海分会主席,并于 2018 年担任 SIGHT 委员会主席。他是IEEE天线与传播学会的博士后研究员,曾担任IEEE天线与传播杂志、IEEE天线与传播学报、IEEE组件、封装与制造技术学报、International Journal of Numerical Modeling: Electronic Networks, Devices and Fields、Progress in Electromagnetics Research、Journal of Electromagnetic Waves and Applications等数本国际著名期刊的副主编或客座编辑,并多次担任一些著名国际会议的分会组织者/主席、技术委员会委员/主席、大会主席等职务。2012年获日本京都大学客座教授称号,2013年获香港大学客座教授称号。他指导并指导了国内外多所著名学术期刊的编辑工作。
航空航天工程 - NASA 技术报告服务器
介绍了一种有效计算复杂二维结构上湍流可压缩流的方法。该方法在整个流场中使用完全非结构化的网格,从而能够处理任意复杂的几何形状,并在粘性和非粘性流场区域使用自适应网格划分技术。网格生成基于局部映射 Delaunay 技术,以便在粘性区域生成具有高度拉伸元素的非结构化网格。使用有限元 Navier-Stokes 求解器对流动方程进行离散化,并使用非结构化多重网格算法实现快速收敛到稳态。湍流建模是使用一种廉价的代数模型进行的,该模型可用于非结构化和自适应网格。计算了多元素翼型几何的可压缩湍流解,并与实验数据进行了比较。作者
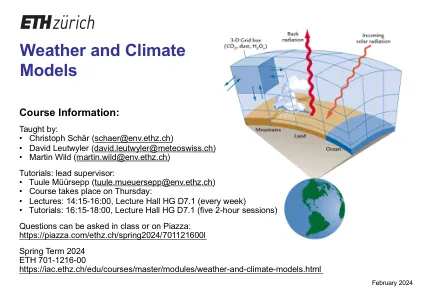
天气和气候模型
教程22.02.2024概述,简介(CS =ChristophSchär)动力学和数字29.02.2024重复数值方法(CS)07.03.2024绝热模型公式:浅水系统(CS)浅水系统(CS)Python Into 14.03.2024 Adiabatic Model 21 21. Vertical 21 21.0.0.0.0.0.0.0.0.0. 0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0.0。公式:水平离散化(CS)教程1物理过程的参数化28.03.2024简介,行星边界层的参数化(MW)教程2 04.04.2024否类别:复活节休息:复活节休息11.04.2024辐射的参数(MW = MARTIN WILD)3 18.04.204.204.204.204.204.204.204.204.204.204. 204. 25. 22. CAMIMIMIMIMIMILATION(C)。大规模云(DL = David Leutwyler)教程4 02.05.2024对流参数(DL)教程5 09.05.2024否类:型号16.05.2024的升天日期应用16.05.2024可预测性,天气和整体预测(CS)23.05.202.05.2024 Earth Systems Models(MW)30.05.05.05.05.05.05.05.2024 Outlook
建造机器人大脑的建议
摘要:现代神经网络已在机器人技术方面取得了重大进展,但是这些算法对时间离散化有了隐含的假设。在本文档中,我们认为,通过设计在连续时间和状态中存在的学习算法,并且后来仅将传统计算模型实施算法离散或直接映射到Analog硬件上,可以获得尤其是在机器人技术中获得的好处。我们调查了支持这种方法的四个论证:连续表示为机器人系统提供了统一的功能理论;该算法以温度连续的形式证明了任何时间属性。我们可以利用时间稀疏性来影响传统和模拟硬件的能量效率;这些算法反映了在生物体中进化的智力的实例。此外,我们提出了从继续表示的学习算法。最后,我们讨论了这种方法的机器人先例,并以在机器人系统中使用连续表示的含义得出结论。
通过混合整数线性规划对工业现场进行综合生产和能源供应规划
摘要:如今,工业生产现场面临两大问题:需要减少生产过程对环境的影响,以及能源价格上涨造成的经济困难。这两个挑战可以通过使用现场可再生能源发电为工业过程提供动力来部分解决。然而,电价的波动性和当地可再生能源的间歇性导致需要解决综合工业生产和能源供应规划问题。这项工作研究了由电网电力和现场可再生能源驱动的工业过程的单机多产品批量问题。我们提出了一种新的比例批量和调度问题扩展,它依赖于两级结构进行时间离散化。第一级与产品需求满足有关,第二级用于生产和能源供应规划。将提出的扩展与之前发布的处理类似问题的一般批量和调度问题扩展进行了比较。我们的初步数值结果表明,在大多数情况下,我们的模型提供了相同成本的生产计划,但计算工作量显著减少。
JHEP11(2024)156
这项工作调查了可符合性(3Þ1) - 二维nambu - Jona-Lasinio(NJL)模型的相结构,特别关注不均匀阶段(IPS),在该阶段(IPS)中,手掌凝结物在空间上是不均匀的,在空间上是不均匀的,密切相关的Moat Moat Companimes,在这里,在这里,有偏见的不合情对离的偏爱不合适的人类关系。我们使用平均场近似值,并考虑五个不同的正则化方案,包括三个晶格离散化。为了研究IP对正则化方案和调节剂价值的选择的依赖性,对不同正则化方案内的结果进行了系统的分析。IP对所选的正则化方案表现出极大的依赖性,该方案在该模型中对不均匀阶段的结果进行了任何物理解释。相比之下,我们发现护城河制度的一个温和的方案依赖性表明其存在是NJL模型及其对称性的作用的结果,因此它也可能存在于QCD中。
旋转超导体有限元模型的螺旋转换方法
摘要 - 本文介绍了具有螺旋形对称性的超导和电阻线的建模,并受到外部场和运输电流的影响。螺旋结构为3-D,因此在笛卡尔坐标系统中产生计算密集型模拟。我们在本文中表明,通过使用坐标系统的螺旋体系统,可以解决要解决的问题,从而大大降低了综合成本。我们首先引入了最新方法,并将其应用于螺旋形的对称边界条件(例如,具有或没有传输电流的轴向外部磁场)的H-φ-构造,重点是功能空间离散化。然后,我们将方法扩展到一般边界条件(例如横向外部磁场),并使用线性材料呈现数值结果。,我们讨论了由嵌入在电阻基质中的超级传导灯泡制成的复合线中的频率损失。最后,我们为使用非线性材料的广义模型提供了前景。
航空航天工程 - NASA 技术报告服务器
介绍了一种有效计算复杂二维结构上湍流可压缩流的方法。该方法在整个流场中使用完全非结构化的网格,从而能够处理任意复杂的几何形状,并在粘性和非粘性流场区域使用自适应网格划分技术。网格生成基于局部映射 Delaunay 技术,以便在粘性区域生成具有高度拉伸元素的非结构化网格。使用有限元 Navier-Stokes 求解器对流动方程进行离散化,并使用非结构化多重网格算法实现快速收敛到稳态。湍流建模是使用一种廉价的代数模型进行的,该模型可用于非结构化和自适应网格。计算了多元素翼型几何的可压缩湍流解,并与实验数据进行了比较。作者