XiaoMi-AI文件搜索系统
World File Search System积分的
ITP-459的教学大纲，第1页
作业提交政策学生负责按规定的截止日期完成个人任务。必须将分配变成Brightspace。迟到的任务将从每3天的晚期分级分数中扣除的总积分的25％。每个学生在整个学期中获得4 x 3天无罚球的日子，除了在决赛周期间，由于成绩提交截止日期。请注意，即使您仅要求延长一天，也将从您的津贴中扣除3天。免费的没有罚款的日子是涵盖所有紧急情况和家庭情况或病假日。在此产品之外没有其他津贴和扩展名。资格是在给课程助理和教授的分配截止日期之前的电子邮件条件。Gen ai案例呈现
不平衡微电网三级控制的凸近似。
本文提出了一种三相不平衡微电网三级控制优化模型。该模型考虑了 24 小时运行，包括可再生能源、储能设备和电网规范限制。使用最近开发的基于 Wirtinger 微积分的近似法简化了功率流方程。对所提出的模型进行了理论和实践评估。从理论角度来看，该模型适用于三级控制，因为它是凸的；因此，保证了全局最优、解的唯一性和内点法的收敛性。从实践角度来看，该模型足够简单，可以在小型单板计算机中实现，计算时间短。后者通过在具有 CIGRE 低压基准的 Raspberry-Pi 板上实现该模型来评估；该模型还在 IEEE 123 节点配电网络测试系统中进行了评估。
本科经济学专业的要求
摘要本文介绍了2019年授予经济学学士学位的793所美国大学的大多数大学的本科经济学课程。除了更新经济学专业的核心要求的普遍性以及这些因素类型如何不同之外，我们还记录了有关经济学学位类型需求变化的新信息，该信息由国家教育统计中心（包括STEM指定学位类型）分类。我们还研究了基于微积分的中级课程的患病率，发现近三分之二（63％）的经济学学位需要计算中级微观经济学和宏观经济学课程。此外，67％的学位需要单变量的微积分，10％需要多变量的计算，而54％的学位需要基本计量经济学（比2010年的41％增加），而这些要求也随度类型而差异很大。
今天在德国进行的负碳除碳
在我们位于巴伐利亚雷姆林根的生物甲烷植物上，我们的开创性解决方案将每年从大气中删除约9,000吨的CO 2。我们将这种解决方案扩展到整个德国的其他植物，为打击气候变化做出了有意义的贡献。在Reimlingen中，另一项创新增强了我们的植物的灵活性：Reverion技术。基于固体氧化物燃料电池的晚期发电厂可将现有的电力转换率翻倍。及其积分的可逆性，它可以在网格中剩余的电力期间通过电解提供氢和合成甲烷。在没有阳光和风的几天里，这种存储的能量尤为重要，因为它可以轻松电气化。我们的联合偿还项目赢得了德国天然气行业可持续生产创新奖。
b.tech. 4 年制电子与通信专业课程...
一元函数微积分：线性和二次近似、误差估计、泰勒定理、无穷级数、收敛测试、绝对和条件收敛、泰勒和麦克劳林级数。多元函数微积分：偏导数、链式法则、隐式微分、梯度、方向导数、全微分、切平面和法线、最大值、最小值和鞍点、约束最大值和最小值、曲线绘制、积分的几何应用、双重积分、面积和体积的应用、变量变换。常微分方程：一阶及高阶微分方程、线性微分方程。具有高阶常数系数、柯西微分方程、参数变异法、联立微分方程。图论：简介、术语、表示、同构、连通性、Wars Hall 算法、欧拉和汉密尔顿路径以及最短路径树。参考文献：
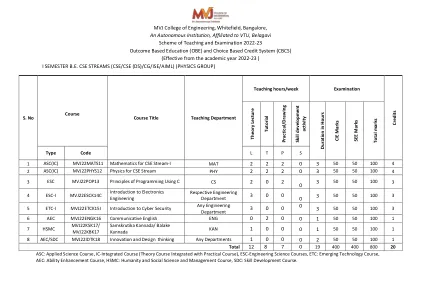
物理循环-CSE-stream-2022-scheme.pdf
•熟悉与一个变量相关的微积分的重要性，并且在计算机科学和工程方面可进行多变量。•通过应用普通微分方程来分析计算机科学和工程问题。•将模块化算术知识应用于计算机算法。•发展线性代数的知识以求解方程系统。模块1 L1，L2和L3 8小时与计算机科学和工程有关的极性坐标和曲率简介。极坐标，极曲线，半径矢量与切线之间的角度以及两条曲线之间的角度。踏板方程。曲率和曲率半径 - 笛卡尔，参数，极性和踏板形式。问题。自学：曲率的中心和圆圈，进化和灭绝。应用：结构设计和路径，材料强度，弹性。模块-2 L1，L2和L3 8小时串联扩展和部分分化的介绍计算机科学领域和
椭圆体的 Minkowski 和与协方差矩阵的均值
摘要。两个椭球集的闵可夫斯基和与差一般不是椭球形的。然而，在许多应用中，需要计算在某种意义上近似闵可夫斯基运算的椭球集。在本研究中，考虑了一种基于所谓椭球微积分的方法，该方法提供了参数化的外部和内部椭球族，可以紧密近似于闵可夫斯基椭球的和与差。近似沿方向 l 是紧密的，因为椭球在 l 上的支撑函数等于和与差在 l 上的支撑函数。然后可以根据相应椭球的体积或迹的最小（或最大）测量值来选择基于外部（或内部）支撑函数的近似。建立了利用欧几里得几何或黎曼几何对两个正定矩阵的闵可夫斯基和与差的基于体积的近似及其均值之间的联系，这也与它们的 Bures-Wasserstein 均值有关。
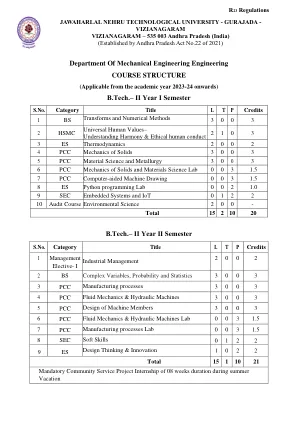
2.Mech-r23-ii.B.Tech syllabus.pdf
单元I：拉普拉斯变换：某些功能的定义和拉普拉斯变换 - 转移定理；衍生物和积分的拉普拉斯转换 - 单位步骤功能 - 迪拉克的dilta函数，周期性函数。反向拉普拉斯转换-Convolution定理（无证明）。应用程序：使用拉普拉斯变换求解普通微分方程（初始值问题）。单元-II：傅立叶级数和傅立叶变换：傅立叶序列：简介，周期功能，一系列周期函数，差异和奇数函数，偶数和奇数功能，间隔的变化，半范围傅立叶正弦和余弦系列。傅立叶变换：傅立叶积分定理（无证明） - 曲线和余弦的正弦和余弦变换 - 跨性别者（文本book-i中的第22.5条） - 逆变换 - 卷积定理（没有证明）有限的傅立叶变换。
艺术状态：CCS Technologies 2024
•我们的氢生产技术没有直接排放，并且达到了超低碳强度，比CCS（ATR+CCS）的最先进的自动热改革低15-20％。•CO 2的捕获固有地内置在过程设计中，捕获超过99.5％，同时避免使用有毒化学物质或能源密集型过程。•结合了商业证明的氢生产过程的优势，以可靠地提供清洁和负担得起的能源。•利用尾巴气体的氧气燃烧来提供改革和热积分的热量，使高效的循环具有5-7％的热效率增益，而基准ATR+CCS。•结合在一起，与目前市场上所有公用事业规模的氢技术相比，8RH 2的平整成本无与伦比。•轻松地与氨循环技术集成，以实现超低碳氨的产生，该氨可以作为商品交易或用于更容易的H 2运输。
![arxiv：2407.20160v3 [physics.optics] 2024年10月30日](/simg/2\2604e6cb2518d42a99c88eb75168a6d779075a26.webp)
arxiv：2407.20160v3 [physics.optics] 2024年10月30日
六角形硝酸硼（HBN）中的颜色中心有利地结合了出色的光物理特性，并具有在高度紧凑的设备中积分的潜力。朝着可扩展集成的进展需要高量子效率和有效的光子收集。在这种情况下，我们比较了在两个不同的电磁环境中由电子辐照产生的单个HBN颜色中心的光学特征。我们跟踪我们在去角质晶体干燥之前和之后表征的良好识别发射器。此比较提供了有关其量子效率的信息 - 我们发现它们接近统一 - 以及它们在晶体中具有纳米精度的垂直位置，我们从薄片表面上发现了它们。我们的工作建议混合介电 - 金属平面结构是一个有效的量子发射器的有效工具，除了提高计数速率外，还可以在2D材料或平面光子结构中推广到其他发射器。