XiaoMi-AI文件搜索系统
World File Search System在温室中与电池储能系统优化透明的光伏整合:考虑贝斯退化的每日光积分受限的经济分析
温室为作物种植提供了控制的环境,并整合半透明的光伏(STPV)面板提供了产生可再生能源的双重好处,同时促进自然光穿透光合作用。这项研究将整合电池存储系统(BESS)与温室农业中的STPV系统进行可行性分析,考虑到不同农作物的每日光积分(DLI)的要求是主要约束。采用增强的萤火虫算法(FA)来优化PV覆盖率和BES的容量,该分析旨在在25年内最大化净现值(NPV),以作为主要经济参数。通过纳入各种农作物类型的DLI要求,该研究可确保最佳的作物生长,同时最大程度地发电。为了确保现实的长期预测,该分析纳入了25年期间的BESS退化,从而考虑了能源储能的容量损失和效率降低。结果揭示了作物类型的重大影响,具有各种必需的DLI和透明度因子对优化的BES,因此对项目的NPV进行了重大影响。仿真结果表明,对于具有较高DLI需求的农作物,温室中的PVR%可行范围从42%到91%,具体取决于STPV的透射因子。此外,该研究表明,在所有情况下,初始负收入都是普遍的,NPV的最高收入为$ 1,331,340,其农作物的需求较低,而BESS容量为216 kW。
B.Sci. (数据科学与人工智能)课程适用于 2018 年或以后入学的学生
MH1802 科学微积分 本课程旨在让学生掌握 数学知识和分析技能,使他们能够应用微积分技术(以及他们现有的数学技能)来解决适用的科学问题; 数学阅读技能,使他们能够阅读和理解基础和流行科学和工程文献中的相关数学内容;以及 数学交流技能,使他们能够有效和严格地向数学家、科学家和工程师介绍他们的数学思想。内容基础 (BAS) 数字类型;函数和图形;常用函数及其图形;重要的代数、三角、对数和指数恒等式;基本复数。微积分 (DIF) 极限;微分;微分技术;微分的应用;基本偏导数。积分 (INT) 积分;积分技术;对数、指数和反三角函数的微积分;积分的应用;微分方程 (DE) 基础;一阶常微分方程;二阶常微分方程;级数、序列和微分方程。MH1812 离散数学 学习目标 本课程介绍数学和计算机科学中常用的离散数学基本概念。内容 - 计数、排列和组合、二项式定理 - 递归关系 - 图、路径和电路、同构 - 树、生成树 - 图算法(例如最短路径、最大流)及其计算复杂度、大 O 符号 MH2100 微积分 III 学习目标 这是微积分系列中的最后一门课程。本课程介绍多变量微积分。内容 参数方程、极坐标。向量值函数、向量值函数微积分、立体解析几何。多变量函数、极限、连续性、偏导数、可微分性和全微分、链式法则、隐函数定理。方向导数、梯度、拉格朗日乘数。二重积分、表面面积、三重积分。线积分、格林定理、曲面积分、高斯散度定理、斯托克斯定理。
夺旗活动规则“传递你的...
- 根据事件的复杂性授予每个事件的积分。游戏平台实时更新排行榜。排名基于积分和速度。如果两支队伍的分数相同,则最快完成所有测试的队伍将获得优势,或者在未能完成所有测试的情况下,最快解决已完成测试的队伍(实际不考虑在平台上花费的时间,但考虑上次测试的完成日期);
贝叶斯推理的计算技术
统计计算很大程度上由概率的加权总和或积分组成。贝叶斯推论和频繁统计之间的关键实际差异之一是,在将这些竞争性的方法解决相同问题的情况下出现了巨大不同类型的积分类型(Loredo 1992)。例如,考虑到某些观察到的数据d,估计某些模型的参数m;用θ共同表示参数。在贝叶斯和频繁的积分中出现的关键数量是假设模型为真的数据并假定要知道的参数的概率,p(d |θ,m)。被认为是数据的函数,这称为采样分布;作为参数的函数,它称为可能性函数,它将缩写为l(θ)。该方法之间的基本实际差异是,频繁计算需要在数据维度(样本空间)上进行此数量的积分,而贝叶斯计算需要在参数空间上进行积分。基于通过参数空间进行求和或集成在试图使用样品空间中计算的概率进行推断的概率的概率上的推断。在这里的简短空间中,对这些优势的重要讨论是不可能的。必须提及两个具有巨大实际实用性的积极优势。在贝叶斯推理中,可以直接消除滋扰参数,同时简单地通过在φ上整合(ψ,φ)的关节分布来解决它们的不确定性。首先,在绝大多数的实际应用中,参数空间可以分为两个部分θ=(ψ,φ),其中兴趣集中在ψ上,并且φ由对数据建模但不感兴趣的“滋扰”参数组成(例如,背景强度)。没有完全的SAT-
通过量子系统参数估计增强随机过程分析
摘要 本文从所有可能的角度研究了向量空间中的线性伊藤随机微分方程。在这种情况下,势向量描述了作用于量子系统的经典噪声的大小。该向量势可以表示为其参数的线性函数,其中厄米算子作为其系数,因为其参数被假定为未知的。对于二阶扰动,可以借助势扰动参数确定幺正演化算子。至于第二项,它写成关于布朗运动的双迭代随机积分,而第一项写成伊藤随机积分。在控制量子系统时,来自环境的噪声可能是一个主要障碍;这种技术可以提供帮助。通过学习检测和调节噪声,提高计算机等量子技术的可靠性和实用性。如果势的参数受到噪声的影响,那么它们的可靠性就会降低。我们重点关注特殊情况,即势能是这些参数的线性函数,以厄米算子为系数。为了找到达到 O ( ǫ ) 的幺正演化算子,我们可以将 O ( ǫ ) 项写为关于布朗运动的伊藤随机积分,将 O ( ǫ 2 ) 项写为关于布朗运动的双迭代随机积分。
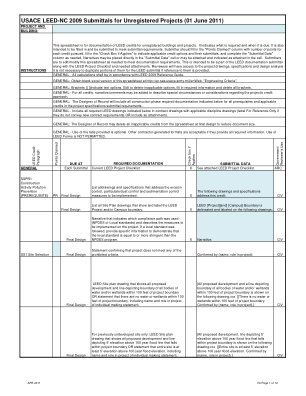
USACE LEED-NC 2009 未注册项目提交
此电子表格用于记录未注册建筑和项目的 LEED 积分。它表明需要什么以及何时到期。它还旨在填写并提交以满足提交要求。提交者应在“已申请积分”列中填写每个积分的积分数,填写“如果适用则勾选”以指示适用的积分选项及其提交,并根据需要完成“提交数据”列。叙述可以直接放在“提交数据”单元格中,也可以附加并在单元格中指示为附加。提交者应根据需要编辑/修改此电子表格以满足文档要求。这旨在与 LEED 项目清单和所需附件一起成为 LEED 文档提交的一部分。审阅者将有权查看项目图纸、规格和设计分析 - 如果提供了参考,则无需在 LEED 提交中复制其中的部分内容。
应用于癫痫发作识别的数据融合方法的性能分析
癫痫是一种由无诱因反复发作引起的慢性神经系统疾病。诊断癫痫最常用的工具是脑电图 (EEG),通过脑电图可以测量大脑的电活动。为了预防潜在风险,必须对患者进行监测,以便尽早发现癫痫发作并采取预防措施。许多不同的研究都结合了时间和频率特征来自动识别癫痫发作。本文比较了两种融合方法。第一种基于集成方法,第二种使用 Choquet 模糊积分方法。具体来说,三种不同的机器学习方法,即 RNN、ML 和 DNN,被用作集成方法和 Choquet 模糊积分融合方法的输入。比较了混淆矩阵、AUC 和准确度等评估指标,并提供了 MSE 和 RMSE。结果表明,Choquet模糊积分融合方法优于集成方法以及其他最先进的分类方法。
240814-02 主题:DD 表格 214 处理提醒...
对于被分配到 AFPC 作为职能类别 X/HQ AGR 或 RegAF 且缺少符合条件的 DD 214 的 ARC 成员,vMPF 中的限制使我们无法处理准确的 DD 214。由于 AFPC 不使用积分,先前现役积分框显示为灰色,我们无法准确记录对福利有直接影响的总服役时间。一旦成员从 AFPC 角色中解脱出来,ARPC 将创建符合条件的 DD 214。