XiaoMi-AI文件搜索系统
World File Search System等价
超越英国脱欧：英国经济的前景
欧盟已授予英国衍生工具的临时等价状态，直到2022年6月底。欧盟还授予了临时等价性，以启用英国中央证券存放者的Euroclear UK＆Ireland，该保存时间为爱尔兰证券提供服务，直到2021年6月底。由于英国脱欧，从伦敦的城市，伦敦的金融区转移到欧洲大陆的工作和资产数量一直有限（根据EY对英国222家主要金融机构的一项调查，自公投以来，英国222个主要金融机构的工作数量已转移到该大陆，自公投左右左右约为7,600）。说，谈判很困难：虽然英国希望保持其作为欧洲金融中心的地位，并通过放松管制来增强其国际竞争力，但欧盟希望打破其对城市的依赖。根据谈判的方向，可以将更多的就业机会和资产转移到欧洲大陆。
ITU-T G 系列建议书 – 补编 41
遵守本出版物是自愿的。但是，出版物可能包含某些强制性规定（例如，为了确保互操作性或适用性），并且当满足所有这些强制性规定时，即符合本出版物。使用“应当”或其他强制性语言（例如“必须”）及其否定等价词来表达要求。使用这些词语并不表示要求任何一方遵守本出版物。
![arXiv:2309.05253v1 [quant-ph] 2023 年 9 月 11 日](/simg/a\a918c2678eeb47b4e561d6dda5a0cf6c67c0d39f.webp)
arXiv:2309.05253v1 [quant-ph] 2023 年 9 月 11 日
我们探索量子信息中对称性和随机性之间的相互作用。采用几何方法，如果状态与以群 H 为特征的对称变换相关，则我们认为状态是 H 等价的。然后，我们在均匀空间 U /H 上引入哈尔测度，以表征 H 等价系统的真正随机性。虽然数学家对这种数学机制进行了深入研究，但它在量子信息中的应用有限：我们相信我们的工作是利用均匀空间来表征量子信息中对称性的第一个例子。接下来讨论了真正随机性的近似，从 t 独立近似开始，并定义 U /H 和 H 等价状态的 t 设计。进一步过渡，我们探索伪随机性，在均匀空间内定义伪随机幺正和状态。最后，作为我们研究成果的实际证明，我们研究了均匀空间中量子机器学习假设的可表达性。我们的工作为量子世界中随机性和对称性的关系提供了新的视角。
HDR研究计划 摇头丸/MDMA使用和市场在澳大利亚，2013 - 2022年 2024研究监督荣誉和法医硕士 城市规划学士学位（荣誉）3362 PSYC3341发展心理学-2023
您的答案需要提供任何先前的学位及其所拥有的研究经验的详细信息。对于具有荣誉学士学位的申请人或通过研究硕士学位的申请人，通常是所有需要的。对于其他学位，您必须提供研究经验和最新研究成果的证据，以确立与这些资格的等价性。有关更多详细信息，请参见网站。
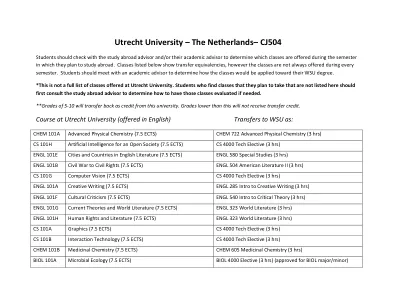
UTRECHT大学 - 荷兰 - CJ504 纤维金属的损伤耐受性和耐用性...
学生应与留学顾问和/或其学术顾问联系，以确定他们计划出国留学的学期提供了哪些课程。下面列出的类显示了转移等价，但是课程并不总是在每个学期期间提供。学生应与学术顾问会面，以确定如何将课程应用于其WSU学位。
分布自由条件独立性检验及其在因果发现中的应用
本文关注的是条件独立性的检验。我们首先建立条件独立性和相互独立性之间的等价性。基于这种等价性，我们提出了一个指标，通过量化变换变量之间的相互依赖性来衡量条件依赖性。所提出的指标有几个吸引人的特性。（a）它是无分布的，因为所提出的指标的限制零分布不依赖于数据的总体分布。因此，可以通过模拟列出临界值。（b）所提出的指标范围从零到一，当且仅当条件独立性成立时才等于零。因此，它在备选假设下具有非平凡的力量。（c）它对异常值和重尾数据具有鲁棒性，因为它对条件严格单调变换不变。（d）它的计算成本低，因为它包含一个简单的闭式表达式，可以在二次时间内实现。（e）它对涉及计算所提出的指标的调整参数不敏感。 (f) 新指数适用于多变量随机向量以及离散数据。所有这些属性使我们能够将新指数用作各种数据的统计推断工具。通过广泛的模拟和因果发现的实际应用证明了该方法的有效性。
自由能原理的物理原理有多特殊？
自由能原理 (FEP) 指出任何动力系统都可以解释为对其周围环境进行贝叶斯推理。在这项工作中，我们深入研究了在最简单的系统集——弱耦合非平衡线性随机系统中推导 FEP 所需的假设。具体来说，我们探索 (i) 对系统统计结构的要求有多普遍，以及 (ii) FEP 对此类系统行为的信息量有多大。我们发现 FEP 的两个要求——马尔可夫毯子条件（即排除内部和外部状态之间直接耦合的统计边界）和对其螺线管流的严格限制（即驱动系统失衡的趋势）——仅对非常狭窄的参数空间有效。合适的系统需要不存在感知-动作不对称，这对于与环境相互作用的生命系统来说极不寻常。更重要的是，我们观察到，论证中数学上的核心步骤，即把系统的行为与变分推理联系起来，依赖于系统平均状态的动态与这些状态的平均动态之间的隐式等价性。这种等价性即使对于线性系统也不成立，因为它需要有效地与系统的相互作用历史脱钩。这些目标
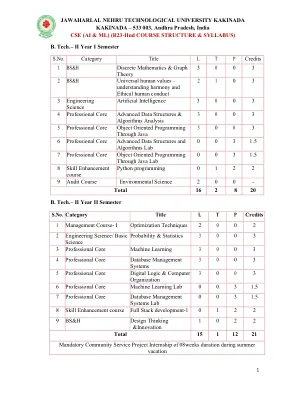
533 003，安得拉邦，印度 CSE（AI 和 ML）（R23-...
(L1) 第一单元：数理逻辑：命题演算：语句和符号、联结词、合式公式、真值表、同义反复、公式等价性、对偶律、同义反复蕴涵、范式、语句演算的推理理论、前提的一致性、间接证明方法、谓词演算：谓词、谓词逻辑、语句函数、变量和量词、自由和有界变量、谓词演算的推理理论。第二单元：集合论：集合：集合上的运算、包含-排斥原理、关系：性质、运算、分割和覆盖、传递闭包、等价性、兼容性和偏序、哈斯图、函数：双射、组合、逆、排列和递归函数、格及其性质。第三单元：组合学和递归关系：计数基础、排列、重复排列、循环和限制排列、组合、限制组合、二项式和多项式系数和定理。递归关系：生成函数、序列函数、部分分式、计算生成函数系数、递归关系、递归关系公式、通过代换和生成函数解决递归关系、特征根法、解决非齐次递归关系
不等式问题 1 的解答 - unipr
已知二次不等式的解等价于抛物线 1 的正点或负点的轨迹，我们推断不等式 x 2 − 1 > 0 在区间 ( −∞ , x eq 1 1 ) ∪ ( x eq 1 2 , ∞ ) = ( −∞ , − 1) ∪ (1 , ∞ ) 内有解（如果不等式的符号为 " ≥ "，则区间为 ( −∞ , − 1] ∪ [1 , ∞ ) ，即包含根）。第二个不等式属于 ax 2 + bx + c ≤ 0 类型，其中 a > 0 ，因此解集由区间 [ x eq 2 1 , x eq 2 2 ] = [ − 2 , 2] 给出。类似推理，可知第三个不等式的解集由 ( −∞ , 2] ∪ [3 , ∞ ) 给出。