XiaoMi-AI文件搜索系统
World File Search System对粒子系统和神经网络应用的一般可控性
摘要。存在许多具有对称性的系统的示例,并且可以通过具有对称性的控件进行监视。由于沿进化保留了对称性,因此不可能完全可控,并且必须将可控性视为具有相同对称性的状态的内部。我们证明,具有对称性的通用系统在这个意义上是可以控制的。该结果具有多种应用,例如:(i)当粒子之间相互作用的内核扮演均值场控制的作用时,粒子系统的一般可控性; (ii)在具有边界的歧管上对向量场的家庭的一般可控性; (iii)具有“通用”自发型层的神经网络体系结构的通用介绍 - 在最近的神经网络体系结构中,例如在变形金刚体系结构中的一种无处不在的层。我们开发的工具可以帮助解决模棱两可系统控制的其他各种问题。
三粒子阿哈罗诺夫-玻姆效应
“爱因斯坦-波多尔斯基-罗森 (EPR) 悖论的建立导致从量子信息的角度提供依赖于观察者的量子态描述。虽然这个问题基于单粒子系统,但可以扩展到多个相同粒子系统。我们提供了实验方案来阐明对相同粒子的量子态描述。该实验方案用于三粒子阿哈罗诺夫玻姆效应。”
概率论者的量子力学目录
现代概率的许多主题在数学物理和量子力学中都有对应内容。例如,抛物线 Anderson 模型的研究与 Anderson 局域化有关;相互作用粒子系统和自旋系统与量子自旋系统和量子多体理论有关;高斯自由场以及 Malliavin 微积分与欧几里得量子场论有关。这些笔记的目的是为具有概率背景的数学家介绍量子力学,提供基本的直觉和一本方便查阅数学物理文献的词典。重点是与概率的联系,特别是马尔可夫过程,而不是偏微分方程和谱理论。
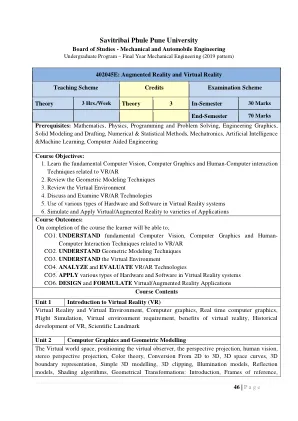
增强现实和虚拟现实 - MMIT
输入/输出设备:输入(跟踪器、传感器、数字手套、运动捕捉、基于视频的输入、3D 菜单和 3D 扫描仪等)、输出(视觉/听觉/触觉设备)通用 VR 系统:简介、虚拟环境、计算机环境、VR 技术、交互模型、VR 系统、虚拟环境动画:简介、数字动力学、线性和非线性插值、物体动画、线性和非线性平移、形状和物体之间、无变形、粒子系统物理模拟:简介、在重力场中下落的物体、旋转轮、弹性碰撞、抛射物、单摆、弹簧、飞机飞行动力学
物理学学士学位 (02133203)
SI 单位。有效数字。波:强度、叠加、干涉、驻波、共振、拍频、多普勒。几何光学:反射、折射、镜子、薄透镜、仪器。物理光学:杨氏干涉、相干性、衍射、偏振。流体静力学和动力学:密度、压力、阿基米德原理、连续性、伯努利。热:温度、比热、膨胀、热传递。矢量。点的运动学:相对运动、抛射运动和圆周运动。动力学:牛顿定律、摩擦力。功:点质量、气体(理想气体定律)、引力、弹簧、功率。动能:保守力、引力、弹簧。能量守恒。动量守恒。冲量和碰撞。粒子系统:质心、牛顿定律。旋转:扭矩、角动量守恒、平衡、重心。
狄拉克和非相对论量子振子的信息论分析
在过去的几十年里,人们对利用不同密度泛函研究量子力学系统的兴趣日益浓厚。信息论 [1] 提供的强大工具的使用受到了特别的关注,该工具旨在根据系统的代表性或特征概率分布对系统进行精确描述。这些工具的应用范围广泛,包括复杂程度各异的物理和化学对象,从少粒子系统 [2] 到结构复杂的分子 [3,4],再到多电子原子和离子 [5,6]。此外,对于给定系统,我们通常可以根据所追求的精度水平以及所考虑的变量来考虑不同的描述模型。在时间独立的量子力学框架中,对给定状态下的单粒子或多粒子系统的完整描述,需要了解相应的波函数 (r 1 , . . . , rn ),它是特征值方程的相应解
基于白蛋白纳米颗粒的药物输送系统
摘要:纳米粒子系统在药物输送方面被广泛研究。其中,白蛋白具有优异的生物相容性和增强的靶向能力,似乎是药物输送的有前途的载体。白蛋白纳米粒子在许多疾病治疗中备受青睐,因为它们具有适合修饰的化学基团、适合细胞粘附的细胞结合位点以及适合生成纳米复合物的蛋白质药物亲和力。本文总结了白蛋白纳米粒子的最新制造技术、修饰策略和应用。我们首先从优缺点两方面讨论各种白蛋白纳米粒子的制造方法。然后,我们对修饰部分进行了全面的介绍,包括有机白蛋白纳米粒子、金属白蛋白纳米粒子、无机白蛋白纳米粒子和基于白蛋白纳米粒子的混合物。最后,我们进一步介绍了用于各种重大疾病的白蛋白纳米粒子。
快速行驶车辆产生的灰尘行为的实时模拟
模拟物理上逼真的复杂尘埃行为在培训、教育、艺术、广告和娱乐中非常有用。目前还没有公开的模型可以实时模拟行驶车辆产生的尘埃行为。在本文中,我们使用粒子系统、计算流体力学和行为模拟技术来实时模拟尘埃行为。首先,我们分析影响尘埃产生的力和因素以及尘埃粒子产生后的行为。然后,我们构建基于物理的经验模型来生成尘埃粒子并相应地控制行为。我们通过将尘埃行为分为三个阶段并为每个阶段建立简化的粒子系统模型来进一步简化数值计算。我们采用运动模糊、粒子混合、纹理映射和其他计算机图形技术来实现最终结果。我们的贡献包括构建基于物理的经验模型来生成尘埃行为并实现对行为的实时模拟。
快速行驶车辆产生的灰尘行为的实时模拟
模拟物理上逼真的复杂粉尘行为在培训、教育、艺术、广告和娱乐方面非常有用。目前还没有公开的模型可以实时模拟行驶车辆产生的粉尘行为。在本文中,我们使用粒子系统、计算流体动力学和行为模拟技术来实时模拟粉尘行为。首先,我们分析影响粉尘产生的力和因素以及粉尘颗粒产生后的行为。然后,我们构建基于物理的经验模型来生成粉尘颗粒并相应地控制行为。我们通过将粉尘行为分为三个阶段,并为每个阶段建立简化的粒子系统模型,进一步简化数值计算。我们采用运动模糊、粒子混合、纹理映射和其他计算机图形技术来实现最终结果。我们的贡献包括构建基于物理的经验模型来生成尘埃行为并实现实时行为模拟。