XiaoMi-AI文件搜索系统
World File Search System基于电动力学的具有玻恩散射的量子门优化
本文提出利用电子散射来实现由三个量子比特控制的幺正量子门。利用费曼规则,我们找到了外部电磁源散射跃迁振幅的表达式。在此背景下,散射振幅被建模为一个状态可调节的幺正门。实现门所需的矢量势的最优值是通过最小化设计门和目标门之间的差异来获得的,以总消耗能量为约束。设计算法是通过将得到的积分方程离散化为矢量方程而得到的。该设计算法可应用于量子计算、通信和传感等各个领域。它为开发用于量子信息处理的高效和精确的门提供了一种有前途的方法。此外,这种方法还可以扩展到设计多量子比特系统的门,这对于大规模量子计算至关重要。该算法的使用可以大大促进实用量子技术的发展。
关于给定色数图中奇数圈的加强
我们遵循 [9, 13] 中的符号。设 G 为图。对于 V(G) 的非平凡划分 (A,B),1如果路径 P 的一端在 A 中而另一端在 B 中,则我们称路径 P 为 A - B 路径。设 P 为图 G 中的一条路径。设 | P | 为 P 中的边数。如果 | P | 为偶数(分别为奇数),则我们称 P 为偶数(分别为奇数)。设 C 为按循环顺序具有顶点 v 0 ,v 1 ,...,vt − 1 的环。设 C i,j 表示 C 的子路径 vivi +1...vj,其中索引取自加法群 Z t 。设 H 为 G 的子图。如果顶点 v ∈ V ( G ) − V ( H ) 在 G 中与 V ( H ) 中的某个顶点相邻,则我们称 H 和顶点 v ∈ V ( G ) − V ( H ) 在 G 中相邻。设 NG ( H ) = S v ∈ V ( H ) NG ( v ) − V ( H ) 且 NG [ H ] = NG ( H ) ∪ V ( H )。对于 S ⊆ V ( G ),如果 V ( G ′ ) = ( V ( G ) − S ) ∪{ s } 且 E ( G ′ ) = E ( G − S ) ∪{ vs : v ∈ V ( G ) − S 与 G 中的 S 相邻 } ,我们称图 G ′ 是通过将 S 收缩为顶点 s 而从 G 得到的。如果 G − v 包含至少两个分支,则连通图 G 的顶点 v 是 G 的割顶点。 G 中的块 B 是 G 的最大连通子图,使得不存在 B 的割顶点。注意块是孤立顶点、边或2连通图。G 中的端块是 G 中最多包含一个 G 的割顶点的块。如果 G 是图并且 x, y 是 G 的两个不同顶点,我们称 ( G, x, y ) 为有根图。有根图 ( G, x, y ) 的最小度为 min { d G ( v ) : v ∈ V ( G ) −{ x, y }} 。如果 G + xy 是2连通的,我们还称有根图 ( G, x, y ) 是2连通的。我们称 k 条路径或 k 条循环 P 1 , P 2 , . . . , P k 为
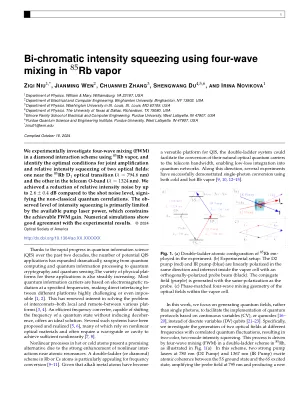
利用四波混频实现双色强度压缩
得益于过去 20 年量子信息科学 (QIS) 的快速发展,潜在的 QIS 应用数量急剧增加,包括量子计算和量子信息处理、量子密码和量子传感。这些应用的物理平台种类也在稳步增加。大多数量子信息载体基于特定频率的电磁辐射,因此不同平台之间的直接接口极具挑战性,甚至不可能实现 [1,2]。这重新引起了人们对解决不同平台之间本地和远程互连问题的兴趣 [3,4]。高效的频率转换器能够改变量子态的频率而不会引起退相干,因此提供了一种理想的解决方案。已经提出并实现了几个这样的系统 [5,6],其中许多依赖于非线性光学材料,并且通常需要波导或腔体来实现足够的非线性 [7,8]。热原子或冷原子中的非线性过程是一种很有前途的替代方案,因为原子共振附近的非线性相互作用得到了强烈的增强。Rb 或 Cs 原子中的双梯形(或菱形)方案对于频率转换特别有吸引力 [9-11]。鉴于碱金属原子已成为
通过超导Josephson连接
编辑器:J。Hisano通过引人入胜的𝑈(1)𝐵-𝐿标准模型的扩展,可以很好地激发携带𝐵-𝐿电荷之间的颗粒之间的新第五力。量规玻色介质Féeton也是暗物质候选人。在这封信中,我们提出了一种新型的实验设计,以检测使用超导约瑟夫森连接的第五力引起的量子相差异。我们发现,当仪表玻色子质量范围内时,实验对量规耦合具有最佳的敏感性。01 eV至10 eV,这是Féeton暗物质的一个有趣的质量区域。这为毫米以下小规模的新物理学测量开辟了新的途径。
通过实验测试量子场论概念......
指定多体量子系统状态所需的参数数量随其成分数量呈指数增长。这一事实使得在计算上难以准确描述动力学并在微观层面上表征状态。在本论文中,我们采用量子场论概念来实验性地表征远离平衡态的旋量玻色气体。首先,我们引入相关概念,这些概念为新兴宏观现象提供有效描述,其公式与超冷原子系统的能力相匹配。在我们的实验研究中,我们在准一维陷阱几何中采用 87 Rb 旋量玻色-爱因斯坦凝聚态。我们通过测量自旋自由度的波动来探索相图作为有效二次塞曼位移的函数,并确定三个不同的相。利用这些知识,我们研究了在分离不同相的量子相变中发生瞬时淬灭后发生的不稳定性。这些不稳定性使我们能够以高度可控的方式将系统驱动到远离平衡状态。在淬火后的很长一段时间内,我们观察到与非热不动点的出现相关的通用动力学。横向自旋角取向的结构因子具有在时间和空间中的重新缩放,具有通用指数以及通用缩放函数。利用实验控制,我们探测了这种现象对初始条件细节的不敏感性。复值横向自旋场的空间分辨快照允许提取单粒子不可约关联函数,这是量子有效作用的基石。我们发现在高度占据状态下出现了低动量的 4 顶点的强烈抑制。引入的概念与提出的实验适用性为研究多体系统在其演化的所有阶段提供了新方法:从初始不稳定性和远离平衡的瞬态现象到最终的热化。
自旋系综中的数相不确定关系和二分纠缠检测
我们提出了一种基于分裂自旋系综中类数相不确定关系来检测二分纠缠的方法。首先,我们推导出一个不确定关系,该关系在自旋系统中起到数相不确定性的作用。重要的是,该关系具有明确定义且易于测量的量,并且不需要假设无限维系统。基于这种不确定关系,我们展示了如何检测许多自旋 1/2 粒子的非极化 Dicke 态中的二分纠缠。将粒子分成两个子系综,然后在这两个部分上进行局部集体角动量测量。首先,我们提出一个二分爱因斯坦-波多尔斯基-罗森 (EPR) 转向标准。然后,我们提出一种可以在这种系统中检测二分纠缠的纠缠条件。通过将这些标准应用于 K. Lange 等人给出的最新实验,我们证明了这些标准的实用性。 [Science 360, 416 (2018)] 在冷原子的玻色-爱因斯坦凝聚态中实现狄克态,其中两个子集合在空间上彼此分离。如果考虑分裂自旋压缩态,我们的方法也同样有效。我们全面展示了如何处理实验缺陷,例如包括分区噪声在内的非零粒子数方差,以及尽管理想情况下 BEC 占据单一空间模式,但实际上其他空间模式的数量无法完全抑制这一事实。
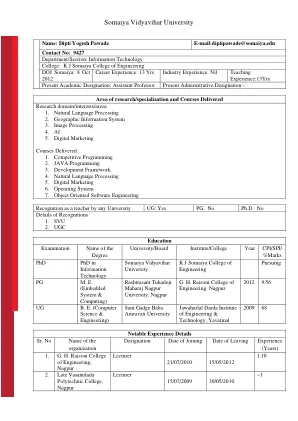
索迈亚维迪亚维哈尔大学
和自动化(ICCUBEA),Pimpri Chinchwad 工程学院(PCCOE),浦那,2017 年 8 月 17-18 日,IEEE 数字图书馆论文集。52. 34. Dipti Pawade、Harshada Sonkamble、Yogesh Pawade,“具有高级功能的基于 Web 的医院管理系统”,工程、科学和技术现代趋势国际会议 (ICMTEST-16),2016 年 4 月 9 日和 10 日,计算和通信最新和创新趋势国际期刊 (IJRITCC) 论文集。53. Dipti Pawade、Khushaboo Rathi、Shruti Sethia、Kushal Dedhia,“产品评论分析