XiaoMi-AI文件搜索系统
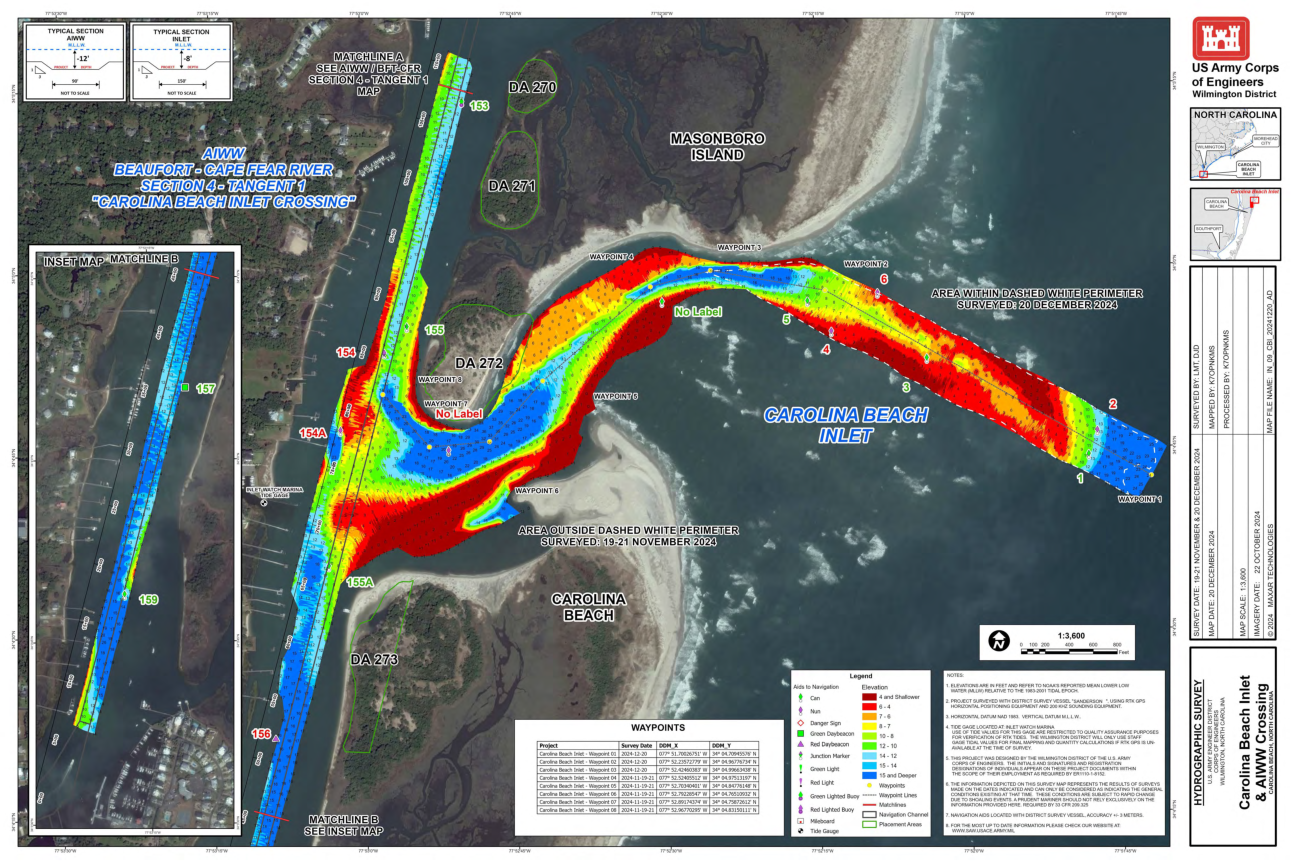
World File Search System卡罗莱纳海滩入口 - 美国陆军工程兵团
5. 此项目由美国陆军工程兵团威尔明顿区设计。个人姓名首字母和签名以及注册 C) 职务名称出现在这些项目文件中,属于 ER1110-1-8152 所要求的 IR 工作范围内。0 a::: 6. 此测量地图上描述的信息代表在所示日期进行的测量结果,只能被视为表明当时存在的一般 C 条件 E。这些条件可能会因浅水事件而迅速变化。谨慎的海员不应完全依赖 > :::c 此处提供的信息。33 CFR 209.325 要求
卡罗来纳大学三世分校创新研发
学院在研究、教学和技术转让方面的目标是: • 开展大数据分析的跨学科基础研究,汇集统计学、应用数学、计算机科学和机器学习方面的专业知识,促进不同领域的合作。 • 开展面向金融应用的应用跨学科研究。这些研究可能会产生“衍生品”或“初创”公司。 • 通过大数据硕士课程和数据分析和数据管理不同领域的几门短期课程提供大数据分析教育。此外,学院还将根据要求为组织提供内部培训。 • 与私人和公共合作伙伴合作,为他们在处理、存储和分析大数据集方面的问题提供解决方案。
卡罗来纳州锂:拟议的集成项目
Using a Modified Humidity Cell) • Phase I Cultural Resource Survey • Leachate Environmental Assessment Framework (LEAF) Testing • Noise Study • Road Abandonment Survey • Stream Flow Study • Technical Report Summary Carolina Lithium Project • Toxicity Testing of Lithium Hydroxide Conversion Tailings • Traffic Impact Analysis Scoping Report • U.S. Army Corps of Engineers Statement of Findings Environmental
超越体素预测的不确定性:识别值得信赖的脑损伤
摘要。深度神经网络已成为自动分割 3D 医学图像的黄金标准方法。然而,由于缺乏对提供的结果进行可理解的不确定性评估,临床医生仍然无法完全接受它们。大多数量化不确定性的方法,例如流行的蒙特卡罗 dropout,都限制了体素级预测的某种不确定性。除了与真正的医学不确定性没有明确的联系外,这在临床上也不令人满意,因为大多数感兴趣的对象(例如脑病变)都是由体素组组成的,而体素组的整体相关性可能不会简单地归结为它们各自不确定性的总和或平均值。在这项工作中,我们建议使用创新的图形神经网络方法超越体素评估,该方法由蒙特卡罗 dropout 模型的输出训练而成。该网络允许融合三个体素不确定性估计量:熵、方差和模型置信度;并且可以应用于任何病变,无论其形状或大小如何。我们证明了我们的方法在多发性硬化症病变分割任务中的不确定性估计的优越性。
迪亚巴特方法测定同质异形体自由能 - UCL Discovery
晶格切换蒙特卡罗和相关的 diabat 方法已成为计算同质异形体之间自由能差异的有效而准确的方法。在这项工作中,我们引入了从一种分子晶体中的参考位置和位移到另一种分子晶体中的位置和位移的一对一映射。映射的两个特点有助于使用晶格切换蒙特卡罗和相关的 diabat 方法计算同质异形体自由能差异。首先,映射是单一的,因此其雅可比矩阵不会使自由能计算复杂化。其次,对于任意复杂度的分子晶体,映射都很容易实现。我们通过计算苯和卡马西平同质异形体之间的自由能差异来证明映射。热力学循环的自由能计算,每个循环都涉及三个独立计算的同质异形体自由能差异,都以高精度返回到起始自由能。因此,这些计算提供了方法的力场独立验证,并使我们能够估计单个自由能差异的精度。
弗里蒙特公用事业部
公用事业部弗里蒙特市向弗里蒙特市,内布拉斯加州及周边地区提供天然气,电气,水和废水服务。弗里蒙特(Fremont)是一个位于内布拉斯加州东部的成长社区,人口约有27,000人。弗里蒙特公用事业部(FUD)拥有并运营三个煤炭/天然气发射的蒸汽轮机,一辆双燃料燃烧涡轮机和两个社区太阳能电池阵列。FDU还拥有40.89兆瓦的风力资源的购买电力协议(PPA),并与西部地区电力局(WAPA)达成了5 MW的容量协议。FUD是西南电力池的参与者,与奥马哈公共电力区(OPPD)有三个系统互连和互连协议。弗里蒙特(Fremont)有20兆瓦的牢固传输,从杨木风能到弗里蒙特(Fremont),从OPPD到弗里蒙特(Fremont)的5兆瓦企业传输以及从WAPA到弗里蒙特(Fremont)的5兆瓦传输。1.1.1 WAPA IRP要求1.1.1 WAPA IRP要求
产品数据表:罗斯蒙特 700XA
TCD 是大多数应用的首选检测器,因为它对天然气、轻质炼油厂和碳氢化合物加工气体分析中感兴趣的成分具有通用响应。Rosemount 700XA GC 中的 TCD 能够执行许多低百万分率测量要求的应用,从而测量远远超出其他设计中正常范围的量程。当可以使用简单而坚固的 TCD 时,这大大简化了 GC 设计并降低了最终用户的成本。
多项式混乱扩展和机器学习
PCE的主要特征是正交多项式家族与输入特征的统计数据之间有很强的联系。这种连接的好处是双重的。首先,如果选择正交多项式与输入数据的概率分布一致,则可以提高PCE响应表面的质量。其次,基于PCE的响应表面的利用简化了灵敏度分析和不确定性定量,因为可以在没有蒙特卡罗模拟的情况下分析地计算多种灵敏度指标。
税率套利实现长期收益以实现……
1 Constantinides 1983 使用期权理论框架量化税收管理投资中时机损失和收益实现的价值。Wilcox、Horvitz 和 diBartolomeo 2006 对税收管理投资进行了更近期、更全面的阐述。Geddes、Goldberg 和 Bianchi (2015) 说明了指数化损失收获投资组合作为定期产生资本收益的资产配置的一部分的价值。2 Jeffrey 和 Arnott 1993;Arnott、Berkin 和 Ye 2000;以及 Arnott、Berkin 和 Bouchey 2011 证明了税收管理对应税投资者股票投资组合的重要性。Berkin 和 Ye 2003 使用蒙特卡罗模拟量化最高进先出 (HIFO) 会计的收益,以及在股票特定风险相对较高、平均回报率较低和股息收益率较高的市场中损失收获的增量收益。 Berkin 和 Luck 2010 使用蒙特卡罗模拟来展示税收管理在扩展股票策略中的好处。Bergstresser 和 Pontiff 2013 使用实证数据记录了税收对投资组合价值、增长和规模的影响,并表明税收加剧了股票溢价之谜。Israel 和 Moskowitz 2012 探讨了税收管理对规模、价值、增长和动量的影响。Geddes 2011 和 Geddes 和 Tymoczko 2019 使用蒙特卡罗模拟来展示单独管理账户中的损失收割相对于持有交易所交易基金 (ETF) 的税后收益。Sialm 和 Sosner 2018 量化了税收管理的 130-30 和多空市场中性策略的税后回报。 Santodomingo、Nemtchinov 和 Li (2016) 和 Goldberg、Hand 和 Cai (2019a) 使用历史回溯测试研究了流行因子倾向的税后回报和风险状况。Goldberg、Hand 和 Cai (2019b) 描述了指数跟踪和无碳策略的类似概况。3 Constantinides (1984);Dammon、Dunn 和 Spatt (1989);以及 Stein、Vadlamudi 和 Bouchey (2008) 使用蒙特卡洛模拟来评估税率套利策略。