XiaoMi-AI文件搜索系统
World File Search System量子引力导论 I+II
2 约束哈密顿系统 13 2.1 没有规范对称性的哈密顿系统 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ................................................................................................................................................................................................................. 16 2.2.2 稳定性算法....................................................................................................................................................................................................... 17 2.2.3 规范变换....................................................................................................................................................................................................... 19 2.2.4 场论....................................................................................................................................................................................................... 19 2.2.4 场论....................................................................................................................................................................................................... 19 . ... 24 2.3.3 小偏移:量化 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ...
kazi Nazrul大学 - 物理系
系统。回顾拉格朗日形式主义; Lagarange方程的一些特定应用;小振荡,正常模式和频率。(5L)汉密尔顿的原则;变异的计算;汉密尔顿的原则;汉密尔顿原则的拉格朗日方程式; Legendre Transformation和Hamilton的规范方程;从各种原理中的规范方程式;行动最少的原则。(6L)规范变换;生成功能;规范转换的例子;集体财产; Poincare的整体变体;拉格朗日和泊松支架;无穷小规范变换;泊松支架形式主义中的保护定理;雅各比的身份;角动量泊松支架关系。(6L)汉密尔顿 - 雅各比理论;汉密尔顿汉密尔顿原理功能的汉密尔顿雅各比方程;谐波振荡器问题;汉密尔顿的特征功能;动作角度变量。(4L)刚体;独立坐标;正交转换和旋转(有限和无穷小);欧拉的定理,欧拉角;惯性张量和主轴系统;欧拉方程;重型对称上衣,带有进动和蔬菜。(7L)非线性动力学和混乱;非线性微分方程;相轨迹(单数点和线性系统);阻尼的谐波振荡器和过度阻尼运动; Poincare定理;各种形式的分叉;吸引子;混乱的轨迹; Lyaponov指数;逻辑方程。(6L)相对论的特殊理论;洛伦兹的转变; 4个向量,张量,转换特性,度量张量,升高和降低指数,收缩,对称和反对称张量; 4维速度和加速度; 4-Momentum和4 Force;
许多粒子系统的量子理论
Alexander L. Fetter,John Dirk Walecka和Leo P. Kadanoff的多粒子系统的量子理论是一本全面的教科书,提供了对非同性主义多个粒子系统的独立介绍。本书提供了对形式主义和应用的统一处理,使其成为该领域的研究生和老师的宝贵资源。它涵盖了诸如第二量量化,统计力学,规范变换以及对物理系统的应用,包括核物质,声子,电子,超导性和超流体氦气。文本旨在促进从上量子力学课程到解释有关多体问题的大量文献的实际过渡。
M.Sc. (植物学)
在4维Minkowski空间,Lorentz标量,4个矢量和4个量的正交转换中,Minkowski空间中的4次量,协变形式的力学法律以及适当的时间间隔,4个矢量位置,4个矢量的位置,4个载体速度和4个载体的速度和4个载体的力量,纽顿的力量的形式相互关系,相互关系,相互关系。结果:学生将能够记住并得出四个矢量符号中的哈密顿力学,小振荡,规范变换,僵化的身体动力学和相对论力学的各种公式。他们将能够分析各种概念并解决与所获得的知识有关的问题。将所学的机械配方应用于不同主题的实践物理/科学问题,并了解其局限性及其对量子力学的影响。教科书:
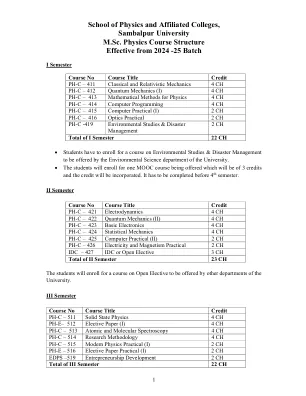
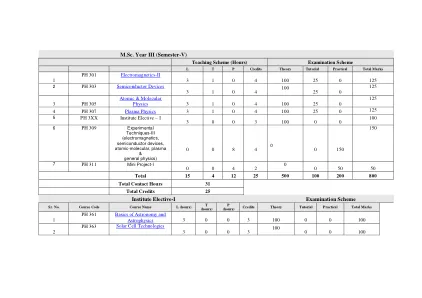
理学硕士第三年(第五学期)
教学大纲 电动力学 (08 小时) 电动势和运动电动势、法拉第电磁感应定律和磁场中的能量、麦克斯韦方程组、麦克斯韦如何固定安培定律、物质中的麦克斯韦方程组、边界条件 电动力学中的守恒定律 (06 小时) 连续性方程、坡印廷定理、电动力学中的牛顿第三定律、麦克斯韦应力张量、动量守恒定律、角动量 电磁波 (08 小时) 一维波、真空和物质中的电磁波、物质中的吸收和弥散、导波 势与场 (07 小时) 标量势和矢量势、规范变换、库仑规范和洛伦兹规范、延迟势、 Jefimenko 方程、Lienard-Wiechert 势、移动点电荷的场辐射(06 小时)电偶极子辐射和磁偶极子辐射、任意源的辐射、点电荷辐射的功率、辐射反应电动力学和相对论(07 小时)狭义相对论和相对论力学、相对论电动力学、场张量、张量符号中的电动力学。
量子参考框架之间动态转换的组结构
最近,显示出参考帧与量子系统相关联时,需要修改此类量子参考框架之间的转换定律以考虑参考帧的量子和动态特征。这导致了量子系统的相位空间变量的关系描述,量子系统的一部分是量子系统的一部分。虽然这种转换被证明是系统的哈密顿量的对称性,但对于它们是否享受群体结构,与Quantum机械师中的classical参考框架相似的问题仍然没有答案。在这项工作中,我们确定了包含量子参考框架的量子系统相空间上的规范变换,并表明这些转换封闭了由lie代数定义的组结构,这与量子机械的通常的galilei代数不同。我们进一步发现,这个新代数的要素实际上是先前确定的量子参考帧转换的构建块,我们是我们恢复的。最后,我们展示了如何通过采用控制惯性转换的量子性质引入的附加非交通性的参数的零极限来从量子参考框架之间的一组转换中获得的经典参考框架之间的转换。
冲浪变形器减轻表面动态缺陷代码 - ...
摘要 — 在本文中,我们介绍了 Surf-Deformer,这是一种代码变形框架,可将自适应缺陷缓解功能无缝集成到当前的表面代码工作流程中。它根据基本规范变换设计了几种基本变形指令,这些指令可以组合起来探索比以前的方法更大的设计空间。这使得针对特定缺陷情况定制的变形过程更加优化,以最少的量子位资源更有效地恢复变形代码的 QEC 能力。此外,我们设计了一种自适应代码布局,可以适应我们的缺陷缓解策略,同时确保逻辑操作的高效执行。我们的评估表明,Surf-Deformer 的表现优于以前的方法,可将各种量子程序的端到端故障率显著降低 35 倍至 70 倍,而与以前的方法相比,仅需要约 50% 的量子位资源即可实现相同的故障率。烧蚀研究表明,Surf-Deformer 在保留 QEC 能力方面超越了以前的缺陷去除方法,并通过实现近乎最佳的吞吐量来促进表面代码通信。索引词——量子误差校正、动态缺陷
YANG-MILLS理论中的全球仪表对称性和空间渐近边界条件
在阳米尔斯仪表上的欧几里得凯奇表面表面表面含有直接经验意义的仪表对称性组通常被认为是g des = g des = g i /g∞0,其中g i是一个具有边界的符号对称性和g∞0是其由构成理论构成的构成的构成的转化。这些群体分别被识别为渐近变化的仪表变换,以及渐近身份的量规变换。在Abelian案例中G = U(1)然后将其标识为全球仪表对称组,即u(1)本身。然而,在数学上还是概念上,这一说法的已知派生都是不精确的。我们针对阿贝里安和非亚伯仪理论严格得出了物理量规组。我们的主要新观点是,限制g i的要求不仅源于能量的有限,而要依赖于Yang-Mills理论的Lagrangian的要求,以在切实的捆绑包上定义以配置空间。此外,我们解释了为什么商恰好由每个同型类别的全球仪表组的副本组成,即使各种规范变换显然具有不同的渐近速率收敛速率。最后,我们在框架中考虑了Yang-Mills-Higgs理论,并表明渐近边界条件在不间断和破碎的相处有所不同。1
经典极限中的相干控制:光学晶格中的对称性破缺
分子过程的相干控制源于通向同一最终状态的多种途径 1、2 之间的干涉,通常是通过激光照射引起的。最近的理论研究表明,类似的过程可以出现在经典力学的某些场景中 3、4,并且这种控制可以在经典极限下持续存在 5。基于非线性响应和通过海森堡表示观察干涉的考虑 6、7 表明,当控制在经典极限下存活时,它之所以如此,是因为对量子动力学有贡献的干涉项是由外部驱动的,即与外部激光场的振幅成比例。从这个意义上说,量子干涉贡献在质上与双缝实验等中的贡献不同。负责量子控制的量子干涉现象存在非零经典极限的可能性很大,需要仔细探索。在本文中,我们通过计算研究了在预计可通过实验实现的拟议光晶格场景中接近经典控制极限的方法。该设计允许人们探索控制作为有效的 → 0 以及退相干对量子控制的比较影响。下面的计算结果还强调了经典规则动力学与混沌动力学领域的量子响应差异。作为一种特殊的控制场景,我们关注对称性破坏,其中空间对称系统被具有频率分量和 2 的激光场照射。这样的场产生相位可控的净偶极子或电流,而不会在电位中引入偏置(例如,参见参考文献 1、3、5、8-10)。我们提出的系统是一个移动或振动的一维光学晶格 11,12,如下图所示,通过规范变换,可以将其视为与空间均匀电场相互作用的静止空间对称周期势。我们考虑了 → 0 极限以及退相干的影响,后者
物理学硕士
Sarah Caudill,博士,路易斯安那州立大学,助理教授。专业领域:黑洞和中子星的引力波搜索、科学计算、机器学习。 Robert Fisher,(研究生项目主任),博士,加州大学伯克利分校,教授。专业领域:湍流基础物理学、科学计算、恒星形成和超新星。 Jong-Ping Hsu 博士 1969 罗彻斯特大学,校长教授。专业领域:时空对称性、量子杨-米尔斯引力、具有非积分相位因子的广义规范变换和夸克禁闭的可重整化模型 David Kagan,博士,剑桥大学,物理学专职讲师。专业领域:弦理论、量子引力、量子理论。 Christian McHugh,博士,北卡罗来纳大学教堂山分校,物理学专职讲师。专业领域:医学物理学、磁共振成像、化学交换核磁共振波谱、超极化氙。 Grant O'Rielly,博士,墨尔本大学,副教授。专业领域:中等能量光核物理、少体系统、介子光生成、基本核对称性。 Renuka Rajapakse,博士,康涅狄格大学,物理学专职讲师。专业领域:量子光学、计算物理、量子计算和原子物理。 Jay (Jianyi) Wang,(主席),博士,田纳西大学诺克斯维尔分校,教授。专业领域:电子、原子和光学过程的理论与模拟、离子-固体和离子-表面相互作用、计算物理。