XiaoMi-AI文件搜索系统
World File Search System离子束源的过去、现在和未来
对各种太空推进方法的分析研究表明,电加速材料可实现极高的排气粒子速度。这意味着推进剂材料将被非常有效地用于产生推力,而推力从定义上讲就是高比冲。化学火箭的比冲受化学反应限制,在 100 以下。(单位是秒,作为近似值,可以视为 1 磅推进剂产生 1 磅推力的时间长度。)另一方面,通过计算,电气系统应该能够达到 1,000 到 10,000 秒之间的值。比冲的最佳值是根据特定任务的计算确定的,并与在给定时间内完成任务所需的能量有关。
有理近似,多维持续分数和晶格还原
持续分数类型的扩展目的(除其他属性)提供了越来越好的实际数字合理性二磷酸近似值。更重要的是,预期的多维持续分数将产生越来越更好的理性近似值,具有相同的分母B旧p上p左括号n右括号n右括号基线除以q上额本额外额外的额外额外额外的额外括号n右括号n右括号n右额外的左额外额外的固定额外的固定额外的固定额外的基线置于左额外的基线,并置于固定的左额外的固定范围内置额的固定范围内的右置态固定范围内的右手置态置于固定范围内的右手置态,并置于左右的左态,并置于左右的固定。 COMMA ELLIPSIS P下标D上标左括号n右括号基线除以Q上标左括号n右括号n右括号右括号右括号n下标n double double doupter n p(n) /q(n) /q(n)=(p(n)1 /q(n)1 /q(n)1 /q(n),。< /div> < /div> < /div> < /div> < /div>。。p(n)d /q(n))n∈Nd -tuples粗体斜体alpha等于左括号alpha 1 comma ouripsis chripsis comma comma comma comma alpha alpha下标d基线右括号α=(α1,。< /div>,。< /div>。。,αd)实数,分数p下标i上标左括号n右括号基线除以q superscript左括号n右括号n右括号p(n)i /q(n)i /q(n),收敛到lpha sisscriptiαiαiiαiiαiiαiiαi小于或等于i小于或等于或等于或等于或等于或等于或等于d或equals d by或equals d by或equal d f d f d by或equals d by或equals d use。已知通常的常规持续分数为正实数提供了极好的(甚至是最好的)合理近似值[41,89]。
安全数据表:2-吡咯烷酮
佩戴合适的手套。根据 EN 374 测试的化学防护手套是合适的。对于特殊用途,建议与这些手套的供应商一起检查上述防护手套的耐化学性。这些时间是 22°C 和持续接触时测量的近似值。由于加热物质、体热等导致的温度升高以及拉伸导致的有效层厚度减小会导致突破时间显著缩短。如有疑问,请联系制造商。在约 1.5 倍大/小的层厚度下,相应的突破时间加倍/减半。数据仅适用于纯物质。当转移到物质混合物时,它们只能被视为指导。
安全数据表:DABCO®
佩戴合适的手套。根据 EN 374 测试的化学防护手套是合适的。对于特殊用途,建议与这些手套的供应商一起检查上述防护手套的耐化学性。这些时间是 22°C 和持续接触时测量的近似值。由于加热物质、体热等导致的温度升高以及拉伸导致的有效层厚度减小会导致突破时间显著缩短。如有疑问,请联系制造商。在约 1.5 倍大/小的层厚度下,相应的突破时间加倍/减半。数据仅适用于纯物质。当转移到物质混合物时,它们只能被视为指导。
通过优化德克萨斯州电网蓄电池的放置来减少排放
2 在尝试(但失败了)在我们自己的笔记本电脑上以合理的容量运行基础模型后,我们考虑过利用大学的远程计算资源,但经过深思熟虑后,我们一致认为使用更简单的模型可能会更有优势。我们相信,简化的模型将以更易理解和更直观的规模提供类似的见解,同时还能让我们完全透明地控制我们的优化算法。3 重要提示:这个模型就是所谓的合成电网测试用例。这意味着,虽然它基于来自现实世界的德克萨斯电网的数据,但它的规模要小得多。它的目的是通过提供德克萨斯州发电和配电能力的合理近似值,促进与我们项目类似的分析。
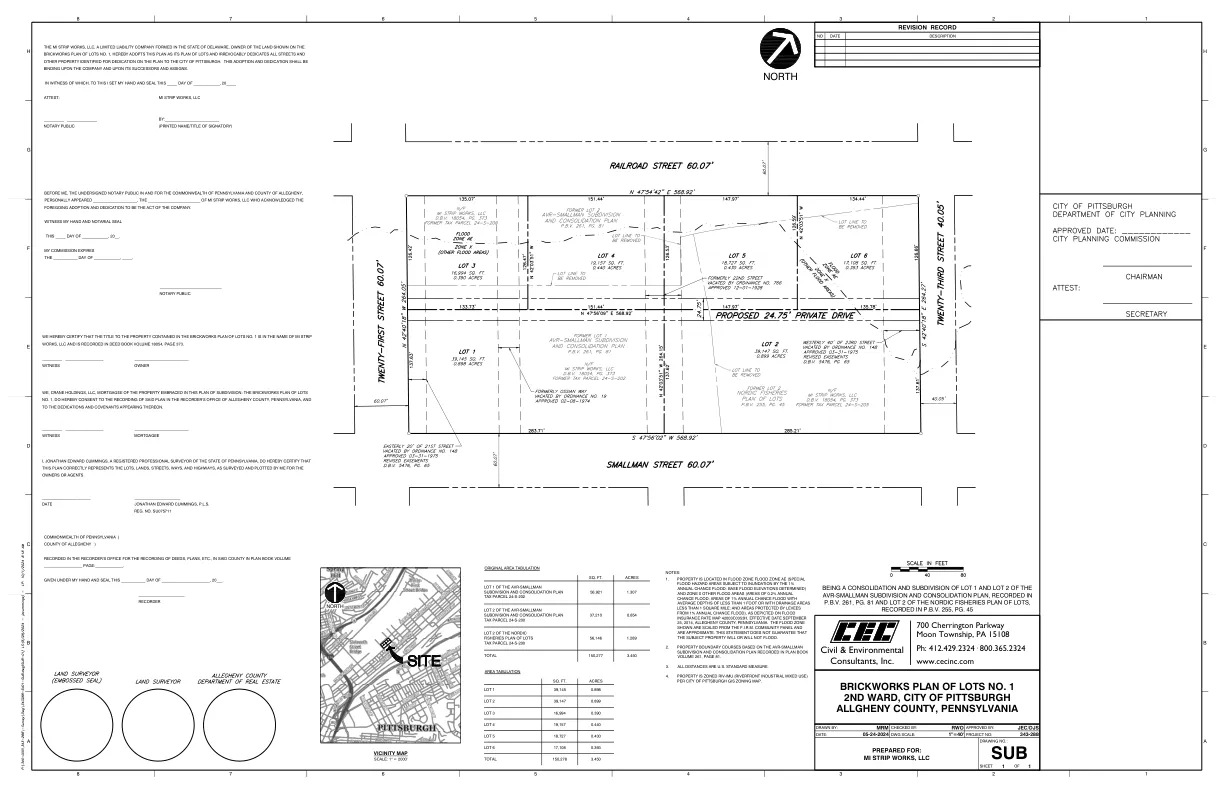
第二区 1 号地块北砖厂规划图,...
年度偶然洪水:确定的基准洪水高程)和区域 X 其他洪水区域(0.2% 年度偶然洪水区域;1% 年度偶然洪水区域,平均深度小于 1 英尺或排水面积小于 1 平方英里;以及受堤坝保护免受 1% 年度偶然洪水侵袭的区域),如洪水保险费率图 42003C0353H 所示,生效日期为 2014 年 9 月 25 日,宾夕法尼亚州阿勒格尼县。所示的洪水区域按公司社区面板的比例绘制,并且是近似值。本声明并不保证标的财产是否会被洪水淹没。
太空电子的质量特性实验室...
尽管有出色的计算机模型,但可以确保系统的质量特性(质量,重心(CG)位置,惯性矩(MOI),惯性(POI)的产物(POI)的唯一方法是正确的,就是在系统开发的各个阶段进行测量。惯性张量的模型,无论多么复杂,仍然只是理论上的近似值。计算机模型很少包括航空航天系统中包含的环氧,管道或布线。该模型不认识到泡沫和复合材料的密度在复杂的,有时是不可预测的方式方面变化。它通常无法解释皮肤厚度的变化。这些遗漏和变化可以轻松地占系统惯性矩的30%,并可能导致无法校正的CG偏移。
时间序列建模的条件流匹配
可以通过使用神经网络近似其矢量场来学习系统的不变动态,这是一种称为神经odes的概念(Chen等人。,2018b; Rubanova等。,2019年; Yildiz等。,2019年)。然而,这些模型的损失景观的复杂性随观察到的轨迹的长度而增加,因此它们的训练也无法收敛于中等长的观察范围(Ribeiro等人。,2020年; Metz等。,2022)。早期溶液将长轨迹分为较小的细分市场,并通过约束确保概率模型的连续性(Hedge等人。,2022; Iakovlev等。,2023)。然而,在没有离散近似值的情况下安装长轨迹仍然是一个空旷的问题。
随机量子电路采样:行人指南
为什么这一点很重要?为了证明量子霸权,我们最终要证明 Pr(S) 和 Pr(Scl) 之间存在可测量的差异。这是基于这样一个事实:量子电路的状态空间大小是 n 的指数,因此即使对于适中的 n = 50 个量子比特(大约是 Google 实验中使用的数字),状态 |ψ⟩ 也由 250≈1015 个复数描述。因此,在经典计算机上完美模拟量子电路是一个棘手的问题,因此我们假设经典算法具有关于 n 的多项式资源,而不是关于 n 的指数资源。换句话说,从经典计算机获得的样本 Scl 是从实际量子电路的近似值中提取的,当我们增加量子比特的数量时,该近似值不会适当扩展。那么,直观地看,我们可能会认为从经典算法获得的位串与从实际量子电路获得的位串在某种程度上“不同”,因为我们只能粗略地近似电路以获得这些位串。量化这种差异的一个合理方法如下:我们首先问,“如果我对电路的输出状态 | ψ ⟩ 有一个完美的表示,那么我获得样本 S cl 的可能性有多大?”这个概率可以通过计算 | x cl ⟩ 和 | ψ ⟩ 的内积来找到,其中 | ψ ⟩ 表示“完美”的输出状态(即,从完美、无错误的量子计算机的实验实现中获得的输出状态)。然后,我们可以将 Pr(S cl) 与获得量子计算机 Pr(S) 生成的集合 S 的概率进行比较。如果我们为经典算法提供更多资源和/或增加量子电路中的错误率(因此我们的输出状态 | ψ ⟩ 不是“完美”),我们应该看到这些概率相互收敛,因此 Pr( S ) ≈ Pr( S cl )。