XiaoMi-AI文件搜索系统
World File Search System连续
FedDG：通过连续频率空间中的情节学习对医学图像进行分割的联合域概括
联合学习允许分布式的医疗机构可以协作学习具有隐私保护的共享预测模型。在临床部署时，接受联邦学习的模型仍会在联邦外面完全看不见的霍斯群岛上使用时仍会遭受性能下降。在本文中，我们指出并解决了联合域的生成（FedDG）的新型问题设置，该设置旨在从多个分布式源域中学习联合模型，以便它可以直接概括为看不见的目标域。我们提出了一种新颖的方法，在持续频率空间（ELCF）中称为情节学习，通过启动每个客户端在数据分散率的挑战性约束下利用多源数据分布来利用多源数据分布。我们的方法通过有效的连续频率空间插值机制以隐私保护方式传输客户之间的分布信息。通过转移的多源分布，我们进一步仔细设计了面向边界的情节学习范式，以将本地学习暴露于域分布变化，尤其是在医学图像分割场景中尤其满足模型概括的挑战。在两个医学图像分割任务上，我们的方法的有效性优于最先进的表现和深入消融实验。可以在https://github.com/liuquande/feddg-elcfs上使用代码。
数据记录器：连续监视温度计设备
•连续监测和记录•具有液体（甘油或甘油）或松散培养基（玻璃珠或沙子）或固体（Teflon或铝）的缓冲探针。这些缓冲材料测量了小瓶中疫苗的温度，而不是疫苗单元中的气温。•可以从单元外部轻松读取的数字显示•在（+/- 1°F）内（+/- 1°F）（+/-。5°C）精度•显示当前的最低和最大温度读数•最小/最大显示器的重置按钮•至少4,000个记忆存储•至少4,000个读数•至少读取范围读取量•用于范围内的温度•较低的速度速率/较低的速度速度•降低速度•绘制范围•彩色范围•彩色彩色范围<彩色彩电率<彩绘效率<
连续的随机梯度方法：第二部分
摘要在此贡献中，我们提供了对连续的梯度（CSG）方法的数值分析，包括来自拓扑优化和收敛速率的应用。与标准随机梯度优化方案相反，CSG不会从以前的迭代中丢弃旧梯度样品。相反，计算了依赖设计的集成权重以形成凸组合，以作为与当前设计下真正梯度的近似值。随着近似误差在迭代过程中消失，CSG代表了一种混合方法，就像纯粹随机方法一样开始，并且在极限中像完整的梯度方案一样行事。在这项工作中，CSG的效率是针对拓扑优化的实际相关应用的。这些设置的特征是大量的优化变量和一个目标函数，其评估需要以非线性方式串联的多个积分的数值计算。以前无法通过任何现有的优化方法解决此类问题。最后，关于收敛速率，提供了第一个估计值并在数值实验的帮助下确认。
连续的随机梯度方法：第I部分
摘要在此贡献中，我们介绍了连续随机级别（CSG）方法的完整概述，包括收敛结果，步长规则和算法见解。我们考虑了目标函数需要某种形式集成的优化问题，例如预期值。由于通过固定的正交规则近似近似集成可以将人工局部解决方案引入问题，同时同时提高计算工作，因此在这种情况下，随机优化方案变得越来越流行。但是，已知的随机梯度类型方法通常仅限于预期的风险功能，并且本质上需要许多迭代。后者特别有问题，如果评估成本函数涉及求解多个状态方程，例如，以部分差异方程的形式给出。为了克服这些缺点，最近的一篇文章介绍了CSG方法，该方法通过计算依赖设计的集成权重的旧梯度样本信息重复了旧的梯度样本信息，以获得与完整梯度的更好近似值。在原始的CSG纸张收敛中是为了减小的步长而建立的，但在这里，我们提供了CSG的完整收敛分析，用于恒定步长和Armijo-type线路搜索。此外，提出了获得集成权重的新方法，将CSG的应用范围扩展到涉及较高维积分和分布式数据的问题。
对小型非IID批次的无连续学习
机器人视觉是一个领域，不断学习可以发挥重要作用。需要在复杂环境中运行的一种体现的代理，需要经常进行频繁且无法预测的更改才能连续学习和适应。在对象识别的上下文中，例如，机器人应该能够学习（而不忘记）从未见过的类别的对象，并在发现已经知道的班级的新知名度中提高其识别能力。理想情况下，应通过单个对象的简短视频的可用性来触发持续学习，并在线硬件上使用细粒度更新。在本文中，我们引入了一种基于Core50基准的新型持续学习方案，并提出了两种无彩排的连续学习技术CWR*和AR1*，即使在近400个小型非i.i.i.i.i.i.i.i.d的挑战性案例中，也可以有效地学习。增量批处理。尤其是我们的经验表明，在某些情况下，AR1*可以超过15％的精度，均超过15％，在某些情况下，跨培训批次的精确度和恒定的计算和内存开销。
解释了CDK介导的细胞周期控制中的冗余：统一连续性和定量模型
摘要：在真核生物中，Cyclin依赖性激酶（CDKS）是DNA复制和有丝分裂的必需的，并且在整个细胞周期中，依次激活了不同的CDK-循环蛋白复合物。普遍认为，特定的复合物需要遍历G1中细胞周期的承诺，并分别促进S期和有丝分裂。因此，根据一个流行的模型，几十年来一直占据了领域的流行模型，在细胞周期的每个阶段，针对不同底物的独特CDK – cyclin compleces固有的特定座位生成了事件的正确顺序和时间。但是，编码细胞周期蛋白和CDK的基因敲除的结果不支持此模型。通过许多最近的工作验证的替代性“定量”模型表明，CDK活性的总体水平（具有相反的磷酸酶输入）决定了S期和有丝分裂的时间和顺序。我们通过建议将细胞周期分为离散阶段（G0，G1，S，G2和M）的细分被过时且有问题，从而进一步采用了该模型。相反，我们恢复了细胞周期的“连续性”模型，并提出与定量模型的结合更好地定义了理解细胞周期控制的概念框架。
在本报告中 - 连续持有
我们的人民是促使我们前进的关键力量，因为我们迅速改变了能源景观。我们提供了一个充满活力和包容性的工作环境，该环境重视多样性，并为学习，成长和创新提供了充足的机会。今年，我们在总部获得了29.4％的女性代表，超过了我们的目标。尽管传统上，发电项目的女性参与度较低，但我们通过在我们的项目地点雇用两名女性来解决这个问题，从而解决了这一问题。此外，我们继续在我们运营的领域扩大社区的就业机会。迄今为止，我们为658名当地社区成员提供了工作，作为工程师，技术人员和支持人员。为了使我们的员工配备在迅速变化的行业中蓬勃发展所需的技能，我们在报告年度平均提供了每位员工21个小时的培训。
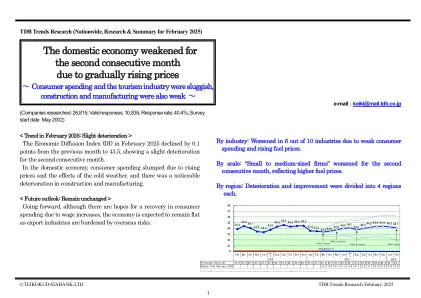
连续第二个国内经济削弱了...
*业务信心（最新在3个月内，在6个月内，在1年内） *业务状况（销售，购买和销售单位价格，库存，库存，容量利用率，员工人数，加班工作时间）3。研究期间和基于互联网的调查2月14日至2825年28 2025年对经济扩散研究的统计研究（启动了经济趋势）的解释（启动了经济统计学趋势） 27,000个全国性公司在其一般业务活动中，包括行业业务绩效和运营环境的当前状况和未来前景。这种调查的主要目的是评估日本经济的现状。选择所有国内行业中各种规模的公司公司都有资格参加调查。
与连续变量的无统治加密
量子信息理论与密码学的婚姻已经引起了一系列规程，这些方案利用了独特的量子现象，最著名的是无关原则[1，2，3]，以实现在经典环境中无法实现的安全性。这样一个概念，即无法统一的加密，可以利用量子状态的不可分割性，以防止对手复制加密消息。术语“无统治加密（UE）”于2003年首次出现在Gottesman [4]的论文中。爱丽丝将经典消息加密到量子状态。引入了一个安全定义，基本上指出“如果鲍勃决定解密有效，那么夏娃，鉴于钥匙，只有关于宣传的信息可忽略不计。”安全定义是根据不同消息的加密之间的痕量距离提出的。在同一框架中，Leermakers和škorić通过钥匙回收设计了UE方案[5]。Broadbent和Lord [6]基于克隆游戏引入了修改的安全定义，并在随机的Oracle模型中构建了UE。在[7、8、9]中引入了几个UE方案，并在[10，11]中给出了UE的可行性和局限性结果。到目前为止，UE已在离散变量（DV）量子系统中专门研究。，在量子密钥分布（QKD）领域，连续变量（CV）量子系统已成为DV的有吸引力的替代品[12、13、14、14、15、15、16、17、18、19、20、21]。在本文中，我们提出了与连续可变状态一起使用的第一个不封合的加密方案。CV不需要昂贵的单光子探测器，并且可以使用低损失的电信波长（1310nm，1550nm）的优势，这使得可以利用数十年的连贯光学通信技术经验。超出QKD，实用的优势更普遍地用于其他量子信息处理应用程序，这引起了人们对将基于DV的加密思想转化为简历域的重大兴趣。我们在[6]的UE框架中提供了安全证明。事实证明，将UE从离散变为连续变量具有许多非平凡方面。在构造方面，需要调整方案的参数，以使得可以满足解密性和不荡情性。在验证技术方面，我们引入了许多“游戏啤酒花”，以将克隆游戏（在UE安全定义中具有特色的克隆游戏）连接到CV一夫一妻制的游戏中，最近证明了获胜概率上的上限[22]。此外，有必要稍微修改
血液神经丝水平预测阿尔茨海默氏病连续体的认知能力下降
1个临床蛋白质的实验室和平台，蒙彼利埃大学，INM Inserm，Irmb Chu de Montpellier，80 AV Fliche，F-34295，法国Montpellier，法国； constance.delaby@inserm.fr 2 Univ。里尔，Inserm，Chu Lille，UMR-S-U1172，Fortile，Lille Neuroscience＆Cognition，Labex Distalz，F-59000 Lille，法国； susanna.schraen@inserm.fr（S.S.-M。）; stephanie.brobois@aphp.fr（S.B.）3巴黎大学，Inserm U1144，GHU APHP中心，Hopital Broca，记忆资源和研究中心德国巴黎 - 布罗卡 - 布罗卡 - 布罗卡 - 德国，F-75013法国巴黎； jean-sebastien.vidal@aphp.fr（J.-S.V.）; olivier.hanon@aphp.fr（O.H.）： +33-（0）4-67-33-71-244斯特拉斯堡大学，斯特拉斯堡大学皮塔利亚大学，记忆资源与研究，法国国家科学中心（CNRS）（CNRS），ICUBE实验室UMR7357和转化型Méticinede Stersbourg（FMTS），Team Multimimimodimodimodimodalimodal inmodal inmodal inmodal Imodal Impodal Impodal Impodal（Ims），F-677 000; ims），F-677 000; f.blanc@unistra.fr 5巴黎大学，INSERM U1144，GHU APHP NORDLARIBOISIèRefernandwidal，认知神经病学中心，法国F-75010，法国巴黎； claire.paquet@aphp.fr 6巴黎大学，精神病学与神经科学研究所，Inserm，UMR-S 1266，F-75014法国巴黎； allinquant.bernadette@neuf.fr 7援助公共 - 帕里斯（AP-HP），DéInteiennede Neurolologie，中心，DES DES DES认知和行为，g piti-pitié-salp（g piti-salp） Neurology，神经病学系INM神经副总监团队，卓越神经退行性疾病中心，法国F-34000 Montpellier； a-gabelle@chu-montpellier.fr 9 Sant Pau存储单元，医院De la Santa Creu I Sant Pau，生物医学研究所Sant Pau，Sant aut Aut aut Aut taut aut taut aut tautaut aut Aut tausitatation：sylvain.lehmann@umontpellier.fr;这样的。