XiaoMi-AI文件搜索系统
World File Search System533 003,安得拉邦,印度 CSE(AI 和 ML)(R23-...
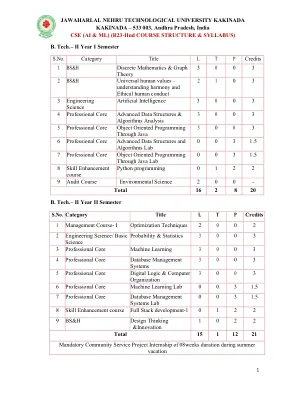
(L1) 第一单元:数理逻辑:命题演算:语句和符号、联结词、合式公式、真值表、同义反复、公式等价性、对偶律、同义反复蕴涵、范式、语句演算的推理理论、前提的一致性、间接证明方法、谓词演算:谓词、谓词逻辑、语句函数、变量和量词、自由和有界变量、谓词演算的推理理论。第二单元:集合论:集合:集合上的运算、包含-排斥原理、关系:性质、运算、分割和覆盖、传递闭包、等价性、兼容性和偏序、哈斯图、函数:双射、组合、逆、排列和递归函数、格及其性质。第三单元:组合学和递归关系:计数基础、排列、重复排列、循环和限制排列、组合、限制组合、二项式和多项式系数和定理。递归关系:生成函数、序列函数、部分分式、计算生成函数系数、递归关系、递归关系公式、通过代换和生成函数解决递归关系、特征根法、解决非齐次递归关系
MoMusic:一种运动驱动的人机协作音乐创作和表演系统
过去几年,人工神经网络架构的重大发展促进了自动音乐创作模型的广泛应用。然而,大多数现有系统都采用基于硬代码和预定义规则的算法生成结构,通常不包括交互式或即兴行为。我们提出了一种基于运动的音乐系统 MoMusic,作为 AI 实时音乐生成系统。MoMusic 具有部分随机谐波排序模型,该模型基于音调和弦进展的概率分析,通过音乐集合论进行数学抽象。该模型针对二维网格呈现,通过姿势识别机制产生结果声音。摄像头捕捉用户手指的运动和轨迹,创造出连贯的、部分即兴的和声进程。MoMusic 集成了多个音色音域,从钢琴等传统古典乐器到使用语音转换技术创建的新型“人声乐器”。我们的研究证明了 MoMusic 的互动性、激发音乐家灵感的能力以及使用各种音色音域生成连贯音乐材料的能力。MoMusic 的功能可以轻松扩展,以结合不同形式的姿势控制音色变换、节奏变换、动态变换甚至数字声音处理技术。
生命、宇宙和一切的答案不是......
第 209-236 页。[2] 安妮·蓝妮克丝,一定有一位天使在抚摸我的心。歌曲。https://www.youtube.com/watch?v=TlGXDy5xFlw。[3] Mohamed S. El Naschie,基于新集合论的量子力学元素及其在高能量子物理和宇宙学中的应用。国际高能物理杂志,24,2017 年,第 65-74 页。[4] 道格拉斯·亚当斯,《银河系漫游指南》。Pan Books。1995 年由威廉·海涅曼首次出版。(特别参见第 104-105 页)。[5] L. Marek-Crnjac:《康托时空理论:与量子纠缠和暗能量有关的空集物理学》。Lambert Academic Publishing,萨尔布吕肯,德国。 ISBN: 978-3-659-12876-9,2013 年。(见 Research Gate 上的摘要)。[6] MS El Naschie,自指称无意义宇宙几何是解决黑洞信息悖论的关键。国际创新与数学杂志,3(5),2015,第 254-256 页。[7] Guo-Cheng Wu 和 Ji-Huan He:论 Menger Urysohn 康托流形理论和物理学中的超限维数。混沌、孤子与分形,42(2),2009,第 781-783 页。[8] Mohamed El Naschie,我们为什么生活在彭罗斯分形无意义非交换多元宇宙中:使用 E-无穷康托时空双射公式的简单证明。国际工程创新与研究杂志,7(5),2018,第 250-253 页。[9] Mohamed S. El Naschie:时空物理学的以太是纯数学的空集。自然科学,9(9),2017,第 289-292 页。[10] MA Helal、L. Marek-Crnjac、Ji-Huan He,MS El Naschie 在 E-
费马大定理在希尔伯特算术中的证明。III.费马大定理与格里森定理的量子信息统一
摘要 。本文的前两部分(分别是 https://philpapers.org/rec/PENFLT-2 和 https://philpapers.org/rec/PENFLT-3)表明,费马最后定理 (FLT) 在希尔伯特算术中的狭义和广义解释可以在第一部分中通过归纳法提出证明,在第二部分中通过 Kochen-Specker 定理提出证明。同样的解释也适用于基于格里森定理的 FLT 证明,部分类似于第二部分中的证明。希尔伯特空间子空间的 (概率) 测度的概念,尤其是其唯一性,可以明确地与偏代数或不可通约性联系起来,或者在广义上解释为希尔伯特算术的两个对偶分支的关系。对最后一个关系的研究使得 FLT 和格里森定理在某种意义上等同于两个对偶对应物,前者可以从后者推出,反之亦然,但需要附加条件,即算术对集合论的哥德尔不完备性。反过来,量子比特希尔伯特空间本身也可以通过 FLT 和格里森定理的统一来解释。利用广义的希尔伯特算术证明 FLT 这样的数论基本结果可以推广到“量子数论”的概念。通过“非标准双射”及其两个与信息论内在关联的对偶分支,可以从数学上研究皮亚诺算术从希尔伯特算术的起源。然后,无穷小分析及其革命性的物理学应用也可以在更广泛的背景下重新实现,例如,作为对时间物理量(分别是物理学中考虑的任何时间过程中的时间导数)出现方式的探索。最后,结果允许对任何层次结构如何产生或改变自身进行哲学反思,这仅归功于其对偶和幂等对应物。关键词:完备性、格里森定理、费马最后定理、希尔伯特算术、幂等性和层次结构、科亨和斯佩克定理、非标准双射、皮亚诺算术、量子信息
约翰·哈丁简历 2024 年 1 月 7 日
约翰·哈丁简历 2024 年 1 月 7 日 约翰·哈丁 办公室电话:(505) 646-4315 数学科学系 系办公室:(505) 646-3901 新墨西哥州立大学 电子邮件:hardingj@nmsu.edu 教育背景: 博士,麦克马斯特大学,1991 年,顾问 G. Bruns 硕士,麦克马斯特大学,1988 年,顾问 G. Bruns 学士,麦克马斯特大学,1987 年 职业经历: 新墨西哥州立大学数学科学系主任,2019 年 – 新墨西哥州立大学正教授,2005 年 – 新墨西哥州立大学副教授,1999 年 – 2005 年 新墨西哥州立大学助理教授,1996 年 – 1999 年 布兰登大学助理教授,1993 年 – 1991 – 1993 教授的课程:微积分 I (191)、II (192)、III (291)、矢量分析 (391)、微分方程 (392)、现代代数简介 (331)、分析(数学 332)、离散数学(278)、有限数学(279)、数学欣赏(数学 210G)、代数 I(581)、代数 II(582)、线性代数(480)、量子计算(530)、格理论(466/506)、组合学(430)、公理集合论(557)、几何基础(452)、通用代数(585)、伟大定理:数学艺术(411)、数理逻辑(454/504)、离散数学(330)、格理论(501)、代数 I(481)、代数 II(482)、高级线性代数(525)、测度论(593)、实分析(594)、计算机科学 I、II(Brandon)、应用统计学(Brandon)、调查抽样(Brandon)、实分析(Brandon)、离散结构和算法(Brandon) 研究生: Miguel Peinado,博士,现任 Jianfeng He,博士,现任 Maria Cruz,博士,伪有序集的完成,2019 年 Taewon Yang,博士,捆绑的逻辑,2015 年 Qin Yang,博士,格的常规完成,2012 年 Barret Church,硕士,Z_2 值状态,2005 年 众多没有论文的硕士生。
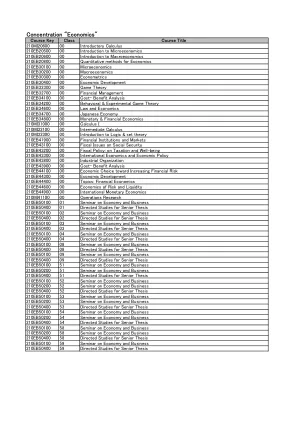
集中“经济学”
课程重点 班级 课程名称 210MI20600 00 微积分入门 210EB20500 00 微观经济学导论 210EB20600 00 宏观经济学导论 210EB20800 00 经济学定量方法 210EB30100 00 微观经济学 210EB30200 00 宏观经济学 210EB30300 00 计量经济学 210EB30400 00 经济发展 210EB32300 00 博弈论 210EB32700 00 财务管理 210EB34100 00 成本效益分析 210EB34200 00 行为与实验博弈论 210EB34600 00 法与经济学 210EB34700 00 日本经济210EB34800 00 货币与金融经济学 210MI31000 00 微积分 I 210MI32100 00 中级微积分 210MI32300 00 逻辑与集合论概论 210EB41900 00 金融机构与市场 210EB43100 00 社会保障财政问题 210EB43200 00 财政政策:税收与福利 210EB43300 00 国际经济与经济政策 210EB43800 00 产业组织 210EB43900 00 成本效益分析 210EB44100 00 金融风险增加的经济选择 210EB44300 00 经济发展 210EB44400 00 主题:金融经济学 210EB44600 00 风险与流动性经济学 210EB44900 00 国际货币经济学 210MI41100 00 运筹学 210EB50100 01 经济与商业研讨会 210EB50400 01 高级论文指导研究 210EB50100 02 经济与商业研讨会 210EB50400 02 高级论文指导研究 210EB50100 03 经济与商业研讨会 210EB50400 03 高级论文指导研究 210EB50100 04 经济与商业研讨会 210EB50400 04 高级论文指导研究 210EB50100 08 经济与商业研讨会 210EB50400 08 指导高级论文研究 210EB50100 09 经济与商业研讨会 210EB50400 09 高级论文指导研究 210EB50100 51 经济与商业研讨会 210EB50200 51 经济与商业研讨会 210EB50400 51 高级论文指导研究 210EB50100 52 经济与商业研讨会 210EB50200 52 经济与商业研讨会 210EB50400 52 高级论文指导研究 210EB50100 53 经济与商业研讨会 210EB50200 53 经济与商业研讨会 210EB50400 53 高级论文指导研究 210EB50100 54 经济与商业研讨会210EB50200 54 经济与商业研讨会 210EB50400 54 高级论文指导研究 210EB50100 58 经济与商业研讨会 210EB50200 58 经济与商业研讨会 210EB50400 58 高级论文指导研究 210EB50100 59 经济与商业研讨会 210EB50400 59 高级论文指导研究
今年(2022 年)诺贝尔物理学奖获奖主题为“纠缠与量子信息:量子力学与科学的新革命”
摘要 . 本文从更广泛、更哲学的角度讨论了今年诺贝尔物理学奖,该奖项旨在表彰纠缠实验“打破贝尔不等式,开创量子信息科学”。该奖项以诺贝尔奖的权威性为“经典”量子力学之外的一个新科学领域赋予了合法性,该领域与泡利的“粒子”能量守恒范式有关,因而也与遵循该范式的标准模型有关。人们认为,最终的未来量子引力理论属于新建立的量子信息科学。纠缠因其严格描述、非幺正性以及非局域和超光速物理信号“幽灵般地”(用爱因斯坦的华丽词藻)同步和传输超距非零作用而涉及非厄米算子,可以被认为是量子引力,而根据广义相对论,它的局域对应物就是爱因斯坦引力,从而开辟了一条不同于标准模型“二次量化”的量子引力替代途径。因此,纠缠实验一旦获得诺贝尔奖,将特别推出以“量子信息科学”为基础的量子引力相关理论,因此被认为是广义量子力学共享框架中的非经典量子力学,它遵循量子信息守恒而不仅仅是能量守恒。宇宙“暗相”的概念自然与已得到充分证实的“暗物质”和“暗能量”相联系,而与经典量子力学和标准模型所固有的“光相”相对立,后者遵循量子信息守恒定律,可逆因果关系或能量与信息的相互转化是有效的。神秘的大爆炸(能量守恒定律普遍成立)将被一种无所不在、无时不在的退相干介质所取代,这种介质将暗相和非局域相转化为光相和局域相。前者只是后者的一个整体形象,事实上它更多地是从宗教而不是科学中借用的。今年的诺贝尔物理学奖预示着一种范式转变,随之而来的是物理、方法论和适当的哲学结论。例如,科学的思维理论也应该起源于宇宙的暗相:可能只是由物理上完全属于光相的神经网络近似地建模。打破泡利范式带来了几个关键的哲学序列:(1)建立了宇宙的“暗”相,与“明”相相对,只有对“暗”相,笛卡尔的“身体”和“精神”二分法才有效;(2)量子信息守恒与暗相相关,进一步将能量守恒推广到明相,有效地允许物理实体“从虚无中”出现,即,来自暗阶段,其中能量和时间彼此不可分割;(3)可逆因果关系是暗阶段所固有的;(4)引力仅从数学上解释:作为有限性对无限性的不完整性的一种解释,例如,遵循关于算术与集合论关系的哥德尔二分法(“要么矛盾,要么不完整性”);(5)层次结构概念仅限于光阶段;(6)在暗阶段,量子的两个物理极端与整个宇宙的可比性遵循量子信息守恒,类似于库萨的尼古拉斯的哲学和神学世界观。关键词:经典量子力学、宇宙的暗相和明相、暗能量和暗物质、爱因斯坦、能量守恒、纠缠、广义相对论、量子力学中的厄米量和非厄米量、局域性和非局域性、泡利粒子范式、量子引力、量子信息、量子信息守恒、量子比特、标准模型、幺正性和非幺正性